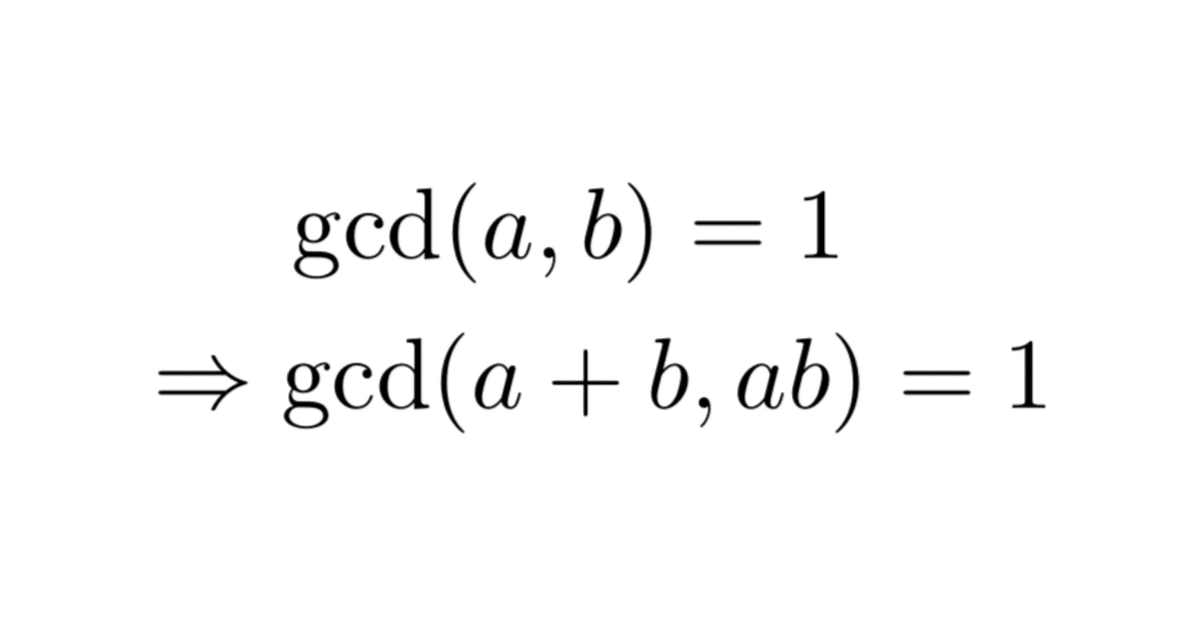
見出し画像

a,bが互いに素⇒a+b,abが互いに素 の証明

大澤裕一

　　　「互いに素な整数$${a,b}$$に対し、$${a+b,ab}$$も互いに素」
の一風変わった証明を紹介します。これについては、素数の性質（整数$${a,b}$$と素数$${p}$$に対し、$${ab}$$が$${p}$$で割り切れるならば、$${a,b}$$の少なくとも一方は$${p}$$の倍数）を用いる方法が有名ですが、今回はこの性質を用いません。

整数論における基本定理「整数$${A,B}$$に対し、$${A,B}$$が互いに素$${\Leftrightarrow}$$[$${Ax+By=1}$$を満たす整数$${x,y}$$が存在する]」を用いています。（$${\Leftarrow}$$は自明ですね）
とてもシンプルですね！


いいなと思ったら応援しよう！