教科を研究する② 　算数編

こんにちは。カリキュラムディレクターの五木田です。前回の蓑手の国語編に続き、算数についてのディスカッションを記録しておこうと思います。

前回の蓑手の記事はこちら

算数といえば

小学校の算数といえば、皆さんは何を思い浮かべるでしょうか。九九の暗記だったり、分数の割り算はなぜかひっくり返して掛け算にすることだったり、時速を割り出すために「みはじ」の公式を覚えたことだったりでしょうか。

算数を学ぶ意味

算数を学ぶ意味は物事を抽象化して考えられるようになることだと考えています。もちろん国語にも、理科にも、社会にも全ての物事に具体と抽象の関係はありますが、算数は特に顕著です。
小学校の算数は目の前のりんごを「1」として捉えることから始まります。低学年でも個数という概念を使って記号化、抽象化が始まります。

（余談ですが、日本の他国の違い・強みで顕著なのは母国語で算数を学べるという点です。他国、特にアメリカは移民が多く、言語をそろえるところに幼少教育の多くの時間を費やします。セミリンガルという言葉がありますが、2ヶ国語以上の言語を有してもどちらも母国語にならない場合、物事を抽象的に捉える・考えることができなくなることがあります。その結果精神年齢が上がらず、精神的な成長が阻害されてしまうこともあるそうです。母国語は思考と成長の根幹を担っています。）

抽象的な理解ができるようになると物事をまとまりとして捉えられるようになります。

まとまりとして捉えられらようになると実際に目の前にないことも想像できたり、操作できるようになります。例えば大きなお金であったり、人口であったり、面積などです。また、実際に行っていないことも比べられるようになります。

算数を学ぶことで想像や理論上の世界を把握する力が身につきます。

ドライな印象を受ける算数、数学の世界ですが、その本質は想像力と密接に関わっていると言えます。

小学校の算数は

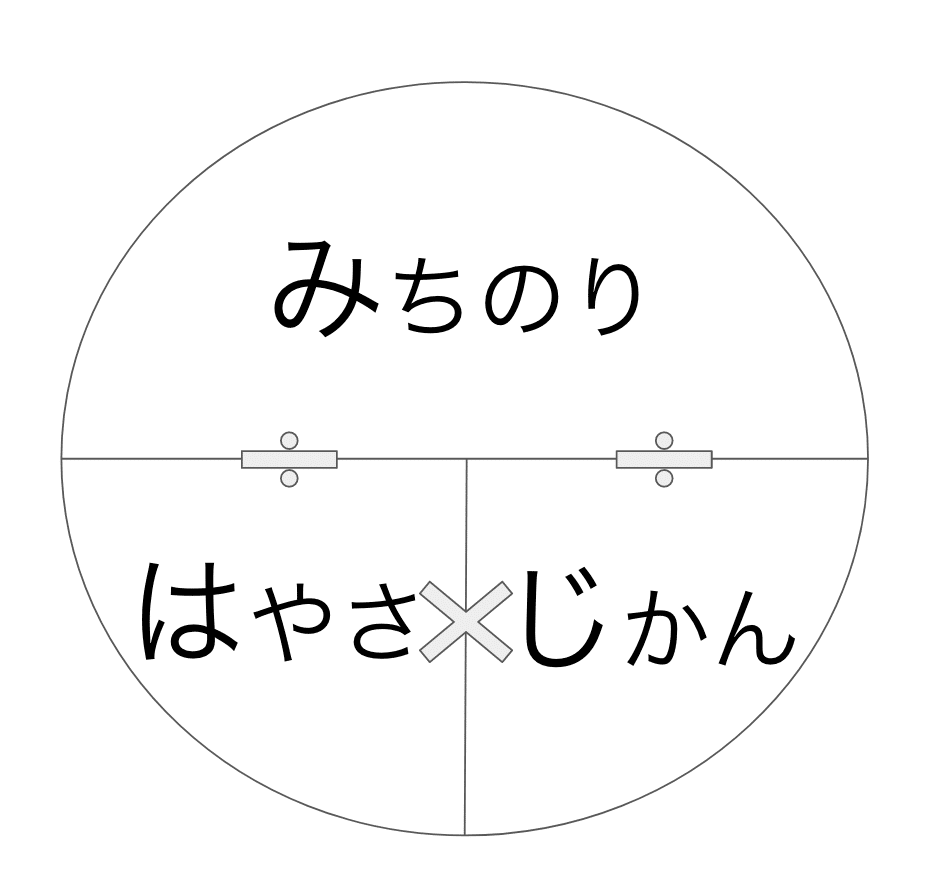
小学校の算数の終着地点は「比」の感覚が身につくかどうかだと考えています（図形はまた違った領域になりますが）。

比の感覚とは、言い換えると「1つあたり」ということがわかっている状態ですです。冒頭に出てきた「みはじ」も「1時間あたりに進む距離（時速）」を元にすれば「みはじの公式」を覚えず原理原則的な理解をすることができます。

冒頭に出てきた「分数の割り算はなぜかひっくり返して掛け算にすること」も方法を暗記するのではなく、原理を理解して考えると説明することができます。たとえば、1÷1/4とはどのような状態でしょう。「分数の割り算はひっくり返して掛け算にする」ことしか覚えていないと、こういった状況をイメージすることができません。

先にも挙げた通り算数の本質は想像力に繋がっています。ここでは仮に1を「1枚のピザ」と考えましょう。

1÷1/4は「1枚のピザに1/4枚のピザが何枚入っていますか？」と言い換えることができます。

つまり、

と説明することができます。

むしろ「分母と分子をひっくり返して掛け算にする」ということを暗記することは学びというより作業に近く、その作業をどれだけ上手くなっても算数・数学の本質とは結びつきません。（それを教えることは否定しません。効率化にもつながるからです。しかし、それ「のみ」に頼った学習法やテストなどは素早く作業ができるようになることであって算数・数学の考えが洗練されているわけではないと考えます。）

HILLOCK初等部では答えだけでなくその中身や過程、本質に着目した学びを大切にしたいと考えています。その感覚をつけるためにも、その感覚をより洗練させていくためにも算数という抽象化されたものを扱う学びは最高の学びの機会になります。

実際にどのようなことを教育活動で扱っていく？

基本的に算数の活動は具体物を入り口として抽象的な発想に導いていきます。

HILLOCKの幼稚園部では隣接した砧公園や林試の森公園、駒沢公園で自然に親しみます。その中で、ある子が「どんぐりを200個集めてみよう！」と言いました。子ども達はどんぐり拾いが大好きです。瞬く間に200個のどんぐりが集まりました。

次はどんぐりを並べます。200個のどんぐりが並んだ様子は壮観です。子ども達は口々に「200個ってこんなに大きい数なんだね」と話します。

幼稚園の段階でも「数」という概念の一端を身近な「どんぐり」という教材から学んでいます。この経験があるかないかで先に挙げたお金や人口などの大きな数の概念の納得感が違います。

高学年になっていくと算数は具体物から離れ、抽象的な世界に入っていきます。先ほど挙げた分数や速さ、割合や確率などがそれに当たります。そして、その先のにある虚数の概念や関数の概念をはじめとした中学校や高校の数学はより抽象的で理論的な世界です。

それらは「目の前に存在しないけれど理論上存在する世界」とも言えるでしょう。ある意味、見えない世界へ想いを馳せる哲学的な側面と目の前の物事を数字と式、論理で表現する工学的な側面の両面あるのが数学です。

国語同様、そのような感覚を得られたら世界の見え方（認知、認識）が変わってきます。目の前にない物事も想像できたり、捉えるようになるからです。インターネットをはじめとした科学技術の進歩で世界は狭くなりましたがその分捉える世界は複雑になりました。そんな世界の中で生きていく子ども達には想像力豊かに、様々な物事に触れていってほしいです。また、我々大人も学習者として様々な物事に触れ世界を広げていけたらと思います。

HILLOCK初等部ではそのような抽象的な領域があることを肌感で理解できるように、時に具体的・実学的に、時に抽象的・学問的に（ワイルド&アカデミック）算数の世界を楽しんでいきます。