数学の小ネタ#14　数値計算の加速法(サンプルプログラム付き)

　無限級数の計算には、多くの繰り返し計算が必要ですが、級数の性質によってはなかなか収束しない厄介な級数も存在します。その中でも交代級数と呼ばれる足し算と引き算が繰り返される級数は、収束が遅いことで知られています。有名な交代級数に円周率の1/4を計算するライプニッツの公式があります。この公式は以下のように、奇数の分母を持つ有理数の足し算と引き算で構成されています。

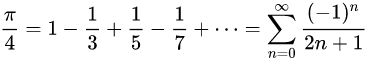
　項数を増やして、この式を素直に計算しても、正解には辿り着きません。例えば1000項まで計算しても、有効数字2桁程度までしか一致しません。こんな時に使われるのが、級数の加速法です。収束を加速する方法には何種類かありますが、ここではオイラー法を紹介します。

　オイラー法の仕組みを言葉で説明するのは難しいのですが、ざっくり言えば、二項展開を利用して元の式を変形して、収束しやすい形にする方法です。詳しいことが知りたい人は、色んな所で紹介されていると思うので、ググってみて下さい。キチンとした専門書で知りたい方には、下記の書籍がお薦めです。

　今回は初の試みとして、参考プログラムを乗せてみました。私はオールドプログラマーなので、数値計算には未だにFortranを使っています。言い訳のように聞こえるかもしれませんが、Fortranしか知らないのではなく、C、BASIC、Pascal、Pythonも使えるうえで、敢えてFortranを使っています^^。

　下記のプログラムは、ライプニッツの公式を使ったπの計算プログラムです。サンプルでは項数を30にしていますが、これで小数点以下14桁ぐらいまで正確に計算できます。これ以上の精度が必要であれば、倍精度ではなく4倍精度を使う必要があります。

!-----------------------------------------
!  Test program for Euler transformation
!  to calculate the value of Pi
!-----------------------------------------
program euler_pi
  Implicit None
  Integer, Parameter :: n=30 
  Integer :: i     
  Real(kind(0d0)) :: fpi, sum1, sum2
  Real(kind(0d0)) :: term, wksp(n)
!
   sum1 = 0.0d0
    Do i = 1, n
      sum1 = sum1 + fpi(i-1)
    End Do
    sum1=4.0d0*sum1
!
    sum2 = 0.0d0
    Do i = 1, n
      term = fpi(i-1)
      Call eulsum(sum2, term, i, wksp)
    End Do
    sum2=4.0d0*sum2
!
    Write (6, *) ' N =', n 
    Write (6, *) ' sum1 =', sum1
    Write (6, *) ' sum2 =', sum2
!
End Program euler_pi
!
function fpi(n)
  implicit none
  integer :: n
  real(kind(0d0)) :: fpi
  fpi=(1.0d0/(2.0d0*n+1.0d0))*(-1.0d0)**n
end function fpi  
!-------------------------
!  Euler transformation
!-------------------------
Subroutine eulsum(ssum, term, jterm, wksp)
  Implicit None
  Integer :: jterm
  Real(kind(0d0)) :: ssum, term, wksp(jterm)
  Integer :: j, nterm
  Real(kind(0d0)) ::  dum, tmp
  Save nterm
!
  If (jterm==1) Then
    nterm = 1
    wksp(1) = term
    ssum = 0.5d0*term
  Else
    tmp = wksp(1)
    wksp(1) = term
    Do j = 1, nterm - 1
      dum = wksp(j+1)
      wksp(j+1) = 0.5d0*(wksp(j)+tmp)
      tmp = dum
    End Do
    wksp(nterm+1) = 0.5d0*(wksp(nterm)+tmp)
    If (abs(wksp(nterm+1))<=abs(wksp(nterm))) Then
      ssum = ssum + 0.5d0*wksp(nterm+1)
      nterm = nterm + 1
    Else
      ssum = ssum + wksp(nterm+1)
    End If
  End If
!
End Subroutine eulsum

数値計算のつぼ