
ミリしら物理探査#24 偏微分方程式
物理探査に限りませんが、物理現象をシミュレートする場合、その物理現象を表わす数学モデルを考える必要があります。複雑な物理現象でも、その基本的な振る舞いは、シンプルな方程式で記述することができます。これらの方程式は、1次元構造などの単純な場合を除けば、偏微分方程式になります。
物理探査の王道である弾性波探査の基礎微分方程式は、波動方程式になります。波動方程式は、波動や振動の現象を表わす方程式で、位相速度s、変位uを使って以下のように表せます。
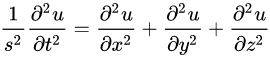
重力探査、磁気探査、電気探査などのポテンシャル論を基礎とする探査法の基礎となるのが、次のポアソン方程式です。この式のφが、重力ポテンシャルや磁気ポテンシャルなどに相当します。また右辺の関数fは、ソース項と呼ばれるもので、重力探査では密度異常、磁気探査では磁気ソース、電気探査では電流源となります。
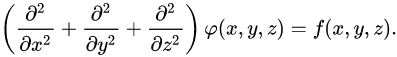
電磁探査や地中レーダ探査の基礎となるのが、以下のマクスウェル方程式です。マクスウェル方程式は一つの式ではなく、電場と磁場の関係が4つの偏微分方程式で表されます。MT法などの電磁探査では、以下の偏微分方程式から出発して、拡散方程式が導かれます。また、地中レーダのような高周波の電磁場を利用する場合には、波動方程式が導かれます。
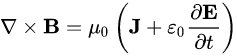
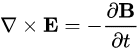
![]()
![]()
これらの方程式を解析的に解くことができるのは、非常に限られた条件の場合だけになります。なので、一般的には数値的にこれらの方程式を解くことになります。このような数値解法で使われるのが、有限要素法(FEM) や有限差分法(FDM)などです。
