
【特集】図解_ファトゥ成分の分類まとめ
※この記事は「日曜数学 Advent Calendar 2024」の参加記事です!(u・∇)v
みなさんこんにちは!今回はファトゥ成分の分類について紹介していこうと思います。
充填ジュリア集合を形作る成分には、色々なものがあります。今回はそれらを詳しく調査し、登場する条件ごとにまとめてみました。
前提知識
本題に入る前に、以下の3つの要素を説明していこうと思います。
・ジュリア集合
・ファトゥ集合とその成分
・充填ジュリア集合
ジュリア集合
ジュリア集合とは、複素関数の反復において、その点から少しでも初期値を動かせば全く違う挙動を示す点の集合のことです。
まず複素関数の反復というものは、複素平面上の点z₀と関数f(z)に対する、zₙ₊₁=f(zₙ)という操作のことです。
例えばz₀=1、f(z)=3z-1とすると、以下のようになります。
z₀=1
z₁=3×1-1=2
z₂=3×2-1=5
z₃=3×5-1=14
z₄=3×14-1=41…
次に、zₙの挙動とはどういうことか説明していきます。f(z)=z²とすると、zₙの変化は3パターンに分類できます。
①無限大に発散する
②0に収束する
③原点を中心とする単位円上を巡回し続ける
例を見ていきます。z₀=3とすると、zₙは9, 81, 6561, 43046721…とものすごい勢いで大きくなっていきます。これはz₀の値を少しずらしてみても、例えば3+0.2iだとか2.8だとかにしてみても変わりません。
また、z₀=0.5iにしてみると、zₙは-0.5, 0.25, 0.0625, 0.00390625…と小さくなっていき、最終的には0に収束していきます。こちらも同様にz₀を0.2+0.5iや0.7iなどにしてみても同じように0に収束します。

zₙ₊₁=zₙ²という反復
ただ、3番だけは少し事情が異なります。
3番に属するz₀の例としてはz₀=1があるのですが、z₀を1から少しずらしただけでも挙動が大きく異なってきます。
z₀=1の場合、zₙはずっと1のままなのですが、これを例えばz₀=0.999とかにするとわずか15回の反復くらいでほとんど0になってしまいます。
以下のグラフは赤がz₀=0.999、青がz₀=1としたときのf(z)=z²の反復です。顕著に差が表れているのがわかると思います。

zₙのnが十分大きければ、1からほんの少し(10⁻¹⁰⁰とか!)でも値をずらすと全く異なる挙動をします。
このように、zₙ₊₁=f(zₙ)という漸化式で、周囲の点との挙動が全く異なる点の集合がジュリア集合なのです。
以降、zₙ₊₁=f(zₙ)という式から生成されるジュリア集合を「f(z)のジュリア集合」と呼ぶことにします。
ファトゥ集合
ファトゥ集合はジュリア集合の補集合、つまりジュリア集合に含まれない全ての点です。
先ほど見たz²という関数であれば、③に属する点はジュリア集合に含まれる、という感じになります。そのため周りと似たような挙動をする①②はジュリア集合に含まれない→ファトゥ集合に含まれる、ということです。
ファトゥ集合の成分というのは、ざっくり言えばこの挙動が何パターンに分類できるか、みたいなことです。z²という関数では普通の発散・普通の収束という2つに分かれましたが、関数を変えると他にも色々なパターンの挙動が見られます。
今回はその挙動たちを探究していくんですね。
充填ジュリア集合
充填ジュリア集合はジュリア集合に似た概念で、zₙ₊₁=f(zₙ)が無限大に発散しないz₀の集合を指します。
例えば、f(z)=z²-0.5+0.5iという関数の充填ジュリア集合は以下のようになります。

黒い領域が充填ジュリア集合に含まれる領域で、外側の領域は充填ジュリア集合に含まれない領域です。
定義上、充填ジュリア集合はファトゥ集合の一部となります。
ジュリア集合というのは、この充填ジュリア集合の境界部分であると言い換えることができます。…が!!!
後に紹介するものには、いくつかの例外が含まれています。とはいえ特殊な場合を除いて、基本的に心配する必要はないと思いますので、ジュリア集合と言われたら「あっ、充填ジュリア集合の境界なんだなぁ」と思っていただければ途中までならなんとかなりますので、ご安心ください。
マンデルブロ集合
マンデルブロ集合は、$${z_{n+1}=z_n^2+c,~z_0=0}$$が無限大に発散しないcの集合です。

今回は発展的な定義として、任意の定数か式aと二変数関数f(z,c)において、$${z_{n+1}=f(z_n,c), z_0=a}$$が無限大に発散しない点の集合を指すことにします。

前提2
どのようなファトゥ成分が登場するのかはジュリア集合の基となる関数で決まります。
定義に出てくるf(z,c)という関数が、以下の4つのうちどれであるかで出現し得る成分が変わります。
・①多項式関数
・②有理関数
・③超越関数
・④非正則関数
今回はこの順番で新しく現れるファトゥ成分を紹介していこうと思います。
また、本題とはそんなに関係ありませんが、ジュリア集合の成分は以下の3つに分けられます。
①反発的不動点
②反発的周期点
③境界上を非周期的に巡回する
例としてはこんなものがあります。
①…f(z)=z²-1においてz₀=φ
φ²-1=φとなる。
②…f(z)=z²+iにおいてz₀=-i
z₁=i²+i=-1+i
z₂=(-1+i)²+i=-2i+i=-i
となり、z₀=z₂となる。
③…f(z)=z²-0.5+0.5iにおいて、適当な境界上の値

このように、ジュリア集合だけでも多くの成分があるのですが、ファトゥ集合の成分はこれよりもさらに面白いものが無数にあります。
ということでようやく本編です。色々なファトゥ成分を解説していきましょう。
多項式関数
多項式関数とは、その名の通り多項式で定義される関数のことです。例えば、$${f(z)=z³+2z²+\frac{1}{3}z+2}$$などが当てはまります。
多項式関数では、以下の四種類のファトゥ成分が見られます。
①発散
②吸引的不動点・周期点
③放物的収束
④ジーゲル円板
順番に見ていきましょう。
発散
まず、①については普通に発散するだけなので特に言うことが無いです。

ただ、物によってはドン引きするレベルで発散が遅いこともあるので油断はできません。
吸引的不動点・周期点
不動点とはzₙ₊₁=zₙとなるような点で、周期kの周期点とはzₙ₊ₖ=zₙとなるような点のことです。
例えば以下の充填ジュリア集合の場合、吸引的な周期点の周期は4となります。

ちなみに、ひとつの充填ジュリア集合に含まれるファトゥ成分の種類は、充填ジュリア集合の基となる関数に依存します。
もとの関数をf(z)とすると、f'(z)=0となる点の数≧吸引的軌道の数になるようです。
例えば、$${\frac{1}{2}z^4-z^2+1.37+0.18i}$$という式は、微分すると2z^3-2z=0となり、解は-1と0のふたつが存在します。
そして、$${\frac{1}{2}z^4-z^2+1.37+0.18i}$$のジュリア集合は以下のようになります。


2種類の吸引的軌道が存在するのがわかります。
ただ、f'(z)=0の解、つまり臨界点が複数存在するからと言って必ず複数の吸引的軌道が現れるわけではなく、いくつかの条件があるようです。
・それぞれの臨界点を初期値としたマンデルブロ集合の重なり合う位置にある
例えば$${\frac{1}{2}z^4-z^2+c}$$の場合、この紫色の範囲に入るcのみ2種類の吸引軌道を持つことができます。

・マンデルブロ集合において、対応する点の周囲の縁がギザギザでない
マンデルブロ集合で対応する点において、このように周囲がガクガクしている部分を初期値に取るとうまくいかないようです。
ただし、今回中央にマンデルブロ集合の形をした領域が存在していますよね。ここをcに取ると、2種類の吸引的軌道を持つ充填ジュリア集合ができます。

マンデルブロ集合型領域の内部の点のひとつ、0.14+0.47iをcとした$${\frac{1}{2}z^4-z^2+0.14+0.47i}$$の充填ジュリア集合を見てみましょう。


しっかりと2種類の吸引的軌道が表れていることがわかりますね。
放物的収束
普通、収束するときはz²+cなら2次関数的に、z³-z²+cなら3次関数的にと、次数に応じて収束のスピードが変化していきますが、特定の条件ではゆっくりと収束していきます。このような軌道を放物的軌道と言い、そのような軌道を持つ充填ジュリア集合を放物型充填ジュリア集合と言います。
z²+cのジュリア集合から、例をいくつか見てみましょう。



はい。まず視覚的特徴として、放物型充填ジュリア集合には谷のような形の領域があることがわかります。
では、これらはどのようにして収束していくのでしょうか?グラフを描いてみましょう。

青はz⁴-z²+0.6875、赤はz²+0.25に対応しています。最終的にはどちらも0.5に収束するはずなのですが、ご覧の通り全く収束速度が異なります。
この赤の方が放物的軌道となっており、その収束の遅さは関数や場合によって変化するものの、指数関数的に遅くなっていくようです。

赤→z²+0.25
とはいえ、このような放物的軌道は他の軌道と比べて圧倒的に収束が遅いため、他とは違う独特な軌道を描いて収束していきます。

ジーゲル円板
充填ジュリア集合内の点が収束する軌道は、不動点や周期点でない、いわば非周期的な軌道になりうるでしょうか?
その答えは真です。特定の条件を満たせば、無限周期と言えるような充填ジュリア集合が生まれるのです。
まずは実例を見ていきましょう。


このように、充填ジュリア集合上の成分で、閉曲線上での無理回転と対応している軌道をジーゲル円板といいます。ここで、無理回転とは以下のような写像のことを言います。

つまりジーゲル円板では、zₙがひとつの点を中心に複素平面上の閉曲線に沿って回転し続けるように動く、ということになります。
面白いことに、ジーゲル円板がどの点を通るのかは初期値によって変化します。場合によっては初期値がそのままジーゲル円板の中に含まれることもあります。

放物的軌道やジーゲル円板を持つ充填ジュリア集合を見つけるには、それと対応するマンデルブロ集合を見ればよいです。
ジュリア集合・ファトゥ集合を生成する式には、何か定数がありますよね。例えばz²+0.25でいうところの(0.25)、z(2-z)(1.3+0.4i)でいうところの(1.3+0.4i)、といった具合です。このような定数をcに置き換えるとマンデルブロ集合の式ができます。z²+cやcz(2-z)といった感じですね。
次に、その式をzについて偏微分し、その零点をaとしてマンデルブロ集合を複素平面上にプロットします。


そうするとこのように円など特定の形がいっぱいくっついたみたいな図形が出てくるので、これらの図形の縁となる点をcとして充填ジュリア集合を選びます。
(多くの場合そのcは無理数となるのですが、中にはキリの良い有理数となる点、すなわち有理点が存在する場合もあります)
このとき、そのcが「図形と図形の接点」であれば放物的軌道を、「接点ではない縁」であればジーゲル円板を持つ充填ジュリア集合が登場しますが、いくつかの注意点があります。
・複数の吸引軌道を持つものと同様、ガタガタの境界部分ではうまくいかない
・aが導関数の零点でない場合、ガクガクした境界が現れ、ジュリア集合との対応が崩れる
さて、ジーゲル円板には通常とは異なる周期の概念が存在します。ジーゲル円板とは閉曲線上を循環する軌道なわけなのですが、その閉曲線の数がジーゲル円板の周期となります。
例えば、z²-0.85+0.2iの充填ジュリア集合の場合、zₙは2つの閉曲線上を往復するような軌道を取るため、周期は2といえます。

また、(0.2+1.1i)(z⁵-z)の場合は4つの閉曲線を通るため、周期は4といえます。

興味深いことに、zₙはそれぞれの閉曲線を順番に循環するようにして動きます。
特定の周期を持つ放物的軌道やジーゲル円板を見つけるには、マンデルブロ集合において対応する周期の部分の縁をcとした充填ジュリア集合を見るとよいです。
例えばこの円い部分は全体的に3周期の周期軌道に収束するので、ここの縁をcとすると3周期の放物的軌道・ジーゲル円板を持つ充填ジュリア集合を見ることができます。



一次元カオス
これは厳密には吸引的不動点・周期点に入るっぽいのですが利便性的にアレなので分けて解説します。
無限周期軌道には閉曲線上以外にも、線上を不規則に巡回するようなものも存在します。

例えばz²-1.5の場合、z₀を実数に取ると、zₙは実軸上を不規則に移動するようになります。

一次元カオスを持つ充填ジュリア集合もマンデルブロ集合から見つけることが可能で、このように直線的に伸びている部分のうち「飛び地」に当たらない地点をcとするとそのような集合が出現します。

ただし、以下の図のように「周りについてる図形」から生えている線の上をcとした場合、線分が曲がって出てくることがあります。


一次元カオスもまた通常とは異なる周期の概念があり、何本の線分上をzₙが暴れ回るかによって決められます。上の図だと4周期ですね。

一次元カオスでも同様に、それぞれの線分を順番に巡回していくようです。
有理関数
有理関数とは、2つの多項式A,Bに対して$${\frac{A}{B}}$$の形で書ける関数です。割り算という動作が増えることにより、より複雑怪奇な動作を見せることがあります。
また有理関数以降はマンデルブロ集合・ファトゥ集合に発散領域が現れないという状態になることもあり、内側を一定の方法で彩色する必要が出ることもあります。
エルマン環
エルマン環はジーゲル円板と似ていますが、一定の範囲より内側を初期値とすると別の軌道に収束するのが特徴です。
例えば、$${\frac{(-0.96+0.28i)(2z^3+5z^2)}{(5z+1)}}$$という関数の充填ジュリア集合にはエルマン環が登場します。

初期値を変えていくと、初めはジーゲル円板のように閉曲線上を非周期的に回転するような軌道を取っていくものの、一定の範囲より内側に入ると0に収束したり、発散したりするようになります。

充填ジュリア集合の内側を、その原点からの距離に応じて彩色すると以下のようになります。グラデーションのところがエルマン環で、真っ白なところが0に収束する領域となります。

エルマン環にもジーゲル円板と同じように、何個の閉曲線を巡回するかで定義される周期の概念があります。お察しの通りこれらも順番に閉曲線を巡っていきますよ。

ちなみに、充填ジュリア集合にエルマン環が登場し得る条件は「関数の次数が3以上であること」らしいです。ここで、次数は既約分数の形になった関数において、分母と分子の次数で大きい方を指します。
エルマン環を簡単に見つける方法は主に2つあります。
・摂動の利用
・一般化ニュートンフラクタルの利用
順番に説明していきます。
まず摂動とは、元の関数に微妙な変化を加えてマンデルブロ集合を少し崩すような操作のことです。
例えば、z²+cという関数に摂動を加えてみましょう。小さな変化ということは、1に近い数を掛けたり値が0に近い項を足したりなどが思いつきますね。今回は$${\frac{z^2(z+n)}{z+m}+c}$$(n≒m)というものを使ってみます。
n=0.5-0.5i、m=0.5-0.49iとして、$${\frac{z^2(z+0.5+0.5i)}{z+0.5+0.49i}+c}$$という関数のマンデルブロ集合を描いてみると以下のようになります。

なんか削れたような領域が確認できますね。そのあたりを拡大してみると、以下のような模様が確認できます。

上部から順に、①円板が並ぶ領域→②砂嵐っぽい領域→③完全に黒い領域と分かれていますが、円板と砂嵐の間にある膜のような部分に注目してほしいです。
エルマン環を見つけるには、この膜状領域にあたる部分の座標をcとしたジュリア集合を描くとよいのです。
実際に描いてみると以下のようになります。エルマン環の特徴が表れていることがわかりますね。

もうひとつの求め方、一般化ニュートンフラクタルを利用するものについて紹介していきます。
$${z_{n+1}=z_n-\frac{f(z_n)}{f'(z_n)}}$$という漸化式は、方程式f(z)=0の解に収束していきます。zがどの解に収束するかはz₀に依存し、どの解に収束するかで複素平面を塗り分けるとフラクタルが登場します。
このような手順でできるフラクタルをニュートンフラクタルと言います。これは定義上有理関数の充填ジュリア集合と見ることができます。
例えば以下はf(z)=z³-1としたニュートンフラクタルです。定義から、$${z-\frac{z^3-1}{3z^2}=\frac{2z^3+1}{3z^2}}$$のファトゥ集合とも表現することができます。この図では以下のような法則で複素平面を塗り分けています。
・1に収束→緑
・$${\frac{1+i\sqrt{3}}{2}}$$に収束→赤
・$${\frac{1-i\sqrt{3}}{2}}$$に収束→青

さて本題はここからです。ニュートンフラクタルのうち、以下の条件を満たすものを見つけます。
・一定の範囲より外側は全て同じ色に塗られる
・それより内側は他の色を含んで塗られる
つまりこんな感じです。これは$${\frac{z^3-1}{z^2+z}}$$のニュートンフラクタルで、この図の外側は全て緑に塗られており→つまり同じzに収束します。
・1に収束→緑
・$${\frac{1+i\sqrt{3}}{2}}$$に収束→赤
・$${\frac{1-i\sqrt{3}}{2}}$$に収束→青

そうしたらこれの一般化ニュートンフラクタルを見ていきます。
$${z-\frac{f(z)}{f'(z)}}$$に対しパラメーターaを加え、$${z-\frac{af(z)}{f'(z)}}$$という式の充填ジュリア集合を一般化ニュートンフラクタルと言います。このときパラメータを|1-a|=1になる点から選ぶとエルマン環を得ることができます。
実際にやってみた結果が以下となります。これはa=1.6+0.8i、$${\frac{z^3-1}{z^2+z}}$$の一般化ニュートンフラクタルで、$${z-\frac{(1.6+0.8i)(z^3-1)(z^2+z)}{z^4+2z^3+2z+1}}$$の充填ジュリア集合と言い換えることができます。
中央のわちゃわちゃしてる部分が環の内側で、その外側のなだらかなグラデーションのところがエルマン環となります。

今あげた2つの方法にはそれぞれメリットとデメリットが存在します。
★摂動のメリット
・2周期以上のものも見つけやすい。
・式を立てやすい。
☆摂動のデメリット
・cがきれいな値になりにくい。
・良い精度のエルマン環を見つけるには非常に高い精度でマンデルブロ集合を描画する必要がある。
❤一般化ニュートンフラクタルのメリット
・cがきれいな値になる。
・必要な性質を満たすニュートンフラクタルを見つけるのは簡単。
♡一般化ニュートンフラクタルのデメリット
・式を立てるのに微分を使用する必要があり、式が長くなりがち。
・2周期以上のものを見つけにくい。
エルマン環を簡単に見つける方法にはそれぞれメリットとデメリットがあるんですね。
周期発散
有理関数からは発散判定も一筋縄ではいかなくなり、外側の彩色法を変えるなど、発散に関わる何かをするとき厄介な状況になることがあります。
例えば、$${\frac{c}{z^2+z}}$$、a=-0.5というマンデルブロ集合を考えてみましょう。

まあ一見普通ですね。では次にzₙがどんな軌道を取って発散するのか見てみましょう。

このグラフを見ると、zₙが0とめっちゃ大きい値を往復しながら発散していき、最終的には0→∞→…というサイクルに漸近するように見えます。
このように、任意の数列Aと∞に対し、A→∞→A→∞→…というサイクルに収束していく場合、外側を滑らかに彩色することができなくなったり、あるいは収束判定に支障を来したりすることがあります。

この図を例にとって説明してみましょう。これは$${\frac{z^4-2}{z^3-1}}$$、つまり$${-\frac{3z^4-8z^3+2}{z^6-4z^3+6z^2}}$$の充填ジュリア集合です。それぞれの点はzₙがどの不動点に収束するかで赤・水・緑・紫に色分けされており、周期点などのどれにも当てはまらない点は黒になるはずです。
ところが、今回は全体が黒であるべき部分、つまり周期発散を示す部分になぜか色がついてしまっています。これは恐らくこの挙動をプログラムが想定していなかったことから起きたのだと思われます。
このように描画に問題を起こす可能性があるため、周期発散に対しては慎重な扱いが必要になってくるのです。
ちなみに、$${\frac{c}{z^2+z}}$$や$${-\frac{3z^4-8z^3+2}{z^6-4z^3+6z^2}}$$は0⇄∞というサイクルに漸近しますが、中には-1→0→∞などといった3周期のものや、同じようにしてできる4周期のものもあります。理論上はいくらでも周期の長いものを作れますよ。理論上は。
こういう文脈での理論上って出来るっちゃ出来るってだけで、実際には到底出来そうもないんですよ。なぁ、あんさん。こういうのでマジでできた例見たことあるか?ないやろ?そういうことや。

👆$${\frac{c+1}{cz^2-z}-1}$$のマンデルブロ集合で、-1→0→∞の3周期発散を示す。
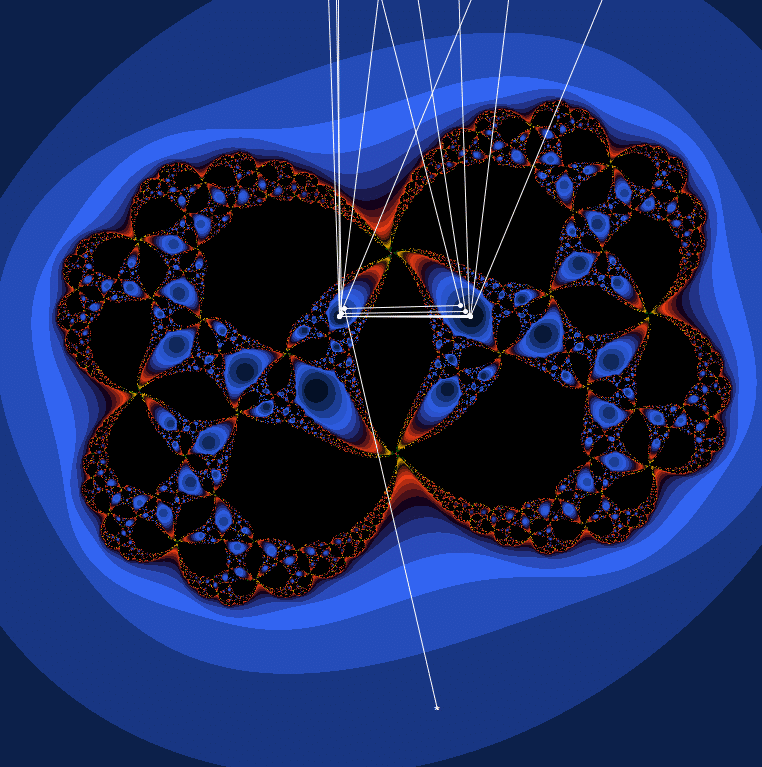
👆c=-0.7+0.33iの時の充填ジュリア集合。
超越関数
超越関数では加減乗除の域を超えて平方根や三角関数、指数や対数なども生成式に取り入れます。そのため値が不連続になったり、発散判定が正常に機能しなくなったりすることがある非常に扱いが難しい式となってしまいますが、それもまた楽しみです。どんなものがあるか見ていきましょう。
ベイカー領域
ベイカー領域と次に紹介するものには、他のファトゥ成分と明確に異なる特性があります。これらの領域を持つジュリア集合は、充填ジュリア集合の縁の部分ではありません。
最初の方に「途中までならジュリア集合の定義はコレで何とかなる」とか言ってましたが、ここからは何とかならなくなるので頑張ってください。
ベイカー領域は「ファトゥ集合内での反復が真性特異点に近づいていくような領域」を指します。
真性特異点とは、関数f(z)において微分不可能かつ、f(z)と$${\frac{1}{f(z)}}$$の極限がいずれも求められないような点のことです。要はヤバい挙動をする点です。
ベイカー領域を持つファトゥ集合には$${f(z)=z+\frac{sin\sqrt{z}}{\sqrt{z}}+a}$$(aは十分大きい正の整数)というものがあります。これの真性特異点は無限遠点のようです。
軌道を取るとこのようになります。

普通の発散と何が違うんだって話ですが、普通に発散する点ではこのようになります。


このように、通常の発散とは異なり反復が真性特異点に近づいていくのがベイカー領域です。
ベイカー領域にも周期の概念があります。例えばこれは0→∞→0→∞→…という2周期のサイクルに近づいていくため、2周期のベイカー領域ということができます。

ところでこの形、どこかで見たことがありませんか?
そうです。周期発散ですね。
ということは、ベイカー領域は真性特異点に近づいていくのに対し、周期発散は極に近づいていく、と見ることができますね。(極とはf(z)は定義できないが1/f(z)は定義できる点のことです)
遊走領域
まず、遊走領域を持つファトゥ集合のひとつ、z+6.4cos(z)のファトゥ集合・ジュリア集合を見てみましょう。

この緑色の部分が遊走領域で、青い部分全体がジュリア集合です。吸引的な不動点や周期点を持たないので、充填ジュリア集合はz=z+6.4cos(z)となる一部の点など(例:$${\frac{\pi}{2}}$$)に限られます。
遊走領域に含まれる点、0をz₀としてzₙの挙動を見てみると、このようになります。

なんか等差数列っぽいですね。それぞれの点の間隔は2πっぽいので、z₀としてzₙ-2πzₙを調べてみましょう。

なんか0.19135355…に近くなっていきそうな雰囲気ですね。もう少し見てみましょう。

あ、なんか出てますね。どうやらzₙ-2πzₙは(周期点か不動点かはこれだけでは判定できませんが)収束していくようです。ということはzₙ自体はどんどん大きくなっていき最後には発散してしまうことになりますね。
このように、以下のような性質を持つ領域を遊走領域と言います。
・それぞれの領域が独立しており、幅のない線でしか繋がっていない
・一度通った領域には反復を重ねても戻らない
・最終的には発散していく
イメージ的にはこんな感じです。

さて、同じく遊走領域を持つファトゥ集合としてz+sin(z)c(cは適切な定数)というものがありますが、その関数のマンデルブロ集合にはこんなものが登場します。

どう見てもアレですね。

なんで急にこれが出てきたのかというと、z+sin(z)cやz+cos(z)cの遊走領域の形はz²+cの充填ジュリア集合の形に酷似しているからです。
まず、これはz+sin(z)(-4.92+0.006i)のファトゥ集合です。

-4.92+0.006iに対応するところはこんな感じになっています。

次に、z²+cのマンデルブロ集合で対応する場所を見て、そこをcとして充填ジュリア集合を描くと…

しっかりと対応する形の充填ジュリア集合が生成されることを確認できました。

さらに面白いことに、遊走領域の軌道が通る点は、充填ジュリア集合上でのzₙが通る点と対応しているのです。
例えば、z-sin(z)+5.1+1.3iというファトゥ集合は以下のようになります。

これはz³+cのマンデルブロ集合で-0.575+0.495i周辺の値に対応しています。-0.575+0.495iの充填ジュリア集合は以下のようになり、似たような形になっていることがわかると思います。
ここで、わかりやすくするため充填ジュリア集合のうち3つの部分に名前を付けようと思います。

この充填ジュリア集合はA→B→C→A→…というサイクルの吸引的軌道を持つのですが、遊走領域上でのzₙの軌道を観察してみると…

遊走領域でも同じようにA→B→C→A→…の順に領域を移動していっていることがわかりますね。
このように、遊走領域上でのzₙの挙動は対応する充填ジュリア集合と同じようになっているんですね。(仕組みは謎です)
非正則関数
非正則関数は一か所でも微分ができない関数のことで、ジュリア集合やファトゥ集合、マンデルブロ集合において大きく特徴が異なってきます。
微分できないのでマンデルブロ集合の適当な初期値を求めることが難しいですが、多くの場合それっぽいのを選べばなんとかなるので大丈夫です。
主な非正則関数にはRe(z)やIm(z)、複素共役(ここではconj(z)で表現します)やabs(z)(ここではabs(Re(z))+i×abs(Im(z))を意味する)などがあげられます。
二次元カオス
非正則関数では一定の範囲内を点が不規則に動き回ることがあります。線上を点が暴れ回るのは見ましたが、今回は二次元の一部範囲を点がカオス的に移動します。
ここでは初期値鋭敏性(初期値が少しでも違えば全く違う軌道を取るようになる)が表れます。
例としてはabs(z)²+0.3-iの充填ジュリア集合が存在します。

ただzₙが通る位置は完全に不規則というわけではなく、通りやすい場所・通りにくい場所・通らない場所が存在するようです。
例えば上のabs(z)²+0.3-iであれば、よくzₙが通るほど濃い色になるよう点の軌道を描くと以下のようになります。

特定の位置をzₙが通りやすいことがわかりますね。
色々な二次元カオスを見ていきましょう。






ベースがどれも似た形になっているのが面白いですね。
ジーゲル円板…??エルマン環…??
ジーゲル円板やエルマン環は本来正則関数、つまり全域で微分可能な関数だけに登場するはずですが、一部の非正則関数にもなぜかジーゲル円板・エルマン環らしきものが登場します。
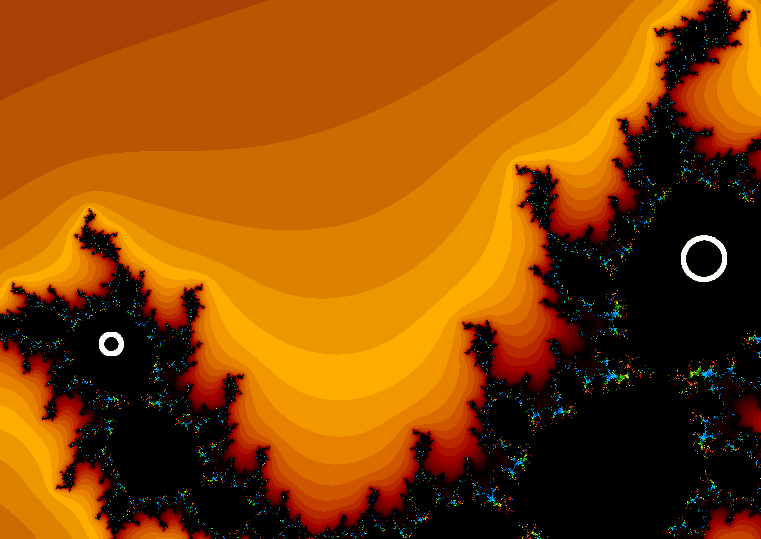

これはconj(z)^2-1+0.098087161717i(近似、正確な値は超越数?)のジュリア集合です。初期値がそのまま環状の軌道に入り、無限周期となっています。
性質上これはジーゲル円板と言えるはずなのですが、ジーゲル円板はどうも正則写像にのみ定義されるようなので、これは謎です。
他にもこんなものがあります。


非正則関数でもマンデルブロ集合の縁を見ることでジーゲル円板…??を探すことができるのですが、注意点がいくつかあります。
まず非正則関数は微分ができないので適切な初期値を求めることができません。なので初期値は充填ジュリア集合をよく観察して適切そうなものを選ぶとよいでしょう。
観察してみて、「充填ジュリア集合が面積を持つとき、その点は必ず充填ジュリア集合に含まれる」という点を見つけたらそれを初期値にします。conj(z²)+cの場合は0ですね。なお、ない場合は諦めて下さい。
次にマンデルブロ集合の縁を見るのですが、ここで「縁の形状」に注目します。
以下の図のように、縁が滑らかな場所では、そこをcにとってもジーゲル円板は登場しません。

以下の図のように、縁がどこまで拡大しても滑らかにならない複雑な場所ではジーゲル円板が登場します。

なお、同じような原理でエルマン環も見つけられないかなと思い試したのですが、残念ながら見つけられませんでした。
ただ、代わりにこのようなものがあります。

どうやら複素共役と$${\frac{a}{z}}$$(aは定数)を組み合わせると、エルマン環っぽい動きをする充填ジュリア集合が出現することがあるようです。



対応するマンデルブロ集合において、以下の図の中央部分のように集中線形の領域が見られる場合、そこを初期値にするとエルマン環…?が得られます。

リミットサイクル
リミットサイクルは閉曲線上を非周期的に巡回しますが、ジーゲル円板とは異なり初期値によって通る点が変化することはありません。
例としてはこんなものがあります。

ジーゲル円板やエルマン環には回転率という概念があり、中央の不動点を中心に閉曲線上を何度(にあたる距離)回転するのかは一定です。つまり、以下の図で示される角度は常に一定になるということです。

ところがリミットサイクルではそのような特性は見られず、場所によって回転角度が変わるようです。

また、リミットサイクルも複数の閉曲線からなる場合もあります。


ただ、リミットサイクルでも同様に、複数の閉曲線をzₙが順番に巡回していく、というのは変わらないようです。
ストレンジアトラクター
ストレンジアトラクターはリミットサイクルと似ていますが、軌道に交叉や初期値鋭敏性が表れ、不規則で複雑な動作が見られます。また二次元カオスとも異なり、点の通る範囲は面状ではなく線状となっています。
以下はストレンジアトラクターの例です。

ストレンジアトラクターにも点が通りやすい・通りにくい場所があります。私のアイコンはz²-Im(2z)+c、a=0のマンデルブロ集合なので、せっかくなのでそこから充填ジュリア集合の例を取りましょう。

これはz²-Im(2z)-0.8-0.5iの充填ジュリア集合とその吸引的軌道です。軌道が見るからに変な形をしていますね。
ストレンジアトラクターを抜き出して描画すると以下のようになります。わずかではありますが通りやすい・通りにくいの傾向がみられますね。

Im(z)²+i×Re(z)×Im(z)-1.86+iの充填ジュリア集合とその軌道を以下に示します。このストレンジアトラクターはzₙの通りやすさの分布が結構はっきりしているものですね。


他にもいくつかストレンジアトラクターを見てみましょう。



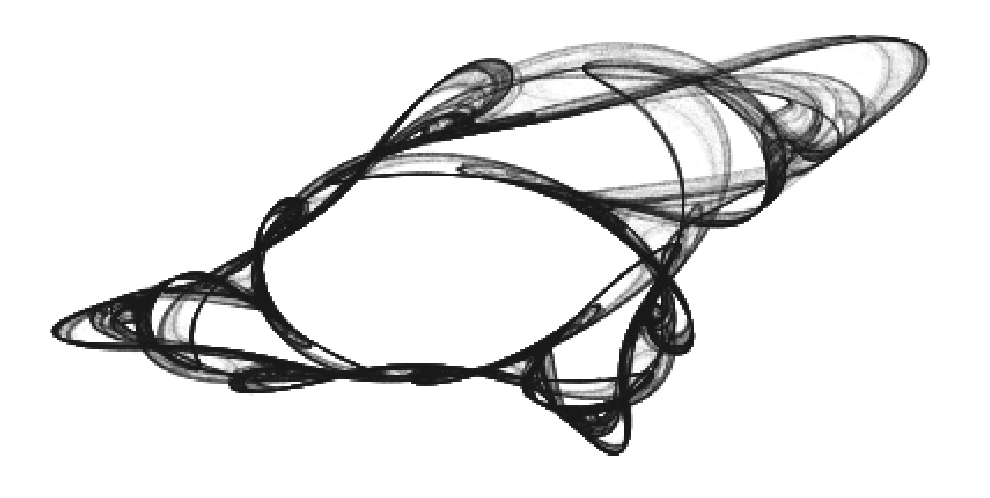


色々な形がありますね。
個人的には、absの入る関数では二次元カオスが、conjの入る関数でジーゲル円板…??が、ReやImの入る関数でリミットサイクルやストレンジアトラクターが多く見られる気がします。
まとめ
というわけでファトゥ成分についてまとめてみました。複素関数を繰り返し適用するだけなのにzₙが様々な動きをするのを観察できて楽しかったですね。式からは予想もできないような、非常に複雑な軌道を見れて面白かったです。
明日の記事はhiromaruさんによる「3乗剰余かl乗和(l:奇素数)について」とのことです。私は整数論も好きなので楽しみです。
参考
宍倉光弘「Surgery of Complex Analytic Dynamical Systems」
Phillip J. Rippon「Baker Domains」
余談
私もしかして日曜数学 Advent Calendar 2024で一番長い記事書いた?(14323文字)
