
シャノン符号化定理(再導出)
今回は独立に記号を発信する情報源の平均符号長が、メッセージが長くなるにつれてエントロピーに近づいていくことを、復号可能性や瞬時復号可能性などの性質を使って導いてみます。前回の議論はこちら:
まず以下の定理を証明します。
シャノン符号化定理
任意の復号可能な符号について

証明の核となるのは対数関数について成立する不等式

です。この不等式の証明は標準的な方法でできます。また等号成立はx=1のときに限ります。さて仮定によって符号は復号可能であるのでKraft-McMillan不等式が成り立ちます。よって

となります。等号成立、つまり情報源のエントロピーと符号の平均符号長とが等しくなるのは、pk = 2^(-dk)のときに限ることがわかります。このときKraft-McMillan不等式においても等式が成り立つことに注意。以上の定理で符号化の能率、すなわち平均符号長は絶対にエントロピーを下回ることはできないことがわかります。
またさらに平均符号長を上から押さえることもできます。すなわち、瞬時復号可能な符号でその平均符号長が
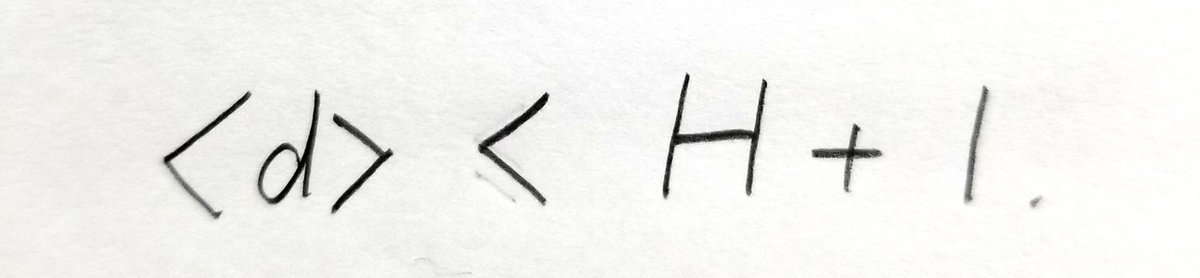
を満たすものが存在することが言えます。ハフマン符号はもちろんこの不等式を満たしています。
証明はすでにシャノンの論文で議論されています。ここでは紹介に留めます。さきほど見たように、pkが2^(-dk)という形で書ければ、これはKraft-McMillan不等式を等号で満たすので、同じdkの組で瞬時復号可能なものが存在します(Kraftの定理)。このときその復号の平均符号長はエントロピーに等しくなっている。確率分布がそうなってはいない一般の場合にも、この特別なケースに近い符号化を模索するというところにアイデアがあります。
具体的にはこうです。まず

を満たすようdkをとってきます。左側の不等式ついてkに関する和をとると、右辺は1となるので、Kraft-McMillan不等式が出てきます。するとこのdkで瞬時復号可能な符号が存在します。また右側の不等式について、両辺の対数をとり、さらにpkを乗じて和をとれば
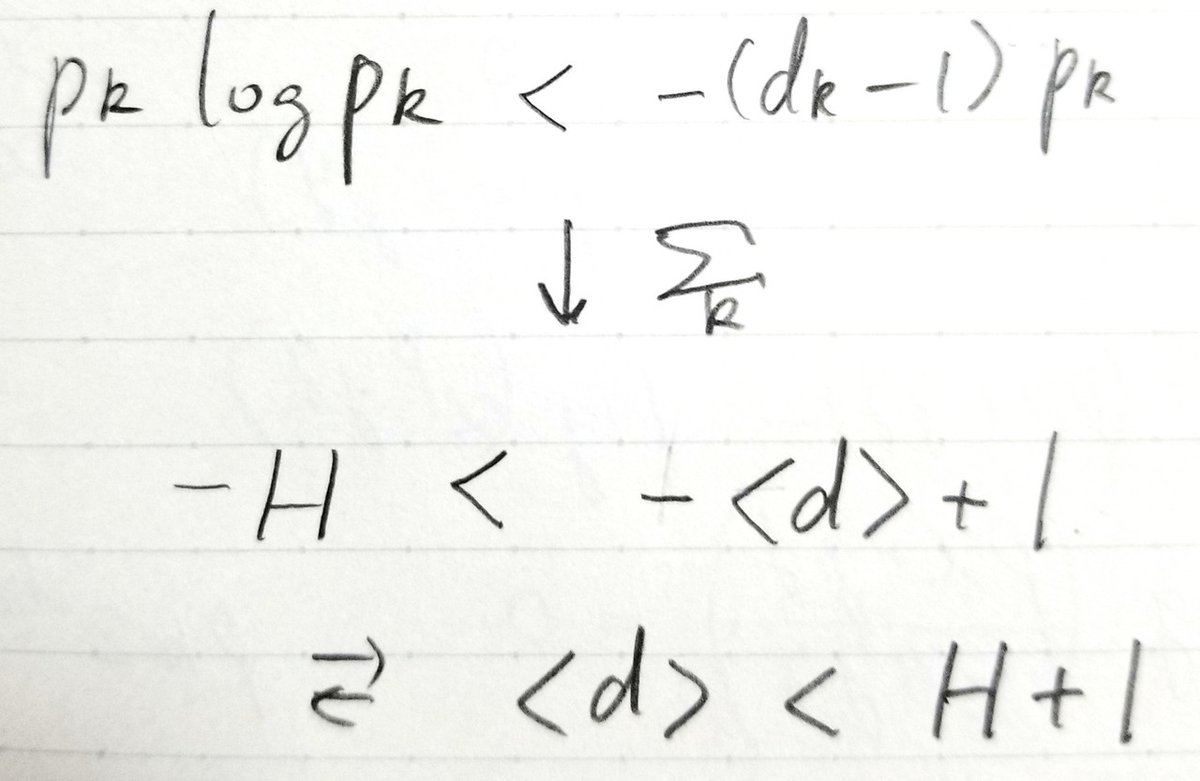
が出てきます。
メッセージ長無限大の極限
次にメッセージが大きくなったときの平均符号長のふるまいを見てみましょう。長さLのメッセージをひとつの記号と見れば、異なる記号がK^L個あり、元の情報源の記号akをnk個含むメッセージが生起する確率は

となります。この確率分布に対応するエントロピーが実はLHであることは以下のようにして示すことができます。まずエントロピーの定義にしたがって書き下すと

となります。多少煩雑ですが、記号に関する和(i, j, k, l)と、nに関する和(αで区別)を分けて表記しています。階乗で表されている係数は、固定されたαに対して、異なるメッセージの総数を表しています。対数の項は真数が積のかたちで表されているので、lに関する和に直すことができます。この和を一番外に出すと

となる。最右端のlog(pk)はlに関する和の直後までくくりだすことができます。ここでさらにαに関する和を二段階で表します。すなわち、まずl番目の記号alの個数nlを0からLのうちからひとつ選んで固定し、その上で足したらL-nlになるようにその他の記号の個数を選びます。このl以外の記号の個数の組をβで区別しましょう。すると上式は

と表せます。ここでnlにしか関係しない項は前に出しました。βに関する和の部分を見ると、恒等式

がそのまま使えます。(ただしL!を(L-nl)!に無理やり変形します。)これを適用して、lを除いたpkの和が1-plに等しいことに注意すれば、

となります。nl=0のときは和に対する寄与もゼロなので、nlの和は1から始めてよいでしょう。このことに注意して

を導きます。すると二項展開の形が現れ、合計がちょうど1となりますので、結局

が出てきます。
長さLのメッセージを新しい記号とみなして得られるこの二次的な情報源に対しても、すでに議論した定理が適用できます。すなわちある瞬時復号可能な符号が存在して、

が成立します。ここでHLや<dL>はこの二次的情報源のエントロピーと平均符号長です。ここにHL=L・Hを用いると、

が示されます。真ん中の項は一記号あたりの符号長と見なせるので、それがLの増大とともにエントロピーに漸近していくことがわかります。
参考文献
[1] クロード・E.シャノン、ワレン・ウィーバー、『通信の数学的理論』、植松友彦訳、ちくま学芸文庫 (2009).
[2] R.G.Gallager, "Information Theory and Reliable Communication" (John Wiley & Sons, New York, 1968).
