相対エントロピー

確率的に起こるイベントが、異なるn個の結果をもつとします。このとき、それぞれの結果が起こる確率は様々に考えることができます。これらの確率に課された制約はただひとつ、規格化条件

ですので、これさえ満たせば(もちろん各pkは非負です)なんでもいいわけです。

いま、n=2とし、確率pで結果aを、確率q=1-pで結果bを次々に、前の結果とは独立に、ある一定のスピードで生起させるイベントの連鎖を考えます。このイベントのエントロピーはもちろん、一記号あたり、

です。ところが実際の観測では、aとbからなる記号の系列は、その時々に応じて、aとbを異なる割合、異なる順序で含むことになります。

そこで、実際に長さNの記号列を観測したとき、そこから実測されたエントロピーH(x)を計算することができます。ここでxは、N個に対するaの個数の割合

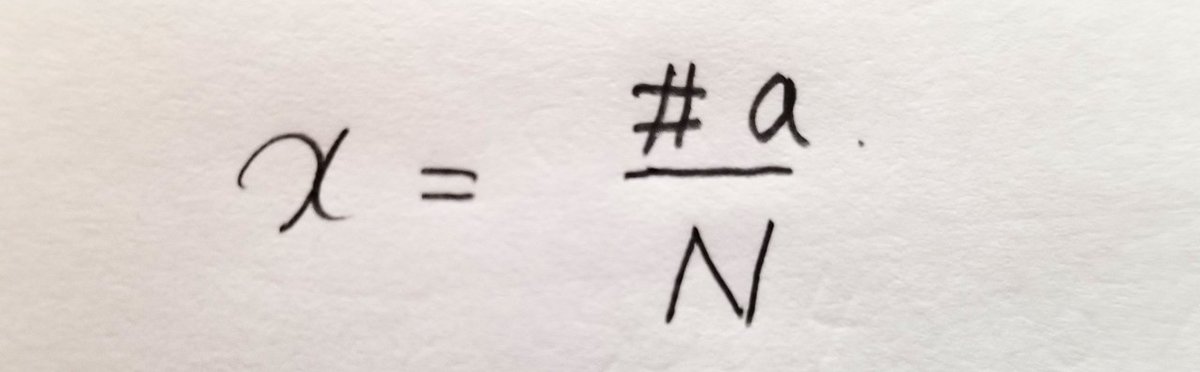
で定義されます。この実測エントロピーと、理論的に計算されるエントロピーH(p)を比較するときに便利なのが相対エントロピーです:

ここでy=1-xです。実測値と理論値が一致するときに限り、相対エントロピーは最小値ゼロをとり、それ以外では正です。この意味で、相対エントロピーは２つの確率分布の近さを定量化したものともいえます。以下、この性質を確認してみます。

相対エントロピーは非負

凸関数の性質を使えば、

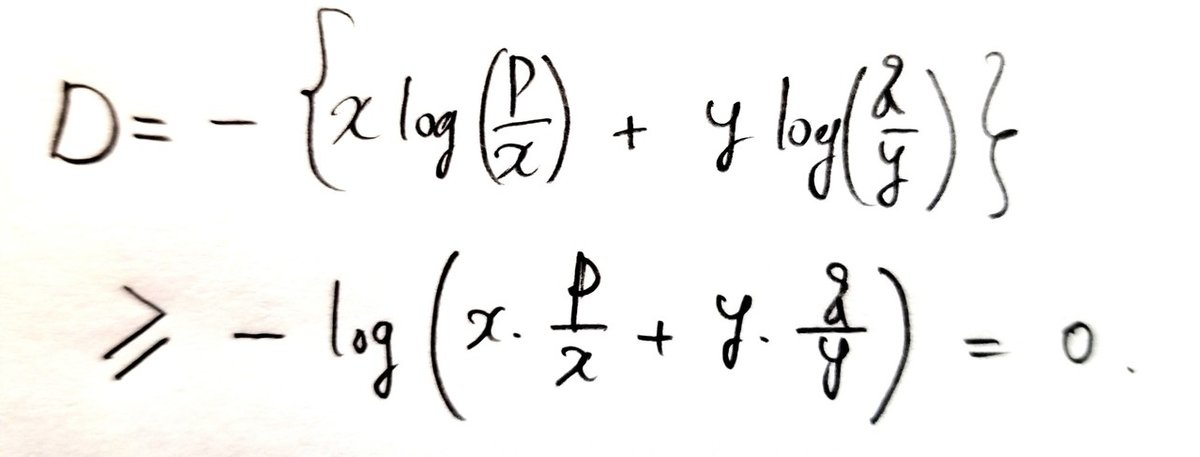
分布が一致のときのみゼロ

ここでは相対エントロピーを変数xの関数と考えます。n変数の一般の場合でも、ラグランジュの未定乗数法によって同様の考え方を適用できます。

相対エントロピーはxの滑らかな関数ですので、極小値をとる点において、関数の傾き(一般のn変数場合は特定の変数に着目したときの偏微分係数)がゼロになることが必要です。実際に計算すると以下のようになります。

逆にx=pであればもちろんD=0ですので、相対エントロピーは確率分布が一致しているときに限り最小値ゼロになることがわかりました。

条件つきエントロピー

多くの確率的イベントでは、次の結果がその前のいくつかの結果の履歴に依存するという性質をもちます。このようなイベントの連鎖をマルコフ連鎖といいます。

数学的に定式化すれば次のようになります。

固定された記号群Sがあり、これはn個の異なる記号からなるとする。いま、ある情報源が単位時間あたりひとつの記号を確率的にSから選んで発信しているとする。情報源は内部状態をもち、これは直近の過去におけるm個の記号の履歴によって定まる。各状態において、情報源がある特定の記号を発信する確率分布がある。

図式化すると以下のようになります。

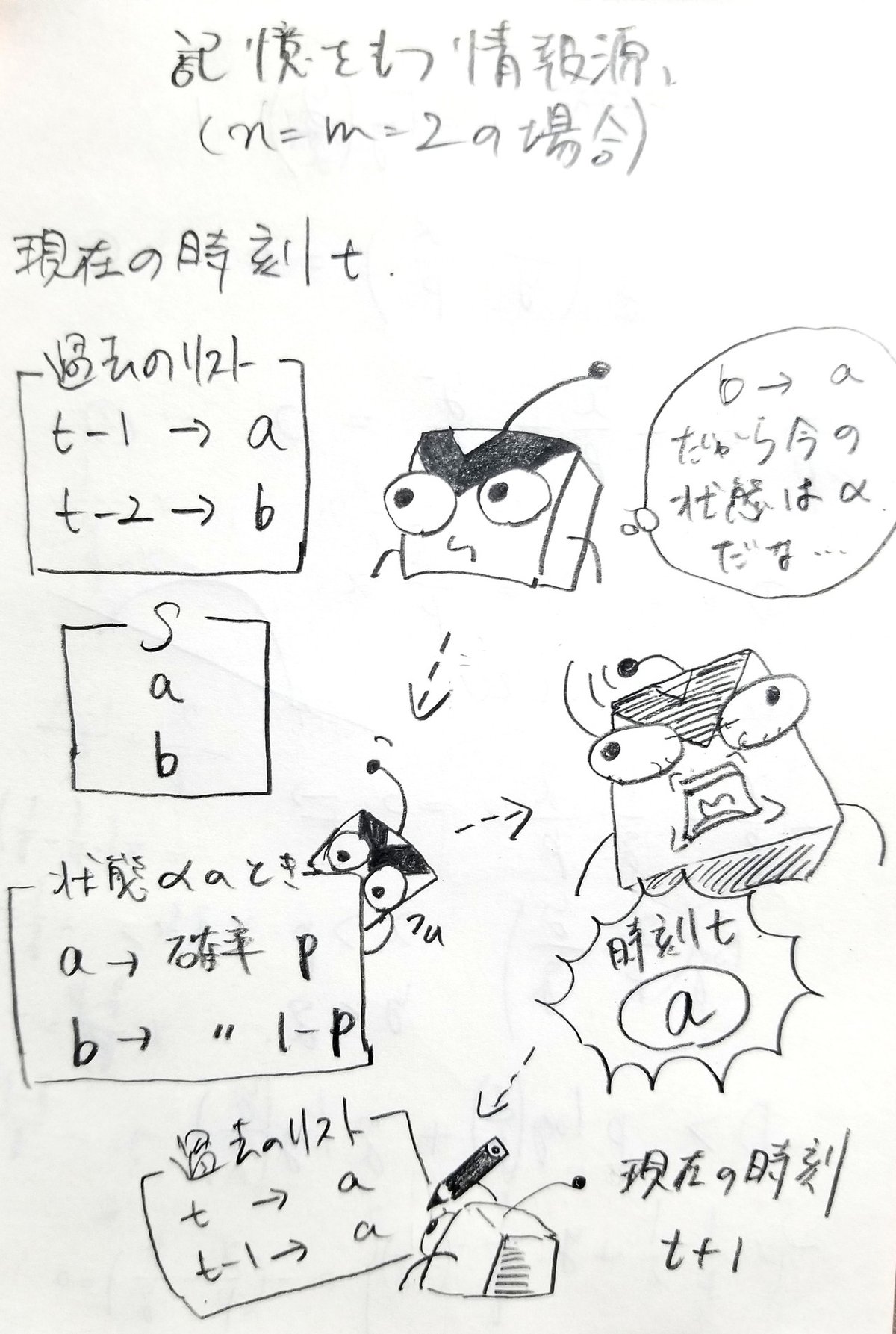
このように確率的に選んだ過去の履歴に応じて状態が遷移し、その状態に依存する確率的分布からひとつの記号を発信、そして更新していきます。

このような情報源に対してもエントロピーと相対エントロピーが定義できます。すなわち、各状態におけるエントロピーを、その状態にいる確率で重み付けして合算すればいいのです。

つまり、状態αにいる確率をP(α)と書けば、条件つきエントロピーは

で、条件つき相対エントロピーは

で定義するのです。ここでpk^(α)は状態αにおいて記号kを発信する確率です。xk^(α)についても同様です。一方、P(α)という確率がうまく定義できるのかについてはいまのところ議論していません。これはマルコフ連鎖のエルゴード性を仮定すると直感的に把握できます。

さて、このエントロピーの概念が、情報源の性質をどのような意味で決定するのか。次回は二状態のマルコフ連鎖などを例にとりつつ、エントロピーの情報理論的意味についてみていきたいと思います。