
Shockley-Queisser Limitを図示しよう
I would be perfectly willing to be shot if I had done wrong
Shockley-Queisser Limitは太陽電池の変換効率の理論限界値を与える。もともとは、Detailed Balance Limitと呼ばれていたが、1961年のJournal of Appplied Physics に掲載された論文の著者であるWilliam ShockleyとHans J. Queisserの 名を取ってSQ Limitと呼ばれるようになった。[1][4]
目的
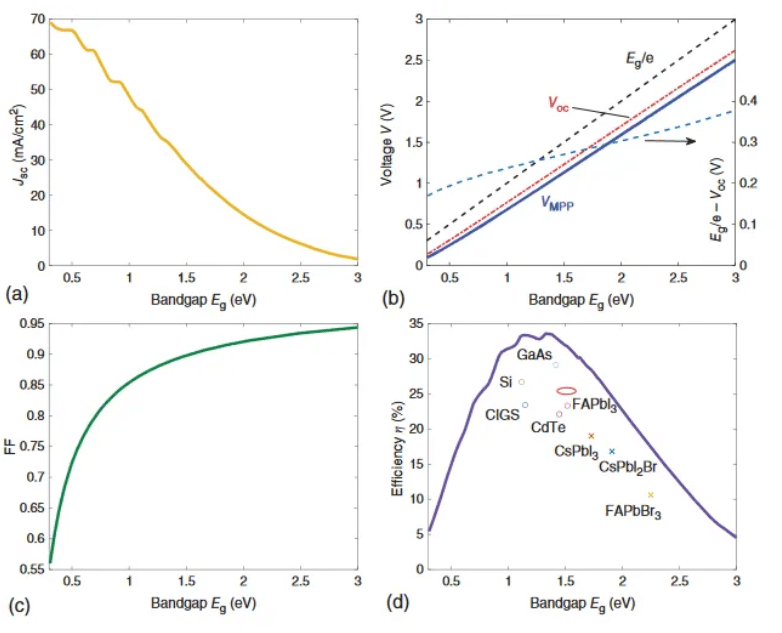
太陽電池に関する研究や文献を読むと、SQ Limit の図(Fig. 1)に頻繁に出くわすことがある。しかし、「この図をどのように描けばよいのか?」と疑問に思う者もいるかもしれない。そこで本記事では、この図を描くことを目標にする。ネット上では、Python を用いて SQ Limit を計算するプログラムが多く見つかる(例えば[5] [6])が、今回は R 言語を使用して同様の計算を行うことにした。
理論背景
ここでは、SQ Limit の背景について簡単に説明する。詳細な理論については参考文献[1] [2] [6]を参照してほしい。
準備
AM 1.5: 太陽光の標準スペクトルであり、通常太陽電池の効率計算に使用される。
エネルギーギャップ($${E_g}$$): 太陽電池の材料が持つバンドギャップエネルギーであり、光を吸収できる最小のエネルギー量を決定する。エネルギーは波長に変換でき、
$${E_g = \frac{hc}{\lambda} = \frac{1240}{\lambda} \text{ (eV)}}$$
の式で表される。ここで、$${E_g}$$ より大きなエネルギーを持つ光子のみが吸収され、それ以外は透過する。
黒体輻射(Black Body Radiation): 黒体はすべての入射光を吸収し、温度に依存した電磁波を放射する。プランクの法則により、黒体が放射するエネルギー密度は次の式で与えられる。
$${B_\lambda(T) = \frac{2hc^2}{\lambda^5} \frac{1}{\exp\left(\frac{hc}{\lambda kT}\right) - 1}}$$
Fig. 2 には、298K における黒体輻射の例を示した。シリコン単結晶(Si-C)は約1.12 eV のバンドギャップを持つため、波長に変換するとおよそ 1100 nm となる。図中の 1100 nm の点線と曲線で囲まれた赤い部分が、シリコンが吸収または放出する光子数を表している
SQ Limitの仮定
SQ Limit では、以下の仮定が置かれる。
太陽電池を黒体として近似する: 太陽電池は、$${E_g}$$ 以上のエネルギーを持つ光を吸収し、輻射再結合によってエネルギーを放出する黒体とみなす。
再結合プロセス: 再結合のプロセスにおいては、輻射再結合(Radiative Recombination: RR)のみを考慮し、オージェ再結合や SRH 再結合は無視する。輻射再結合は、励起された電子が伝導帯から価電子帯に戻る際にバンドギャップエネルギーに対応する光子を放出する現象である。Fig. 2 の赤い部分が輻射再結合に対応する光子の数であり、バンドギャップが大きくなると放出される光子は減少する。

SQ Limitの下での電流密度は以下のように表される。
$${J=J_{SC}-J_0[\exp[\frac{qV}{kT}]-1]}$$
$${J_{SC}}$$:短絡光電流。AM 1.5のスペクトルから求められる。
$${J_{SC}=e\int_{0}^{\lambda_{E_g}}\phi_{solar}(\lambda)d\lambda=e\int_{E_g}^{\infin}\phi_{solar}(E)dE}$$
$${J_0}$$:半導体ダイオードの逆バイアス電流 = 輻射再結合。黒体輻射のスペクトルから求める。
$${J_0=\int_{0}^{\lambda_{E_g}}\frac{2hc^2}{\lambda^5}\frac{1}{\exp[{hc/\lambda kT}]-1}d\lambda=\frac{2\pi}{c^2h^3}\int_{E_g}^{\infin}\frac{E^2dE}{exp(E/(kT))-1}}$$
以下のプログラムでは、AM1.5のスペクトル分布を使用し、短絡電流密度 $${J_{SC}}$$ と 開放端電圧 $${V_{OC}}$$ をバンドギャップに対して求め、それを基に SQ Limit における太陽電池の変換効率(PCE: Power Conversion Efficiency)をバンドギャップに対して図示した。
Rでの実装
準備
ライブラリー、単に等の初期設定を行う。
# Required Libraries
library(readxl)
library(ggplot2)
library(splines)
library(pracma)
# Constants (Approximations where needed)
W <- 1 # Numericalunits equivalent of W (Watt)
K <- 1 # Kelvin
nm <- 1e-9 # Nanometer
m <- 1 # Meter
cm <- 1e-2 # Centimeter
s <- 1 # Second
eV <- 1.60218e-19 # Electron volt
meV <- eV / 1000 # Millielectron volt
V <- 1 # Volt
mA <- 1e-3 # Milliampere
c0 <- 299792458 # Speed of light in m/s
hPlanck <- 6.62607015e-34 # Planck's constant
kB <- 1.380649e-23 # Boltzmann constant
e <- 1.60217662e-19 # Elementary charge
# Cell temperature
Tcell <- 298 * K
MA 1.5のファイルをhttps://www.nrel.gov/grid/solar-resource/spectra-am1.5.htmlからダウンロードする。
*直接ダウンロードしたものを使うとファイルにエラーがあったので、一旦、成型してから使用した。
# Download the Excel file first
file_path<-"C:/Desktop/astmg173.xls"
# Read the downloaded Excel file
worksheet <- read_xls(file_path, col_names = FALSE)
worksheet<- worksheet[-c(1,2),]AM1.5のプロット
worksheetに格納したWavelengthとIntensityの単位を変換する。
# Convert wavelength to nm and intensity to the appropriate units
AM15$Wavelength <- AM15$Wavelength * nm
AM15$Intensity <- AM15$Intensity * W / m^2 / nm
AM1.5のデータを補完し、プロットする。
# Interpolation function
AM15interp <- splinefun(AM15$Wavelength, AM15$Intensity, method = "fmm")
# Define wavelength range and generate the interpolated values
λ_min <- 280*nm
λ_max <- 4000*nm
λs <- seq(λ_min, λ_max, length.out = 500)
y_values <- AM15interp(λs)
# Plot the data
ggplot(data = data.frame(Wavelength = λs / nm, Intensity = y_values / (W/m^2/nm)), aes(x = Wavelength, y = Intensity)) +
geom_line(color="red", size=1.2) + # Red color for the main curve
labs(x = "Wavelength (nm)", y = "Spectral Irradiance (W/m^2/nm)", title = "AM1.5 Solar Spectrum") +
scale_x_continuous(expand = c(0, 0), limits = c(0, 2500)) + # Match the x-axis range to 2000 nm
scale_y_continuous(expand = c(0, 0), limits = c(0, 2), breaks = seq(0, 2, by = 0.5)) + # Adjust the y-axis
theme_classic() + # Clean background
theme(
panel.grid = element_blank(),
axis.text = element_text(size = 15),
axis.title = element_text(size = 15),
plot.title = element_text(hjust = 0.5, size = 22)
) プロットするとFig. 3が得られる。

バンドギャップと吸収される光子数の図示
ここでは、以下の式をプログラムしていき、バンドギャップに対する光子数Sをプロットする。
$${SPhotonsPerTEA=AM1.5 spectrum\frac{1}{E}\frac{hc}{E^2}}$$
$${S =\int_{E_{gap}}^{E_{max}}SPhotonPerTEA (E)dE}$$
$${PowerPerTEA = E*SPhotonsPerTEA(E)}$$
$${Solar constant=\int_{E_{min}}^{E_{max}}PowerPerTEA(E)dE\sim1000 (W/m^2)}$$
#convert in more convenient form
SPhotonsPerTEA <- function(Ephoton) {
λ <- hPlanck * c0 / Ephoton
return(AM15interp(λ) * (1 / Ephoton) * (hPlanck * c0 / Ephoton^2))
}
# Define PowerPerTEA function for integration
PowerPerTEA <- function(E) {
return(E * SPhotonsPerTEA(E))
}
# Integration limits (E_min and E_max)
E_min <- hPlanck*c0/λ_max
E_max <- hPlanck*c0/λ_min
n_points <- 100000
E_values <- seq(E_min, E_max, length.out = n_points)
Power_values <- sapply(E_values, PowerPerTEA)
# calculation of solar constant
solar_constant <- trapz(E_values, Power_values)
print(solar_constant / (W/m^2))
#Integration
solar_photons_above_gap <- function(Egap) {
E_values <- seq(Egap, E_max, length.out = 10000)
SPhotons_values <- sapply(E_values, SPhotonsPerTEA)
result <- trapz(E_values, SPhotons_values)
return(result)
}
# Generate data for the plot (varying bandgap energies)
Egap_list <- seq(0.4*eV, 3*eV, length.out = 100)
y_values <- sapply(Egap_list, solar_photons_above_gap)
#plot
ggplot(data = data.frame(Egap = Egap_list / eV, Photons = y_values / (1e21 * m^-2 * s^-1)),
aes(x = Egap, y = Photons)) +
geom_line(color="red", size=1.2) +
labs(x = "Bandgap energy (eV)",
y = expression(Photons~above~bandgap~(10^{21}~m^{-2}~s^{-1}))) +
theme_classic() +
theme(
panel.grid = element_blank(),
axis.text = element_text(size = 15),
axis.title = element_text(size = 15),
plot.title = element_text(hjust = 0.5, size = 22)
) 
JscとVoc
ここでは、以下の式をプログラムしていく、RR0は輻射再結合であり、黒体輻射の分布から求まる。
$${RR0(E_{gap})=\int_{E_{gap}}^{E_{max}}\frac{2\pi}{c^2h^3}\frac{E^2dE}{exp(E/kT)-1}}$$
$${J(V,E_{gap})=e(S-RR0(E_{gap})(\exp(\frac{eV}{kT})-1))}$$
$${J_{SC}=J(0,Egap)}$$
$${V_{OC}=\frac{kT}{e}\ln\frac{S}{RR0(E_{gap})}}$$
#Radiative Recombination
RR0 <- function(Egap) {
integrand <- function(E) {
E^2 / (exp(E / (kB * Tcell)) - 1)
}
integral <- integrate(integrand, Egap, E_max, subdivisions = 1000)$value
return((2 * pi) / (c0^2 * hPlanck^3) * integral)
}
# J
current_density <- function(voltage, Egap) {
return(e * (solar_photons_above_gap(Egap) - RR0(Egap) *( exp(e * voltage / (kB * Tcell))-1)))
}
# J_SC
JSC <- function(Egap) {
return(current_density(0, Egap))
}
# V_OC
VOC <- function(Egap) {
return((kB * Tcell / e) * log(solar_photons_above_gap(Egap) / RR0(Egap)))
}
# plot of J_SC
Egap_list <- seq(0.4 * eV, 3 * eV, length.out = 100)
JSC_list <- sapply(Egap_list, JSC)
# plot of J_SC
ggplot(data = data.frame(Egap = Egap_list / eV, JSC = JSC_list / (mA / cm^2)),
aes(x = Egap, y = JSC)) +
geom_line(color="red", size=1.2) +
labs(x = "Bandgap energy (eV)",
y = "Ideal short-circuit current (mA/cm^2)",
title = "Ideal short-circuit current as a function of bandgap") +
xlim(0.2, 3) +
ylim(0, 70) +
theme_classic() + # Clean background
theme(
panel.grid = element_blank(),
axis.text = element_text(size = 15),
axis.title = element_text(size = 15),
plot.title = element_text(hjust = 0.5, size = 22)
)
Egap_list <- seq(0.4 * eV, 3 * eV, length.out = 20)
VOC_list <- sapply(Egap_list, VOC)
# Plot of V_OC
ggplot() +
geom_line(aes(x = Egap_list / eV, y = VOC_list / V), color = "red", size=1.2) + # VOCプロット
geom_abline(slope = 1, intercept = 0, linetype = "dashed", color = "black") + # 破線(y=x線)
labs(x = "Bandgap energy (eV)",
y = "Ideal open-circuit voltage (V)",
title = "Ideal open-circuit voltage as a function of bandgap\n(dashed is bandgap)") +
xlim(0.0, 3.5) +ylim(-0.1,3.5)+
theme_classic() + # Clean background
theme(
panel.grid = element_blank(),
axis.text = element_text(size = 15),
axis.title = element_text(size = 15),
plot.title = element_text(hjust = 0.5, size = 22)
)


PCE
P-V関係から、電圧Vを変化させ最大電力点$${V_{mpp}}$$を求める。この$${V_{mpp}}$$を用いて、最大電流$${J_{mpp}}$$と最大電力$${P_{mpp}}$$を計算し、最高変換率PCEを得る。
$${V_{mpp}(E_{gap})=\underset{V}{\max}[ V*J(V,E_{gap})]}$$
$${J_{mpp}(E_{gap})=J(V_{mpp}(E_{gap}), E_{gap})}$$
$${P_{mpp}(E_{gap})=V_{mpp}(E_{gap})*J(V_{mpp}(E_{gap}),E_{gap})}$$
$${\eta(E_{gap})=\frac{maxPower(E_{gap})}{1000 (W/m^2)}}$$
# maximize
fmax <- function(func_to_maximize, initial_guess = 0) {
func_to_minimize <- function(x) {
-func_to_maximize(x) # 最小化関数に変換
}
result <- optim(initial_guess, func_to_minimize, method = "BFGS") # 最適化実行
return(result$par) # 最適化されたパラメータ(最大化されたx)を返す
}
# V_mpp
V_mpp <- function(Egap) {
fmax(function(voltage) {
voltage * current_density(voltage, Egap) # 電力を最大化
})
}
# J_mpp
J_mpp <- function(Egap) {
current_density(V_mpp(Egap), Egap) # 最大電力点の電圧における電流を返す
}
# max_power
max_power <- function(Egap) {
voltage <- V_mpp(Egap)
return(voltage * current_density(voltage, Egap)) # 最大電力
}
# max_efficiency
max_efficiency <- function(Egap) {
return(max_power(Egap) / solar_constant) # 最大電力を太陽定数で割った効率
}
# Egap 1.1eVでの最大効率を計算
eff_1_1 <- max_efficiency(1.1 * eV)
print(eff_1_1)
# Egap_listを0.4eVから3eVの範囲で100個の等間隔の値として生成
Egap_list <- seq(0.4 * eV, 3 * eV, length.out = 100)
# Egap_listに対する効率リストを計算
eff_list <- sapply(Egap_list, max_efficiency)
# プロット
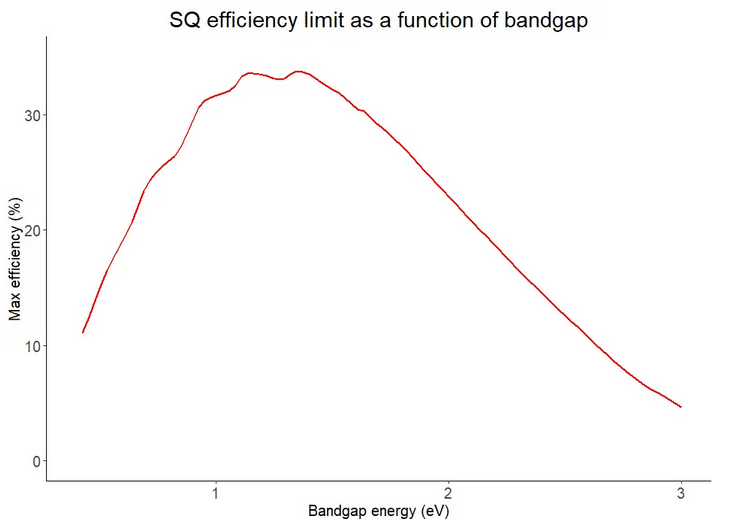
ggplot(data = data.frame(Egap = Egap_list / eV, Efficiency = 100 * eff_list), aes(x = Egap, y = Efficiency)) +
geom_line(color = "red", size=1.0) +
labs(x = "Bandgap energy (eV)",
y = "Max efficiency (%)",
title = "SQ efficiency limit as a function of bandgap") +
xlim(0.4, 3) +
ylim(0, 35) +
theme_classic() + # Clean background
theme(
panel.grid = element_blank(), S
axis.text = element_text(size = 15),
axis.title = element_text(size = 15),
plot.title = element_text(hjust = 0.5, size = 22)
)
バンドギャップが1.1 eVの場合、変換効率が33%と得られる。
参考文献
William Shockley; Hans J. Queisser (March 1961). "Detailed Balance Limit of Efficiency of p-n Junction Solar Cells" (PDF). Journal of Applied Physics. 32 (3): 510–519.
Peter Wurfel, Uli Wurdel (June 2016). "Physics of Solar Cells: From Basic Principles to Advanced Concepts, 3rd Edition". Wiley
Tsutomu Miyasaka (Nvember 2021). "Perovskite Photovoltaics and Optoelectronics: From Fundamentals to Advanced Applications". Wiley.
5.
6.
7.
