オームの法則を図化して理解する

電気回路の比喩

電気回路は、どんなものに喩えられるだろうかと考えると、一般には、管を通る水の流れなどと表現されて、管の面積が小さいと抵抗が大きく・・・、と表現されているようである。わかりやすい。

さらに、電圧とは何か、という話は、位置エネルギーと表現されて、水をポンプアップして高い所に上げて、滝のように落とす、という喩えでわかりやすい。滝のように流れ落ちる際に、電球やモーターの仕事をするのである。

そして、ともに、流れる水の流量が、電流の大きさなのである、と。

では、「抵抗」は管の面積（や周囲の粗度でもよい）というのも理解しやすいが、それらの「電圧」「電流」「抵抗」の3つの関係を表すオームの法則は、どうやって別の言葉や概念で表現できるのだろうか、というところが疑問になった。言い換えると、2次元、または3次元のグラフで表現できないだろうか、という命題が思いついた。

オームの法則の図化

電流、電圧、をそれぞれ直交する軸にとった場合、抵抗は、電圧÷電流なので傾きに相当する概念だろう、というところから、2次元で表現できるのではないかと考えた。しかし、それを考えた2014年頃にはネット検索で探しても、そのことまでを言及したり、実際に2次元で表現したものを、見つけることはできなかった。

表記法1

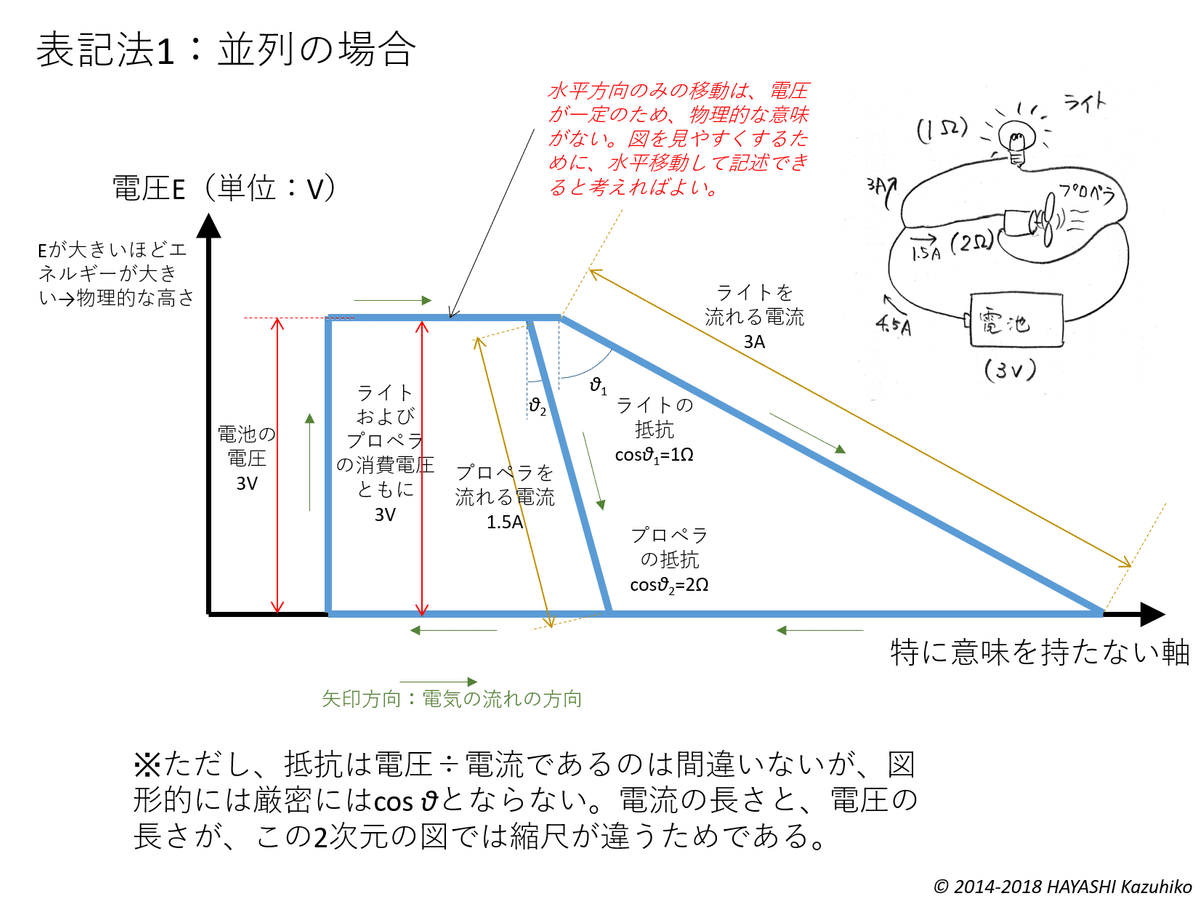
表記法1について説明する。縦軸を電圧にとったのは、水の位置エネルギーが念頭にあるからである。傾きが先にありきであるが、傾きを表すのはsin、cos、tanがよいので、仮にcosとすると、流れる電流の大きさが斜辺の長さに相当するのですっきりする。

抵抗＝傾きであるが、ここでは、抵抗値がcosθとなるため、直接傾きとなっておらず若干わかりにくい。角度が小さい方が抵抗が大きく、角度が大きい方が抵抗が小さくなるので、逆の概念というのがデメリットである。その解釈さえ受け入れれば、図として収まっている。

直流回路の直列回路、並列回路ともに、表現できる。ただし、電流と電圧の大きさの縮尺が同じ場合（ただし単位はA、Vと異なる）には、cosθが正しく抵抗を表しているが、物理的に、三角形の斜辺の長さが一辺の長さよりも短い図形を書くことができないために、ここでは電流の長さが電圧の長さよりも小さい図が書くことができない。そのような場合には、縮尺を変えて下図のように表記せざるを得ない。このとき、見た目の角度と対応していない。角度にこだわらず、cosθ＝斜辺の長さ÷（縦軸方向の）1辺の長さ　と思えば、問題ない。

表記法1：直列の場合

表記法1：並列の場合

表記法2

表記法2は、抵抗＝傾きを感覚的に重視したものである。縦軸が電圧なのはそのままとすると、横軸方向が電流となる。抵抗（図でいうライトやプロペラ）部分の横軸方向の長さが、電流となる。この部分が、若干理解しづらいが、それを受け入れれば、統一的な図が書ける。抵抗の大きさと傾きの大きさが、大小関係も一致して対応している。さらに、表記法1では電流と電圧の大きさの縮尺が変わるケースもあったが、表記法2においては電流の大きさが電圧（の数値）よりも非常に小さくても図が描けるので、グラフの見栄え（扁平）さえこだわらなければ、正確な図が書けて、抵抗値をtanθで表すことができる。グラフの見栄えを調整した場合には、縦横の縮尺が変わるが、表記法1のように、tan θ＝縦方向の長さ÷横方向の長さ　と考えれば、まったく問題がない。

表記法2：直列の場合

表記法2：並列の場合

終わりに

ということで、電気工学が専門でもない素人が知ったかぶりして書いた図であるが、色々なご指摘を受けてさらにブラッシュアップしていきたいと思っている。

私がネットで検索しても、このような図化するものは一切見つけることができなかったが、先人がいれば、それもご指摘いただきたい。

この記事は、私の旧ブログで2018年5月3日に執筆公開した記事の再編集である。