
BitNet&BitNet b158の実装①
はじめに
先週発表された論文『The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits』は多くの人に衝撃を与えたと思います。
それまで量子化とは、有り体に言えば性能を犠牲にメモリ等のコストを抑える手法でした。しかし、BitNet b158(*)では量子化手法としては初めてオリジナルを超える性能を出す可能性を魅せてくれました。
* Githubにある実装名から。以後この記事では名前で元のBitNetとは区別したいと思います。
そんなBitNetとBitNet b158ですが、論文の著者たちからは正式な実験コードが公開されていません。なので、有志の方々が論文を眺めながらあれこれ実装していているのが現状です。
そして、今の所論文の内容を完全に再現できているものはない気がします。(弱々エンジニアの私の理解不足な可能性も大いにありますが。)
むむむ。
— はち (@CurveWeb) March 4, 2024
GithubにあるBitNetもBitNet-Transformersも元の論文と実装違う気がする。
どっちも入力をAbxmax量子化(8bitへの量子化)してないし、BitNet-TransformersはLayerNormないし。
理解が追いついていないだけかな。 pic.twitter.com/WvKWUXcrz1
なので、一旦自身の理解のためにもBitNetの処理やBitNet b158の想像される実装、不明瞭な点を色々な方々の実装をもとに文字に書き起こしていこうと思います。
論文をもとに機能的にコードを考えていく段階であるため最適化されたコードでないことをご了承ください。
また、初めて知る概念等も含まれているため、間違いやそもそもGithubの内容で正しい等あればご意見いただければ幸いです。🙇
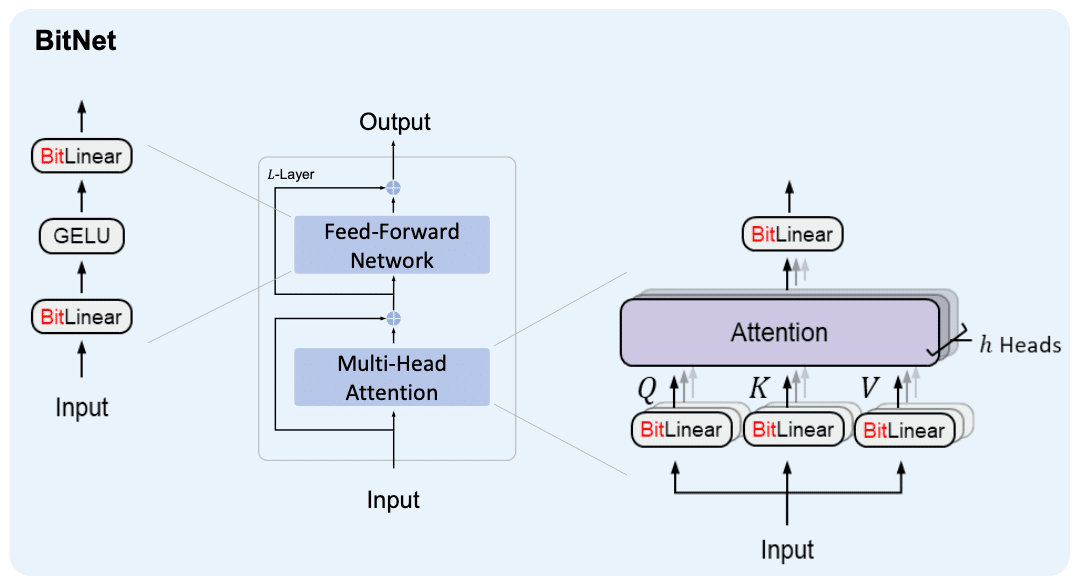
1. BitNet
まずはベースとなるBitNetです。本来はBitNet b158から始めたいですが、BitNet b158の論文にはBitNetとの差分しか書いていないのでBitNetから整理していきます。基本的にはBitLinearだけがBitNetとTransformerの違いなのでBitLinearを見ていきます。
1-1. BitLinearの計算の流れ
BitLinearの処理の流れは以下の通りです。これはBitLinearのforwardを図式化しているのだと思います。
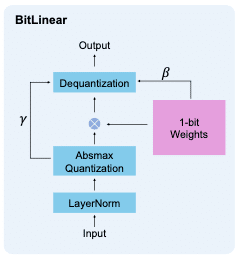
ここから読み取れる処理は大きく分けて5つです。読み取れるinput/outputもなんとなく名前をつけて書いておきます。
LayerNorm (input: x, output: x_norm)
Absmax Quatization (input: x_norm, output: x_q,gamma)
1-bit Weights化 (input: -, output: w_q, beta)
テンソル積(⊗) (input: x_q,w_q, output: x_matmul)
Dequantization (input: x_matmul,beta,gamma, output: output)
ここからではbeta, gammaが何を指すのかわかりませんし、それぞれの処理の中身もこの時点では一部不明です。順番に読み解いていき、実装できるところは以下を埋めていきます。
class BitLinear(nn.Linear):
def __init__(self, in_features, out_features, bias=False):
super(BitLinear, self).__init__(in_features, out_features, bias)
def forward(self, x):
# 1. LayerNorm (input: x, output: x_norm)
# 2. Absmax Quatization (input: x_norm, output: x_q,gamma)
# 3. 1-bit Weights化 (input: -, output: w_q, beta)
# 4. テンソル積(⊗) (input: x_q,gamma, output: x_matmul)
# 5. Dequantization (input: x_matmul,beta,gamma, output: output)
return outputまた、これら計算をまとめて書くと以下の様になる様です。
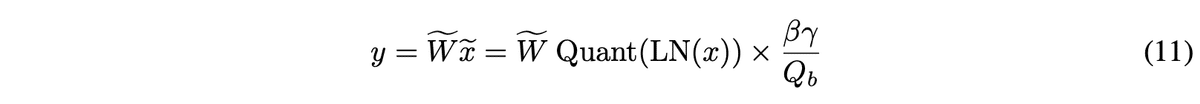
1-2. LayerNorm
To preserve the variance after quantization, we introduce a LayerNorm [BKH16] function before the activation quantization.
とあり、これは一旦通常のLayerNormを用います。実装は以下の様になりそうです。
(オプション1:LayerNormは論文中ではSub-LayerNormという変種を用いています。ただ、別論文の読み込みが必要なため今後の課題とします。)
ここは、BitNet b158に合わせ元のLlama2のRMSNormを使用したいと思います。LlamaRMSNormをそのまま借用すると、以下のようになると思います。
class BitRMSNorm(nn.Module):
def __init__(self, hidden_size, eps=1e-6):
"""
BitRMSNorm is equivalent to LlamaRMSNorm and T5LayerNorm
refers: https://github.com/huggingface/transformers/blob/c5f0288bc7d76f65996586f79f69fba8867a0e67/src/transformers/models/llama/modeling_llama.py#L76C1-L90C59
"""
super().__init__()
self.weight = nn.Parameter(torch.ones(hidden_size))
self.variance_epsilon = eps
def forward(self, hidden_states):
input_dtype = hidden_states.dtype
hidden_states = hidden_states.to(torch.float32)
variance = hidden_states.pow(2).mean(-1, keepdim=True)
hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)
return self.weight * hidden_states.to(input_dtype)class BitLinear(nn.Linear):
def __init__(self, in_features, out_features, bias=False):
super(BitLinear, self).__init__(in_features, out_features, bias, rms_norm_eps=1e-6)
self.layernorm = BitRMSNorm(hidden_size=in_features, eps=rms_norm_eps)
def forward(self, x):
# 1. LayerNorm (input: x, output: x_norm)
x_norm = self.layernorm(x)
# 2. Absmax Quatization (input: x_norm, output: x_q,gamma)
# 3. 1-bit Weights化 (input: -, output: w_q, beta)
# 4. テンソル積(⊗) (input: x_q,w_q, output: x_matmul)
# 5. Dequantization (input: x_matmul,beta,gamma, output: output)
return output式(11)では青枠の部分に当たります。

1-3. Absmax Quatization
We further quantize the activations to b-bit precision. Following [DLBZ22], we use absmax quantization, which scales activations into the range [−Qb, Qb] (Qb = 2**(b−1)) by multiplying with Qb and dividing by the absolute maximum of the input matrix:
xe = Quant(x) = Clip(x × Qb / γ , −Qb + ε, Qb − ε), (4)
Clip(x, a, b) = max(a, min(b, x)), γ = ||x||∞ , (5)
where ε is a small floating-point number that prevents overflow when performing the clipping.
For the activations before the non-linear functions (e.g., ReLU), we scale them into the range [0, Qb ] by subtracting the minimum of the inputs so that all values are non-negative:
xe=Quant(x)=Clip((x−η)×Qb/γ,ε,Qb−ε), η=min_ijx_ij. (6)
ここに関しては、個人的にはわかりづらかったです。(わざと情報をはっきり書いていないのではないかという疑念が湧いてしまいました。)想像で補完したところも含めてしまいますが、見ていきます。
この処理は2パターンに分岐されます。
① 通常、入力xを[-Qb, Qb] の範囲にスケーリングし量子化する(式(4))
② Reluなどの非線形関数の前では、入力xを[0, Qb] の範囲にスケーリングし量子化する(式(6))
この分岐フラグflg_before_linearとすると、この処理absmax_quantize関数は以下の様になります。
def absmax_quantize(self, x):
if self.flg_before_linear:
# パターン①: 通常は[-Qb, Qb]にスケール: 式(4), (5)を適用
else:
# パターン②: Reluなどの非線形関数前の場合は[0, Qb]にスケール: 式(6)を適用
return x_q, gammaBitNetにおいてはGELUの前のBitLinearのみ②の処理になるのではと考えます。(想像補完)
これら①、②共にスケールが違うだけで実施していることはほぼ同じだと思います。①をベースに実施していることを噛み砕いていきます。
基本的に、スケーリング→クリッピング→量子化という流れを踏みます。
スケーリング:
まず、Qb=2**(b-1)によって、情報量が計算されます。ここでは8bitsが採用されているのでQb=128となります。
γ = ||x||∞によって、スケーリングの基準となるγ(gamma)が計算されます。||x||∞はL∞ノルムであり、ベクトルの要素の絶対値の中での最大値を表します。したがって、γ = x.abs().max()で計算されます。これがabsmax量子化におけるabsmax要素になります。
これによって、x / γは[-1, 1]となり、x * Qb / γは[-Qb, Qb]にスケールされます。式(4)中の青枠部分です。

スケーリングの補足として以下の要素が含まれます。
ε(epsilon)はoverflowを防ぐために使われると記載があるため、十分に小さい値を定義します。 ε=1e-6とします。
overflowを防ぐためとあるため、記載はありませんがおそらくx / γをx / (γ+ε)とする必要があるのだと思います。(想像補完)
クリッピング:
Clip(x, a, b)という関数が定義されています。これはxがa≦x≦bとなるように区切ります。(つまり、x<aのときx=aに、x>bの時x=bとします。)これは、pytorchのtorch.clampを用いれば良いと思います。これを用いて[-Qb+ε, Qb-ε]の範囲にクリップします。(正直、なぜこのクリッピングが必要なのかはわかりません。なくても理論的には[-Qb, Qb]になるのでは?と思います。また、x / γをx / (γ+ε)とするためかとも思いましたが、ε>0の時、|x / γ| > |x / (γ+ε)|であるためそれも違うなと思いました。)
スケーリングとクリッピングによって、式(4)を表現することができます。

しかし、式(4)を見るとxが連続値である場合、γ、Qb、εは共にただのスカラー値であるため、これらを計算した結果は連続値となり量子化された値(離散値)とはならない気がします。そのため、最後に以下の要素を付け加えます。
量子化:
torch.roundによる整数化。これによって範囲[-Qb, Qb]の整数という8bits量子化ができると考えます。(想像補完)
これらをabsmax_quantizeに追加すると以下となります。
def absmax_quantize(self, x):
Qb = 2 ** (self.bits - 1)
epsilon = 1e-6 # overflow防止のための小さな値
if self.flg_before_linear:
# パターン①: 通常は[-Qb, Qb]にスケール: 式(4), (5)を適用
gamma = torch.abs(x).max() + epsilon
x_scaled = torch.clamp(x * Qb / gamma, -Qb + epsilon, Qb - epsilon)
else:
# パターン②: Reluなどの非線形関数前の場合は[0, Qb]にスケール: 式(6)を適用
# 論文中の式(4), (5), (6)には記載はないですが、量子化の実施
x_q = torch.round(x_scaled)
return x_q, gamma次に、② Reluなどの非線形関数の前パターンを①との違いをベースに考えていきます。
大きな違いはやはり、入力xを[-Qb, Qb]ではなく[0, Qb]の範囲にスケーリングする点にあります。この違いを以下の要素で生み出します。
スケーリング:
まず、η=x.min()を算出します。η(eta)はxの最小値となるため、x-η ≧ 0となるはずです。
式(4)におけるxをx-η、γをγ-ηと置き換えます。γをγ-ηとするというのは、論文中には記載はないです。ただ、分布がx→x-ηで変化するためスケーリングの基準として使っているγもηを反映した値にすべきだと考えます。(想像補完)これによって、x / γは[-1, 1]であったのが、x-η / γ-ηは[0, 1]にスケールされます。
x-η / γ-η(範囲:[0, 1])にQbをかけることで、[0, Qb]にスケールします。

クリッピング:
その後、x-η / γ-η * Qbとして[0, Qb]となったものを[ε, Qb-ε]の範囲にクリッピングします。

これらによって、入力xを[-Qb, Qb]ではなく[0, Qb]の範囲にスケーリングすることができます。最後は同様にroundで量子化します。
②も含めたabsmax_quantize関数は以下の様になります。
def absmax_quantize(self, x):
epsilon = 1e-6 # overflow防止のための小さな値
if self.flg_before_linear:
# パターン①: 通常は[-Qb, Qb]にスケール: 式(4), (5)を適用
gamma = torch.abs(x).max() + epsilon
x_scaled = torch.clamp(x * self.Qb / gamma, -self.Qb + self.epsilon, self.Qb - epsilon)
else:
# パターン②: Reluなどの非線形関数前の場合は[0, Qb]にスケール: 式(6)を適用
# 論文中には記載はないですが、スケールが異なるためスケーリングの基準として使っているgammaもetaを反映した値にすべきだと考えます。
eta = x.min()
gamma = torch.abs(x - eta).max() + epsilon
x_scaled = torch.clamp((x - eta) * self.Qb / gamma, epsilon, self.Qb - epsilon)
# 論文中の式(4), (5), (6)には記載はないですが、量子化の実施
x_q = torch.round(x_scaled)
return x_q, gamma追加(2024/03/25)
BitNetの論文に公式から追加のFAQがありその中に実装の一部が提示されていました。やはりroundによる量子化は行う必要がある様です。
概ね想像通りの実装ではありましたが、何点か些細な修正を加えます。修正点は以下の3点です。
overflowを防ぐためのγ+εを、γ.clamp(min=ε)
roundとclampの順序の入れ替え
clamp範囲を[-Qb, Qb]から[-Qb, Qb-1]に変更
γ.clamp(min=ε)への変更はεが極小値であるため影響は薄いはずです。
roundとclampは入れ替えによる差は発生しないと思われます。
[-Qb, Qb-1]への変更は量子化した際にint8として扱える様にするためです。ご存知の通りint8は[-128, 127]の範囲を扱います。
この修正を加えたabsmax_quantize関数は以下の通りです。
def absmax_quantize(self, x):
epsilon = 1e-6 # overflow防止のための小さな値
if self.flg_before_linear:
# パターン①: 通常は[-Qb, Qb]にスケール: 式(4), (5)を適用
gamma = torch.abs(x).max().clamp(min=epsilon)
x_scaled = x * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(-self.Qb, self.Qb - 1)
else:
# パターン②: Reluなどの非線形関数前の場合は[0, Qb]にスケール: 式(6)を適用
# 論文中には記載はないですが、スケールが異なるためスケーリングの基準として使っているgammaもetaを反映した値にすべきだと考えます。
eta = x.min()
gamma = torch.abs(x - eta).max().clamp(min=epsilon)
x_scaled = (x - eta) * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(0, self.Qb - 1)
return x_q, gammaこれらを、BitLinearに追加します。Qbは後ほど5. Dequantizationでも使用するためself.Qbとしてinit側に回しました。
class BitLinear(nn.Linear):
def __init__(self, in_features, out_features, bias=False, rms_norm_eps=1e-6, bits=8, flg_before_linear=True):
super(BitLinear, self).__init__(in_features, out_features, bias)
self.layernorm = BitRMSNorm(hidden_size=in_features, eps=rms_norm_eps)
self.bits = bits
self.Qb = 2 ** (self.bits - 1)
self.flg_before_linear = flg_before_linear
def absmax_quantize(self, x):
epsilon = 1e-6 # overflow防止のための小さな値
if self.flg_before_linear:
# パターン①: 通常は[-Qb, Qb]にスケール: 式(4), (5)を適用
gamma = torch.abs(x).max().clamp(min=epsilon)
x_scaled = x * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(-self.Qb, self.Qb - 1)
else:
# パターン②: Reluなどの非線形関数前の場合は[0, Qb]にスケール: 式(6)を適用
# 論文中には記載はないですが、スケールが異なるためスケーリングの基準として使っているgammaもetaを反映した値にすべきだと考えます。
eta = x.min()
gamma = torch.abs(x - eta).max().clamp(min=epsilon)
x_scaled = (x - eta) * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(0, self.Qb - 1)
return x_q, gamma
def forward(self, x):
# 1. LayerNorm (input: x, output: x_norm)
x_norm = self.layernorm(x)
# 2. Absmax Quatization (input: x_norm, output: x_q, gamma)
x_q, gamma = self.absmax_quantize(x_norm)
# 3. 1-bit Weights化 (input: -, output: w_q, beta)
# 4. テンソル積(⊗) (input: x_q,w_q, output: x_matmul)
# 5. Dequantization (input: x_matmul,beta,gamma, output: output)
return output1-2. LayerNorm, 1-3. Absmax Quantizationの処理が式(11)中の青枠部分に当たります。

最後のDequantizationで使うため、absmax_quantize関数はgammaも一緒に返しています。
1-4. 1-bit Weights化
We first binarize the weights to either +1 or −1 with the signum function. Following [LOP+22], we centralize the weights to be zero-mean before binarization to increase the capacity within a limited numerical range. A scaling factor β is used after binarization to reduce the l2 error between the real-valued and the binarized weights. The binarization of a weight W ∈ Rn×m can be formulated as:

順番に見ていきましょう。
α(alpha)は重みWの平均です。Linearはweightをパラメータとして持つので、torch.mean()を使ってその平均を取得すれば良さそうです。
# 式(3): alphaの計算
alpha = self.weight.mean()式(2)にはSign関数が定義されています。torch.sign()を使えば良いと思いきや、torch.sign()は0を0として扱ってしまうので新しくsign関数を定義する必要があります。
custom_sign関数は以下で良さそうです。(x > 0).to(torch.int8)でx>0を1に、x≦0を0にします。その結果にx2 -1を行うことで、x>0を1に、x≦0を-1にします。torch.where()などを用いても実装できますが、こちらの方が処理が速い気がします。(未検証)
# 独自のsign関数の定義
# torch.signは0を0として扱ってしまう。custom_signはW>0を+1に、W≦0を-1とする。
def custom_sign(x):
return (x > 0).to(torch.int8) * 2 - 1最後に、Dequantizationで使うためのβ(beta)をここで計算しておきます。


式(12)によると、βはL1ノルムをweightの要素数で割った値です。これはβ = x.abs().mean()で計算できそうです。
# 式(12): betaの計算
beta = self.weight.abs().mean()βは元々weightを1-bit量子化する際に変化させたスケールをリスケールするために使用されます。(分布[w_low, w_high]→[w_low-α, w_high-α]→[-1, 1]となっていたものを、βをかけることで分布[-β, β]にし、元のスケール[w_low-α, w_high-α]に近づけます。)
これらをBitLinearに追加すると以下の様になります。(custom_sign, quantize_weights関数を追加し、forwardでquantize_weightsを呼び出しています。)
class BitLinear(nn.Linear):
def __init__(self, in_features, out_features, bias=False, rms_norm_eps=1e-6, bits=8, flg_before_linear=True):
super(BitLinear, self).__init__(in_features, out_features, bias)
self.layernorm = BitRMSNorm(hidden_size=in_features, eps=rms_norm_eps)
self.bits = bits
self.Qb = 2 ** (self.bits - 1)
self.flg_before_linear = flg_before_linear
def absmax_quantize(self, x):
epsilon = 1e-6
if self.flg_before_linear:
gamma = torch.abs(x).max().clamp(min=epsilon)
x_scaled = x * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(-self.Qb, self.Qb - 1)
else:
eta = x.min()
gamma = torch.abs(x - eta).max().clamp(min=epsilon)
x_scaled = (x - eta) * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(0, self.Qb - 1)
return x_q, gamma
# 独自のsign関数の定義
# torch.signは0を0として扱ってしまう。custom_signはW>0を+1に、W≦0を-1とする。
def custom_sign(self, x):
return (x > 0).to(torch.int8) * 2 - 1
def quantize_weights(self):
# 式(3): alphaの計算
alpha = self.weight.mean()
# 式(1),(2): 重みの中心化とバイナリ化
weight_binarized = self.custom_sign(self.weight - alpha)
# 式(12): betaの計算
beta = self.weight.abs().mean()
return weight_binarized, beta
def forward(self, x):
# 1. LayerNorm (input: x, output: x_norm)
x_norm = self.layernorm(x)
# 2. Absmax Quatization (input: x_norm, output: x_q, gamma)
x_q, gamma = self.absmax_quantize(x_norm)
# 3. 1-bit Weights化 (input: -, output: w_q, beta)
w_q, beta = self.quantize_weights()
# 4. テンソル積(⊗) (input: x_q,w_q, output: x_matmul)
# 5. Dequantization (input: x_matmul,beta,gamma, output: output)
return outputこれによって、量子化されたWが計算されます。(式(11)青枠)

議論:Wの量子化はinitでしてしまって、BitLiniearはint型で重みを保持するべきかどうか。
これに関しては、はっきりとした記載は論文中になかったと思います。
確かに、毎回量子化の処理を行うのは時間が追加でかかってしまいますし、int型で重みを保持した方がメモリも節約することができます。
しかし、上記のβの計算は量子化されていない値をもとに計算されていることを考えるとBitLinearは少なくとも1bit量子化した値ではない状態で重みを保持していると考えます。それがどの精度で保持しているのかは不明ですが、今回はtorchのLinearを継承しているのでLinearのweight同様のFloat32型で保持するとします。
(オプション2:一方、推論時にはβは変化しないためinitで計算してしまい、重みもinitで量子化するような機構を組み込むべきだと思いますが今回は実施しません。)
1-5. テンソル積(⊗)
With the above quantization equations, the matrix multiplication can be written as:

これは、通常のLinearと同様以下で計算できそうです。
torch.nn.functional.linear(x_q, w_q, self.bias)これをBitLinearのforwardに追加すると以下の様になります。
class BitLinear(nn.Linear):
def __init__(self, in_features, out_features, bias=False, rms_norm_eps=1e-6, bits=8, flg_before_linear=True):
super(BitLinear, self).__init__(in_features, out_features, bias)
self.layernorm = BitRMSNorm(hidden_size=in_features, eps=rms_norm_eps)
self.bits = bits
self.Qb = 2 ** (self.bits - 1)
self.flg_before_linear = flg_before_linear
def absmax_quantize(self, x):
epsilon = 1e-6
if self.flg_before_linear:
gamma = torch.abs(x).max().clamp(min=epsilon)
x_scaled = x * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(-self.Qb, self.Qb - 1)
else:
eta = x.min()
gamma = torch.abs(x - eta).max().clamp(min=epsilon)
x_scaled = (x - eta) * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(0, self.Qb - 1)
return x_q, gamma
def custom_sign(self, x):
return (x > 0).to(torch.int8) * 2 - 1
def quantize_weights(self):
alpha = self.weight.mean()
weight_binarized = self.custom_sign(self.weight - alpha)
beta = self.weight.abs().mean()
return weight_binarized, beta
def forward(self, x):
# 1. LayerNorm (input: x, output: x_norm)
x_norm = self.layernorm(x)
# 2. Absmax Quatization (input: x_norm, output: x_q, gamma)
x_q, gamma = self.absmax_quantize(x_norm)
# 3. 1-bit Weights化 (input: -, output: w_q, beta)
w_q, beta = self.quantize_weights()
# 4. テンソル積(⊗) (input: x_q,w_q, output: x_matmul)
x_matmul = torch.nn.functional.linear(x_q, w_q, self.bias)
# 5. Dequantization (input: x_matmul,beta,gamma, output: output)
return output(オプション3:テンソル積の最適化。w_qが1,-1の2値しか取らないことを利用した最適な積の計算方法がある気がしますが今後の課題とします。)
1-6. Dequantization
The output activations are rescaled with {β, γ} to dequantize them to the original precision.

dequantizationは日本語化すると逆量子化ですが、式(11)を見るとスケールを戻しているだけに見えます。(β, γ, Qb共に既に計算されているスカラー値です。)
したがってこのDequantizationでは、
・weightをw_qに
・xをx_qに
それぞれ量子化した際に変化したスケールを元のスケールに戻す処理を行うものと考えます。(想像補完)
コードは以下の様になりそうです。
output = x_matmul * (beta * gamma / self.Qb)なぜ、x_matmul * (beta * gamma / self.Qb)による再スケーリングが妥当なのでしょうか。そもそも再スケーリングを行う理由は、量子化前(量子化しない全精度時)でのスケールと揃えるためだと思います。
x → x_qとw → w_qでのスケーリングの逆を行う必要があります。そしてそれぞれのスケーリングは以下の通りでした。
x → x_q:x * Qb / γが実施されました。
w → w_q:weight / (weight.abs().max()-weight.mean())が実施されました。(そしてこのスケールはおおよそβ = weight.abs().mean()としても大きくは違わないと思われます。)
したがって、これを使ってx_matmulを再スケーリングすると、x, wが量子化されていないLinearとoutputのスケールが同様になるということなんだと考えられます。
上記をBitLinearに追加した最終型が以下となります。
class BitLinear(nn.Linear):
def __init__(self, in_features, out_features, rms_norm_eps=1e-6, bias=False, bits=8, flg_before_linear=True):
super(BitLinear, self).__init__(in_features, out_features, bias)
self.layernorm = BitRMSNorm(hidden_size=in_features, eps=rms_norm_eps)
self.bits = bits
self.Qb = 2 ** (self.bits - 1)
self.flg_before_linear = flg_before_linear
def absmax_quantize(self, x):
epsilon = 1e-6 # overflow防止のための小さな値
if self.flg_before_linear:
# パターン①: 通常は[-Qb, Qb]にスケール: 式(4), (5)を適用
gamma = torch.abs(x).max().clamp(min=epsilon)
x_scaled = x * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(-self.Qb, self.Qb - 1)
else:
# パターン②: Reluなどの非線形関数前の場合は[0, Qb]にスケール: 式(6)を適用
# 論文中には記載はないですが、スケールが異なるためスケーリングの基準として使っているgammaもetaを反映した値にすべきだと考えます。
eta = x.min()
gamma = torch.abs(x - eta).max().clamp(min=epsilon)
x_scaled = (x - eta) * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(0, self.Qb - 1)
return x_q, gamma
# 独自のsign関数の定義
# torch.signは0を0として扱ってしまう。custom_signはW>0を+1に、W≦0を-1とする。
def custom_sign(self, x):
return (x > 0).to(torch.int8) * 2 - 1
def quantize_weights(self):
# 式(3): alphaの計算
alpha = self.weight.mean()
# 式(1),(2): 重みの中心化とバイナリ化
weight_binarized = self.custom_sign(self.weight - alpha)
# 式(12): betaの計算
beta = self.weight.abs().mean()
return weight_binarized, beta
def forward(self, x):
# 1. LayerNorm (input: x, output: x_norm)
x_norm = self.layernorm(x)
# 2. Absmax Quatization (input: x_norm, output: x_q, gamma)
x_q, gamma = self.absmax_quantize(x_norm)
# 3. 1-bit Weights化 (input: -, output: w_q, beta)
w_q, beta = self.quantize_weights()
# 4. テンソル積(⊗) (input: x_q,w_q, output: x_matmul)
x_matmul = torch.nn.functional.linear(x_q, w_q, self.bias)
# 5. Dequantization (input: x_matmul,beta,gamma, output: output)
output = x_matmul * (beta * gamma / self.Qb)
return output1-7. 他要素(STE)
上記実装によって、論文中の計算フローが実装されました。また、これは式で表すと式(11)に当たります。

しかし、上記BitLinearだけでは推論は可能ですが学習はできません。量子化された値を持つ関数は微分不可能であるため、バックプロパゲーション時にはこの微分不可能な部分をバイパスする必要があります。
このバイパスにはSTE(straight-through estimator)という手法を用います。
STEに関しては以下の図がわかりやすかったです。
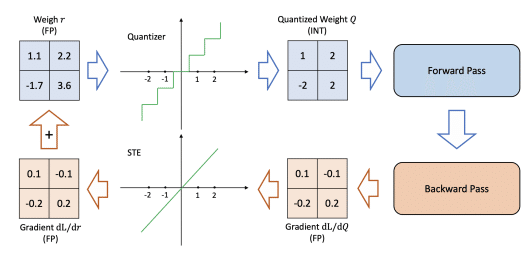
イメージとしては、量子化を行わない状態では下のような関数が、量子化によって上の様な関数となります。それをバックプロパゲーション時には下の関数として扱われるように見せれば良いわけです。
この実装にはTensor.detach()が有用な様です。これは現在の計算グラフから切り離された新しいテンソルを返します。簡単にいうとdetachされた値はバックプロパゲーション時は無視される様です。
これを以下の様に用います。
def calc_and_quantize(x):
x = calc(x) # 何かしらの計算処理
x_q = quan(x) # 量子化処理
return (x_q - x).detach() + xこうすることで、forward時には(x_q - x) + x、つまりx_qが利用されます。そして、backward時には(x_q - x)部分が無視されてxのみが利用されます。これによってbackward時には量子化処理が行われていないように扱われます。
現状、BitLinearではabsmax_quantize, quantize_weights関数で量子化が行われています。そこにSTEを使います。すると以下の様になると思います。
def absmax_quantize(self, x):
epsilon = 1e-6 # overflow防止のための小さな値
if self.flg_before_linear:
# パターン①: 通常は[-Qb, Qb]にスケール: 式(4), (5)を適用
gamma = torch.abs(x).max().clamp(min=epsilon)
x_scaled = x * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(-self.Qb, self.Qb - 1)
else:
# パターン②: Reluなどの非線形関数前の場合は[0, Qb]にスケール: 式(6)を適用
# 論文中には記載はないですが、スケールが異なるためスケーリングの基準として使っているgammaもetaを反映した値にすべきだと考えます。
eta = x.min()
gamma = torch.abs(x - eta).max().clamp(min=epsilon)
x_scaled = (x - eta) * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(0, self.Qb - 1)
# STE
x_q = (x_q - x_scaled).detach() + x_scaled
return x_q, gammadef quantize_weights(self):
# 式(3): alphaの計算
alpha = self.weight.mean()
# 式(1),(2): 重みの中心化とバイナリ化
weight_centered = self.weight - alpha
weight_binarized = self.custom_sign(weight_centered)
# 式(12): betaの計算
beta = self.weight.abs().mean()
# STE (weight_binarizedとスケールを合わせるためweight_centered /betaとしています。)
weight_centered = weight_centered / beta
weight_binarized = (weight_binarized - weight_centered).detach() + weight_centered
return weight_binarized, betaバイパスの前後でスケールがほぼ同じとなるように、weight_centeredはweight_centered.abs().max()で割っています。また、この際overflow防止のためにepsilonを分母に足します。そのため、epsilonをabsmax_quantizeから外出ししてBitLinearのパラメータとします。
STEについては以下の記事に調べた詳細をまとめているのでご参照いただければと思います。
これによってBitLinearは以下の様になります。
import torch
from torch import nn
class BitLinear(nn.Linear):
def __init__(self, in_features, out_features, bias=False, rms_norm_eps=1e-6, bits=8, flg_before_linear=True):
super(BitLinear, self).__init__(in_features, out_features, bias)
self.layernorm = BitRMSNorm(hidden_size=in_features, eps=rms_norm_eps)
self.bits = bits
self.Qb = 2 ** (self.bits - 1)
self.flg_before_linear = flg_before_linear
self.epsilon = 1e-6 # overflow防止のための小さな値
def absmax_quantize(self, x):
if self.flg_before_linear:
# パターン①: 通常は[-Qb, Qb]にスケール: 式(4), (5)を適用
gamma = torch.abs(x).max().clamp(min=self.epsilon)
x_scaled = x * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(-self.Qb, self.Qb - 1)
else:
# パターン②: Reluなどの非線形関数前の場合は[0, Qb]にスケール: 式(6)を適用
# 論文中には記載はないですが、スケールが異なるためスケーリングの基準として使っているgammaもetaを反映した値にすべきだと考えます。
eta = x.min()
gamma = torch.abs(x - eta).max().clamp(min=self.epsilon)
x_scaled = (x - eta) * self.Qb / gamma
x_q = torch.round(x_scaled).clamp(0, self.Qb - 1)
# STE
x_q = (x_q - x_scaled).detach() + x_scaled
return x_q, gamma
# 独自のsign関数の定義
# torch.signは0を0として扱ってしまう。custom_signはW>0を+1に、W≦0を-1とする。
def custom_sign(self, x):
return (x > 0).to(torch.int8) * 2 - 1
def quantize_weights(self):
# 式(3): alphaの計算
alpha = self.weight.mean()
# 式(1),(2): 重みの中心化とバイナリ化
weight_centered = self.weight - alpha
weight_binarized = self.custom_sign(weight_centered)
# 式(12): betaの計算
beta = self.weight.abs().mean()
# STE (weight_binarizedとスケールを合わせるためweight_centeredをweight_scaledにスケールしています。)
weight_scaled = weight_centered / (weight_centered.abs().max() + self.epsilon)
weight_binarized = (weight_binarized - weight_scaled).detach() + weight_scaled
return weight_binarized, beta
def forward(self, x):
# 1. LayerNorm (input: x, output: x_norm)
x_norm = self.layernorm(x)
# 2. Absmax Quatization (input: x_norm, output: x_q, gamma)
x_q, gamma = self.absmax_quantize(x_norm)
# 3. 1-bit Weights化 (input: -, output: w_q, beta)
w_q, beta = self.quantize_weights()
# 4. テンソル積(⊗) (input: x_q,w_q, output: x_matmul)
x_matmul = torch.nn.functional.linear(x_q, w_q, self.bias)
# 5. Dequantization (input: x_matmul,beta,gamma, output: output)
output = x_matmul * (beta * gamma / self.Qb)
return outputこれで動くかどうか試しつつ、適宜コード修正していきたいと思います。
(オプション4:論文ではさらに、モデル並列化のためのグループ量子化について記載されています。これは今後必要に応じて実装していきます。)
ここまで作ったものをGithub上に置いています。
2. BitNetの検証
上記で作成したBitNetを事前学習できるか試していきます。
読みやすさの関係で別ページを作成しました。以下をご参照頂けたらと思います。
参照
この記事が気に入ったらサポートをしてみませんか?
