BitNetにおけるSTE(Straight-Through Estimator)の実装

2024年3月30日 16:11

はじめに

現在、私は以下のような試みをしています。

BitNetとは

BitNetとはweightとactivationを量子化する手法の1つで、特にweightを{-1, 0, 1}の3値に量子化するBitNet b158はベースとしているLlama2の性能を上回ることを示し、注目を浴びました。
その実装の中で、量子化（つまりFloat16や32ではなくより離散的な値を扱う様にする処理）を行うとBackward時に微分ができないため学習がうまくできないという問題が発生します。
したがって、これをSTE（straight-through estimator）という技術使って回避する必要があります。

STEとは

STE（straight-through estimator）は割と簡単な発想です。

Forward時はそのまま量子化を行い、
Backward時は量子化の処理だけバイパスしてしまおう

という発想で実装を行うみたいです。（下図）

BitNetにおけるSTEの実装と疑問

このSTEを、BitNetのweightの量子化(-1, 1の2値化)の関数に適用させるとすると以下の様になるはずです。（詳細は記事をご確認ください。）
少しわかりづらいですが、quantize_weightsでは、self.weightの①中心化、②スケーリング、③量子化を行っています。（self.weightの値はfloatの範囲の値ですが、量子化によって[-1, 1]の範囲にされます。なので、②スケーリング、③量子化は同時に行われていると考えることができます。）

def quantize_weights(self):
    # 式(3): alphaの計算
    alpha = self.weight.mean()

    # 式(1),(2): 重みの中心化とバイナリ化
    weight_centered = self.weight - alpha
    weight_binarized = self.custom_sign(weight_centered)

    # 式(12): betaの計算
    beta = self.weight.abs().mean()

    # STE (weight_binarizedとスケールを合わせるためweight_centeredをweight_scaledにスケールしています。)
    weight_scaled = weight_centered / (weight_centered.abs().max().clamp(min=self.epsilon))
    weight_binarized = (weight_binarized - weight_scaled).detach() + weight_scaled

    return weight_binarized, beta

このうち、③量子化のみをバイパスするために以下の様にdetach()を用いています。

weight_binarized = (weight_binarized - weight_scaled).detach() + weight_scaled

detachされた値はbackward時は無視され、forward時にはweight_binarizedが、backward時にはweight_scaledが用いられます。

しかし、他の方のBitNetの実装（例えばBitNet、Bit-Transformers、1bitLLM/bitnet_b1_58-3B）や公式のFAQ見ると軒並み、①中心化、②スケーリング、③量子化の全てバイパスしている実装となっています。

w_quant = w + (weight_quant(w) − w).detach()

本当にこれで良いのか？となったため、いくつかのパターンで実装したBitNet（BitLlama）を学習させてLossを確認してみました。

1. BitLinearの2値化におけるSTE

実験

まずは通常のBitLinearのweightの量子化(-1,1の2値化)において、以下の3つを検証します。

STEによるバイパス: ③量子化のみ
STEによるバイパス: ②スケーリング、③量子化
STEによるバイパス: ①中心化、②スケーリング、③量子化

モデルサイズは127M params、range3/wiki40b-jaを1 epochだけ事前学習させました。以下が結果です。

結果

想像通り、1の③量子化のみをバイパスするパターンが一番安定して、大きくLossを減少させています。
一方、2の②スケーリング+③量子化をバイパスするパターンや、3の①中心化②スケーリング③量子化全てをバイパスするパターンも若干不安定ながらもLoss自体は減少します。（またLossの下がり方自体は2,3でそれほど変わりませんが、若干3の方が曲線が不安定に見えます。）

考察

なぜ、スケーリング(や中心化)をバイパスに含めてもある程度Lossが下がるのでしょうか。これは、直感的には以下のような理解ができます。

STEは、勾配が0となってしまう箇所を近似する（コード的にはバイパスする）技術。
スケーリング+量子化を関数fとする。勾配降下法にてfの微分を行うとき、本来は量子化部分をSTEでバイパスする。
しかし、スケーリング部分を一緒にSTEでバイパスしても、wのスケールが変わるだけで勾配降下法でwが最適値に向かって移動する方向（勾配ベクトル）は変わらない。

つまり、f(w)の微分がf'(w)の時f(aw)の微分はaf'(w)であり、f'(w)もaf'(w)もベクトルの大きさは違うけれど向きは同じだよね。だからスケーリングも一緒にバイパスしてしまっても勾配効果法は機能するよね。ということなんだと思います。
ただし、勾配ベクトルの大きさは変わるので学習率が実質的には変化した状態となるため、以下のことが起こったのだと思います。

学習曲線がいくらか不安定(おそらく発散もしやすい状態であることが予想される)
学習が遅い

また、中心化に関してはBitNetでは採用されていますが、BitNet b158では採用されておらず、ほぼ正負に均一に分布しているのではないかと考えられます。（BitNetの論文には-1, 0, 1の割合はそれぞれ同数程度存在するという感じのことが書いてあった気がします。）
中心化はそもそもそれほど機能していないためバイパスしても問題なかったのではないと考えます。

結論

中心化、スケーリング、量子化の全てをバイパスしてもある程度問題はなさそうですが、より安定した学習を求めて③量子化のみをバイパスする実装を採用したいと思います。

2. BitLinear 1.58bの3値化におけるSTE

実験

BitLinear b158の場合でもBitLinearとほぼ同様の結果が得られると想定されます。BitLinear b158では、少しパターンを変えて実験をしてみています。
BitLinear b158には中心化の処理はないためなくなっています。
具体的なコードを以下の通りです。STE部分以外に関しての詳細は別記事をご確認ください。

def quantize_weights(self):
    # 式(3): betaの計算
    beta = self.weight.abs().mean().clamp(min=self.epsilon)

    # 式(1),(2): 重みの量子化(-1, 0, 1)とクリップ
    # 各値は{-1, 0, +1}の中で最も近い整数に丸められます。
    weight_scaled = self.weight / beta
    weight_trinarized = torch.round(weight_trinarized)
    weight_trinarized = torch.clamp(weight_trinarized, -1, 1)

    # STE　　1
    weight_trinarized = (weight_trinarized - self.weight).detach() + weight

    # STE 2
    # weight_trinarized = (weight_trinarized - weight_scaled).detach() + weight_scaled

    # STE 3
    # weight_scaled = self.weight / self.weight.abs().max().clamp(min=self.epsilon)
    # weight_trinarized = (weight_trinarized - weight_scaled).detach() + weight_scaled

    return weight_trinarized, beta

スケーリング+量子化をバイパスするパターン(STE 1)に加え、スケーリングにおいてBackward時に使うweight_scaleを２パターン試しました。

STE: スケーリング+量子化
STE: 量子化のみ（weight_scaled: self.weight / self.weight.abs().mean()）
STE: 量子化のみ（weight_scaled: self.weight / self.weight.abs().max()）

#2におけるself .weight.abs().mean()とはbetaであり、量子化のみバイパスとしてまず考えられる選択肢だと思います。それに加えて、BitLinearで用いたスケーリングself.weight.abs().max()を#3として採用しています。

モデルサイズは127M paramsで変わりないですが、予算の関係上range3/wiki40b-jaを0.29 epoch(12000 steps)で学習を止めました。

結果

結果は以下の様になりました。

意外にも以下2点が確認できました。

absmeanで量子化後とスケールを合わせて、量子化のみバイパスするパターン(#2 量子化(absmean))では学習が安定せずLossが下がらなくなる。
#1 スケーリング+量子化をバイパス、#3 量子化(absmax)のみバイパスではLossの下がり方にほとんど差が見られなかった。

考察

これに関してはなぜだかよくわかりませんでした。
#2 量子化(absmean)が本来のバイパスとしては自然な気がします。ただ、self.weight / self.weight.abs().mean()ではweight_scaledが[-1, 1]の間に必ずしも収まらないです。{-1, 0, 1}(あるいは{-1, 1})に量子化しバイパスする際にはその前のスケーリングを[-1, 1]範囲に収まるように近似しなければいけないのでしょうか。

しかしそうなるとなぜスケーリング+量子化の両方をバイパスしてもほとんど差が見られないのかに疑問が残ります。
どなたかわかる方がいればご指摘いただければ幸いです。

結論

#1 スケーリング+量子化をバイパス、#3 量子化(absmax)のみバイパスのどちらでもそれほどLossの変化が変わらなかったため、より計算量の少ない#1 スケーリング+量子化をBitLinear 1.58bでは採用しようと思います。

3. BitLinear 1.58bのabsmax量子化におけるSTE

実験

BitNetにはweightの量子化に加え、activationの量子化(absmax quantization)を行います。したがって、activationにおける量子化もSTEによるバイパスが必要になります。以下にコードを示します。詳細は別記事をご確認ください。

def absmax_quantize(self, x):
    # スケールgammaの計算（absmax quantization）
    gamma = torch.abs(x).max().clamp(min=self.epsilon)

    # 重みの量子化とクリップ
    x_scaled = x * self.Qb / gamma
    x_q = torch.round(x_scaled)
    x_q = torch.clamp(x_q, -self.Qb, self.Qb - 1)
    
    # STE 1
    x_q = (x_q - x_scaled).detach() + x_scaled

    # STE 2
    # x_q = (x_q - x).detach() + x
    
    return x_q, gamma

absmax quantizationもスケーリング+量子化を実施するため、以下の２パターンを確認しました。

STE: 量子化のみバイパス
STE: スケーリング+量子化をバイパス

モデルサイズは127M paramsで変わりないですが、予算の関係上range3/wiki40b-jaを0.29 epoch(12000 steps)で学習を止めました。
また、この時のweightのSTEは２章における#1 スケーリング+量子化をバイパスを採用しています。

結果

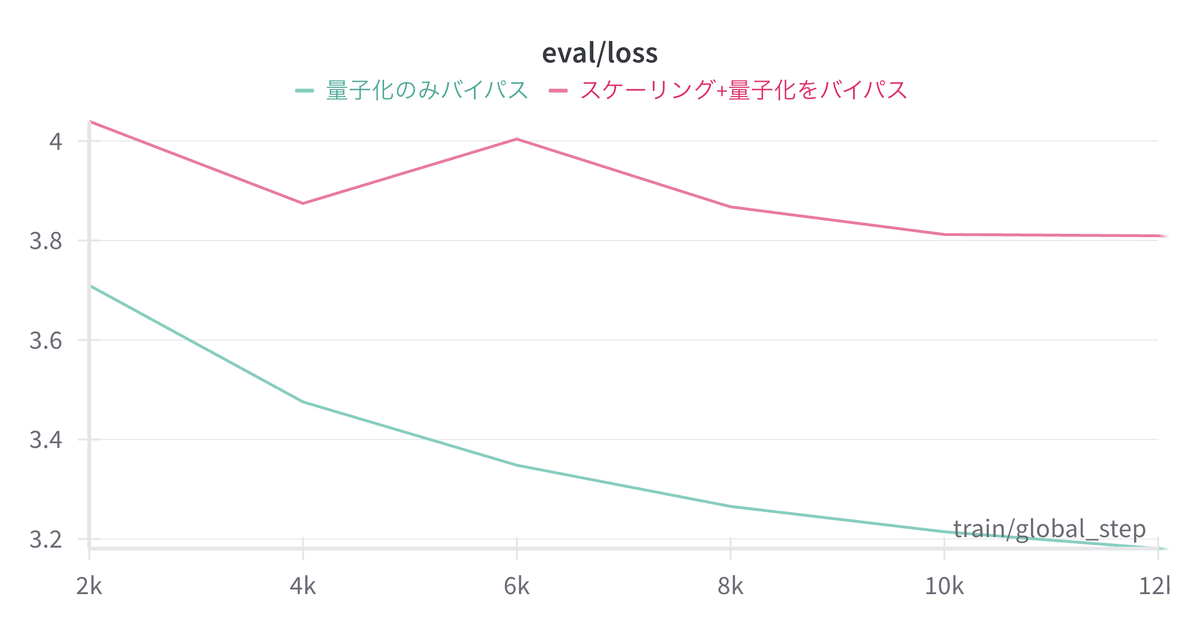
こちらは想像通り、スケーリングをバイパスするとLossの下がり方が不安定かつ下がりづらいことが確認できました。

考察

結果は想像通りです。１章での考察と同様、実質的な学習率のブレから学習が不安定になっているのではと考えられます。そうなるとますます2章の結果が不思議ではあります。

結論

activationの量子化において、#1 量子化のみバイパスを採用します。
activationの量子化の内容はBitLinearとBitLinear 1.58bでほとんど変わらないので、BitLinearにおいても同様に#1 量子化のみバイパスを採用することとします。

その他

参照

この記事が気に入ったらサポートをしてみませんか？