
統計学とは?なんでしょうか?履修を通じて自問自答してみました。(その2「確率」・「推計・検定」)
統計学とは?なんでしょうか?履修を通じて自問自答してみました。
(その2「確率」・「推計・検定」)
1‐2、確率(probability)[確率分布]
続いて確率分布についてです。
さきほど「統計学は確率です」という先生の言葉を記しましたが、
まさにその
「確率」(probability)です。
まず、主な確率分布について。
離散型確率分布には「二項分布」と「ポアソン分布」などがあります。
(離散型というのはサイコロの目や勝ち負けのようにはっきりとした結果が出るもの)
また
連続型確率分布というものが一方にあります。「正規分布」、「z分布(標準正規分布)」、「t分布」、「ⅹ²分布(カイ二乗分布)」、「F分布」などがあります。
(連続型というのは身長や体重のように細かくしていくと連続的なもののことを言います)
まずは、
正規分布(Normal Distribution)についてです
エクセル関数は =NORMDIST(平均、標準偏差、X、関数形式)
と記入していきます!
例えば:授業では「成人男性の身長が170センチ以下になる確率」などを求められます。
=NORMDIST(平均、標準偏差、X、関数形式)
ここのカッコに入れる「関数形式」には2つの形式があります
1、true(1):累積密度 (面積を表すものなので身長とか体重にはピッタリ)
2、false(0):分布の高さ その時点の座標の高さを計ります
(※ 個別の値がはっきりしているのに良い、個数とか売上金額とか?)
つづいて、表か裏か?みたいな結果が2種類しかないベルヌーイ試行(bernoulli trial)をn回繰り返したとき、成功の回数を確率変数とする確率分布が
二項分布(binominal distribution)
と言うそうです。
エクセルでは(=BINOM.DIST)
で簡単に二項分布確率が計算できるそうです。
実際の計算時には(カッコ)の中に数値などを入れていきます。
=BINOMI.DIST(成功数,試行回数,成功率,関数形式)
の数値などを半角英数字で入れます。(※成功率は%なので 5パーセントとかなら「0.05」と入れます、また関数形式のところは二項分布だと「FALSE」あるいは「0」を入れます。)
確率分布を特徴づける定数を「母数(parameter)」と言うそうです。分布を仮定するのは標本ではなく母集団(全体)であるためだからとのこと。推測統計学にも登場します。
二項分布の性質について授業で以下のような説明がありました。
1、実現するのは(0か1)(勝つか負けるか、表か裏かみたいな)
2、n回(X₁、X₂、X₃、・・・・Xn)
(1=確率Pで起こる、0=確率=p-1)(当然ですよね:二つしかないので)
3、平均=(1-p)×0+p×1=p
4、分散 V(x)=(1-p)×(0-p)²+p(1-p)²
=((1-p)×(0²‐0p‐p0+p²))+(p×(1-2p+p²))
=((1-p)×p²)+(p-2p²+p³)
=(p²-p³)+(p-2p²+p³)
=p―p²=p(1-p)となります。
なので分散は p(1-p)
標準偏差はそれの平方根なので p(1-p)の√(ルート)です
ですよね。
(※ ちなみに、この公式の数式の展開に十分以上かかりました。中学3年以来の計算でした。ここをきちんとやらないと自分的には納得できませんでした。実力不足を痛感しています。)
ま、エクセル関数の
=BINOMI.DIST(成功数,試行回数,成功率,関数形式)
は「n」が少ない時には有効であると伺いました。
繰り返しになりますが、
標準正規分布における、任意の標準化変量zの確率密度はエクセルの
(=NORM.S.DIST(z、関数形式)で求められます。
これも同じく数値などをカッコ内に入れていきます。
以下のように
=NORM.S.DIST(平均,標準偏差,X,関数形式)
(※正規分布での関数形式のところは二項分布だと「TRUE」あるいは「1」を入れます)
ちなみに、ポアソン分布はnが大きい時にいいそうです!
エクセル式は(=POISSON.DIST(x、λ、関数形式))
「大数の法則」(たいすうのほうそく)(law of large numbers)についても学びました。
教科書によると
より大きい標本から求めた平均が、真の値(母平均)に近づくことを、言います。とこれは直観的に考えてもそう思いますよね。
授業ではサイコロをN回投げての散らばり具合のお話が出ました。投げた回数のN回が多くなればなるほど散らばりが少ない正規分布の曲線に近づくことを説明していただきました。(Nが増えれば、増えるほど、標準偏差の値は小さくなります。)
また「中心極限定理」(central limit theorem)も同じような意味で学びました。
ウィキペディアからの引用ですが
大数の法則によると、ある母集団から無作為抽出した標本の平均は標本の大きさを大きくすると母平均に近づく。これに対し中心極限定理は標本平均と母平均との誤差を論ずるものである。多くの場合、母集団の分布がどんな分布であっても、その誤差は標本の大きさを大きくしたとき近似的に正規分布に従う。
と書かれています。要するに、標本平均と母平均には、その分布に差がないんやで!ということでしょうか?
また個人的に「期待値」(expectation)という概念のことがわかっていませんでした。
期待値とは確率分布の平均であるとのこと。
試行の結果として期待される値なので「期待値」と呼ぶそうです!
サイコロを1回振って「1」が出る期待値は「6分の1」ですね。2回ふると{6分の1+6分の1=3分の1}ですよね。
「期待値ビジネス」というものがあり、数をたくさん集める事で安定した収益が見込めるビジネスを言うそうです!例えば「保険」などがそれに当たるという説明は直観的に理解出来ました。
この統計の部分に含まれるかわかりませんが、以下
「モンテカルロ・シュミレーション」(モンテカルロ法)についても学びました。
これは個人的にとても面白かったです!乱数を使って計算をするという手法です!乱数で100年後1000年後までをも予測してそれの統計を見ていくというようなものです!
経営の実験(シュミレーション)などに実際に使えるのではというものでした。
乱数はエクセル関数で
RAND(0~1)
RANDBETWEEN(a~b)
などを使って行います。
授業では
売上150億 経費130億 利益20億(売上高利益13.3%)の会社が
赤字になる確率をシュミレーションしてみました。
これは「データ分析ツール」の「乱数発生」で行いました。
「データ」→「データ分析」→「乱数発生」→ここで(正規分布)(均一)などを選択します。その後、データ選択(変数の数、乱数の数)して→結果
これで計算してみると何と、4年に1回の赤字の確率が出て来ました!
その後、では経費を5%削るとどうなるのか?や
固定客を増加させたり・多角化して利益率を上げる戦略はどうか?みたいな、
シュミレーションをしたことが1000年単位で見えて来ます。それを教えていただいた時にこうしたシュミレーションって、なんて面白いんだろうと思いました!そして5%コストカットするよりも多角化して利益率を上げるような戦略の方が有効なのでは?みたいな仮説が見えてくることが分かりました。
2、推計(推測統計学)& 検定
ある事象を観測するのにすべてのデータを取るということはとても難しいです!なので、少ない観測データから全体の特性を推測する必要が出て来ます。
対象全体を「母集団」(population)or(universe)と言います。この「母集団」という言葉、良く出てきます。
実験や観測によって母集団から取り出した1部のデータを標本(sample)と言います。この取り出す作業をサンプリング(抽出)と言います。
<サンプリング>(標本抽出)
サンプル調査は会社員をしていた方なら何度か行ったりデータを見せてもらったりデータを統計処理して情報にしたものを見たりしたのではないでしょうか?
いくつサンプルを取れば最大効果が得られるのか?みたいな問題も実際に出て来ます!
サンプル調査には、コストと時間がかかります。
なので、最大公約数のサンプルの数がわかるとコストを無駄にかけないで済みます。
また何度か調査を繰り返して、その都度、平均を取るなどの方法もあるそうです。
標本統計量には
(標本平均)、S²(標本分散)、S(標本標準偏差)というのがあります。
これらから母数の 母平均:μ、母分散: 、母標準偏差: を推定して行くことが「推計」です。
標準偏差の計算式は以下ですよね(Pは平均)
標準偏差はそれの平方根なので p(1-p)のルート√ です!
です
そして、
標本平均の標準偏差=S(標本標準偏差)=標準偏差/nのルート
となります!
推定のプロセスは
「前提条件」→分布の決定→範囲の決定→「区間推定」と進めていきます。
(※前提条件は=「1、標本に基づく」、「2、標本取らず仮説に基づく」 があるそうです)
標本に基づく推定ですと
「標本X」の確率分布(平均・標準誤差)を求めます。
(エクセルの 分析ツール でも一発ですよね)もちろん、
p(1-p)のルート√
でも求められます。
(※「データ」→「データ分析」→「基本統計量」→データ選択して→結果)
仮説に基づく推定では
仮説を例えば「40%」くらいか?と設定して
何回も100人の平均を取るそうです!
授業では
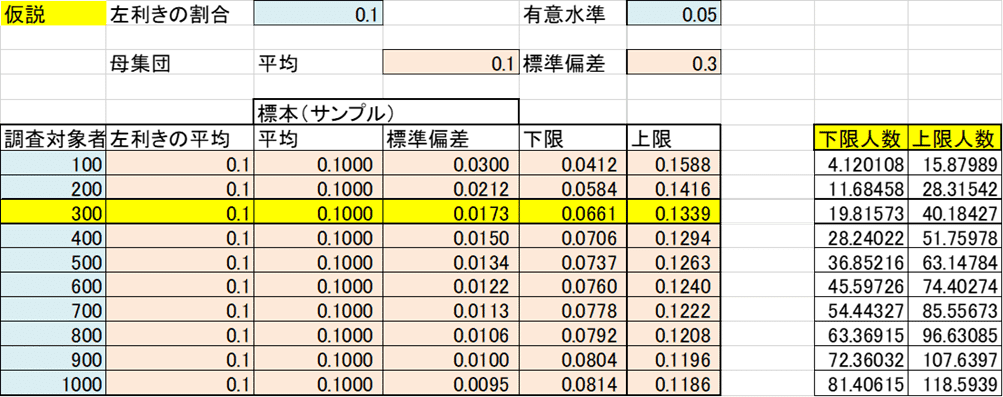
左利きの人数の割合の問題が出ました!
以下のグラフにもあるように
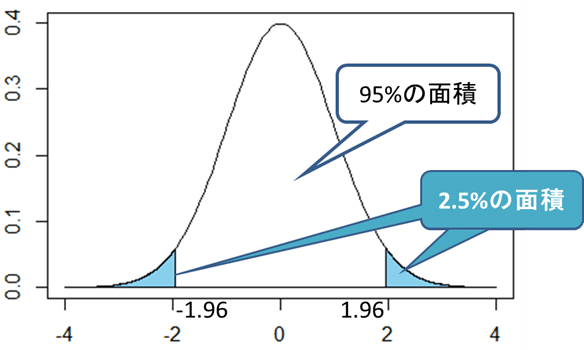
1、有意水準を5%とします(青い部分)
2、(仮説)左利きは10% とします
3、日本人1億人から300人を標本抽出(サンプリング)するとします。
平均は10%の 仮説なので 0.1 ですよね
また標準偏差を300人から求めると以下になります!
母集団の標準偏差=p(1-p)のルート√ =0.3 となります。
とすると、
標本標準偏差=標準偏差/nのルート=0.3/ルート300=0.0173
となります。
ここからエクセル関数の出番です!
=NORMINV(確率=0.025(2.5%)、平均=0.1、標準偏差=0.0173)
=NORMINV(確率=0.975(97.5%)、平均=0.1、標準偏差=0.0173)
を入れてエクセルの計算に任せると
(左利きの割合が)0.066(6.6%)~0.134(13.4%)
人数にすると ×300で 20人~40人(300人中)となるそうです。
こうして仮説を立てると、その仮説下においての計算結果が求められるのがわかります。
以下 仮説の推定結果です!
続く 範囲の推定ですが以下のグラフをご覧ください。
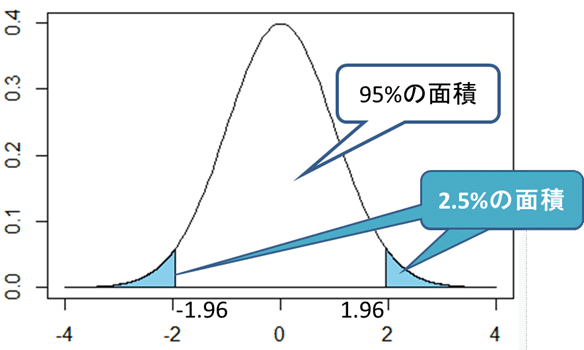
この標準分布の中の面積の確率で確からしさを推定していきます。
真ん中の95%になるものは誤差5%でほぼ確かと言えるのではないか?という前提で考えているということ、だそうです。ここの部分を「信頼区間」と言います。
そして左右の青い部分(左右 足すと5%になります)ここを「有意水準」と言うそうです!
授業では「有意水準」を「珍しさの基準」=「端っこの確率」=「端っこの面積」と言い換えて教えてくれました。(グラフとこの言葉があると、わかりやすいくないですか?)
エクセル関数では =NORMINV と記述するそうです。
具体的には =NORMINV(累積確率, 平均, 標準偏差)と入れます!
(以下は 入れる要素の説明です)(「累積確率」とはその区間の推定確率です!上のグラフの青い部分の左側だと(0.025)=2.5% 右の青い部分は (0.975)=97.5% となります。
累積確率:もとの値(x)を求めるための累積確率を指定します。(※0.975とか0.025とか)
平均:分布の算術平均(相加平均)を指定します。
標準偏差:分布の標準偏差を求めます。
エクセルでは
(=AVERAGE は平均を求める式)
(=VAR.P が標本分散を求める式)
(=STDEV.P が標本標準偏差を求める式)となります。
2‐2、検定
「検定」とはなんでしょうか?
Google辞書ですと以下のように書かれていました。
検定:ランダム標本の観測値から母集団についての仮説の成否を確率的に推断する、統計処理(を行うこと)。
教科書にはこんな風に書かれていました。
仮説検定:仮説が正しいにしては起きにくいことが起きたと考えられる場合、そもそも仮説は間違いであったと判断する。
続いて
検出力:母集団に差があるときに“ある”と正しく判断できる能力。
仮説検定は、論理学みたいな数学のレトリックみたいな話の展開なので、ちょっとややこしいです!
仮説は正しいか?→矛盾がありました。間違っていました。→仮説を棄却(その仮説間違っているやん)→仮説ではないものが正しい!
みたいな、論理の流れなんです。
(もちろん、仮説が正しいこともありますが、いろいろ読んでいると基本的には仮説を棄却して結論を導き出すという方法を取るそうです!)
(背理法というものは同じ考え方ですよね?文系の方は「背理法」と考え方が同じと書くと少し、この考え方がとっつきやすいのではないでしょうか?
背理法の詳細は、以下の「コトバンク」を参照ください。特に以下の部分の記述が面白かったです!引用「背理法は古代ギリシアから知られ、ユークリッドの『幾何学原本』は「素数は無限個存在する」ことを背理法で証明している。」)
参照先:https://kotobank.jp/word/%E8%83%8C%E7%90%86%E6%B3%95-113192
仮説がさきほどの正規分布曲線で
青い部分に入ってしまっていたら「あかん!」(矛盾・誤り)とするということです!
となると仮説の反対側の考えが正しいと推測することが仮説検定です!
A=Bやと仮説を立てたら「矛盾」していた、従ってA≠Bやで!という。
仮説は英語で「Hypothesis」(ハイポセシス)と言います。
仮説の立て方の言い方を変えます。
帰無仮説(Null Hypothesis)というらしいのですが
授業では
この仮説は 通常「変化」「差」「効果」がないという前提の仮説を取り
それが棄却(矛盾や誤りがあるので)されれば
「変化した」「差がある」「効果あり」ということが証明されるというもの。
二項対立構造で、ものすごく極端な考え方ですが、確かにロジックは正しいですよね。
エクセル関数では
=NORM.S.DIST(平均,標準偏差,X,関数形式)
と書きます。Xになる確率は?みたいな。
そのほかにもいくつかの検定方法があります。
t検定、z検定、F検定 などなど
これらの計算は
エクセルの「データ分析」(分析ツール)で検定が出来ます。
「データ」→「データ分析」→「t検定」(他の検定もあります)→データ選択して→結果
次回は「回帰分析」「ベイズの定理」です!
この記事が気に入ったらサポートをしてみませんか?
