富山県 公立高校入試 2019年
こんにちは。
アナ雪2を見ていないので見てみたい、八重です。
早速ですが、今日は昨日に引き続き富山県 公立高校入試 2019年 大問6(3)(4)を解いていきたいと思います。
問題
下の図のように、縦、横ともに1cmの等しい間隔で直線が引かれた方眼紙があり、縦線と横線の交点に、点A,B,C,D,E,F,Q,Rがある。点Pは、Aを出発して、線分AB,BC,CD,DE,EF,FA上を、A→B→C→D→E→F→Aの順にAまで動く。点Pが、Aを出発してからx cm動いたときの三角形PQRの面積をy ㎠とするとき、次の問いに答えなさい。

(1)x = 4のとき、yの値を求めなさい。
(2)点PがCからDまで動くときの、xの変域を求めなさい。
(3)下の図は、xとyの関係を表したグラフの一部である。このグラフを完成させなさい。

(4)三角形PQRの面積が6㎠となるxの値は2つある。その値をそれぞれ求めなさい。
解答
(3)下の図は、xとyの関係を表したグラフの一部である。このグラフを完成させなさい。

(4)三角形PQRの面積が6㎠となるxの値は2つある。その値をそれぞれ求めなさい。
(3)のグラフより、点Pが辺AB上と辺CD上にあるときに面積が6㎠になる。
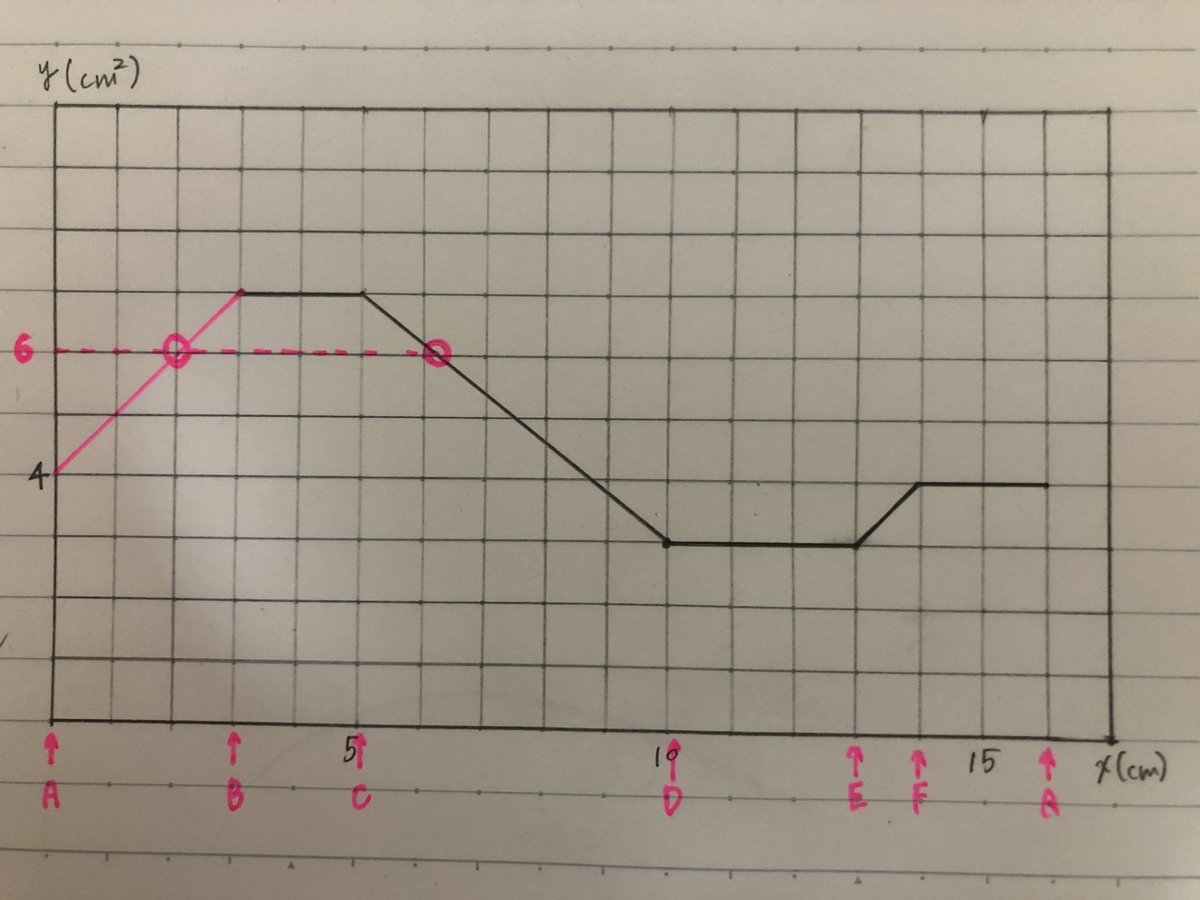
線分QRとの距離が6cmになれば良いので、辺ABにおけるものは x=2cm
同様に、辺CDにおけるものも求める。
x=5+5÷4=6,25cm
従って、答えは x= 2cm 、6,25cm
明日は中学受験の過去問を解きます!
それでは、今日はこの辺で終わりにします。お疲れ様でした。
最後までご覧くださり、有難うございました。
