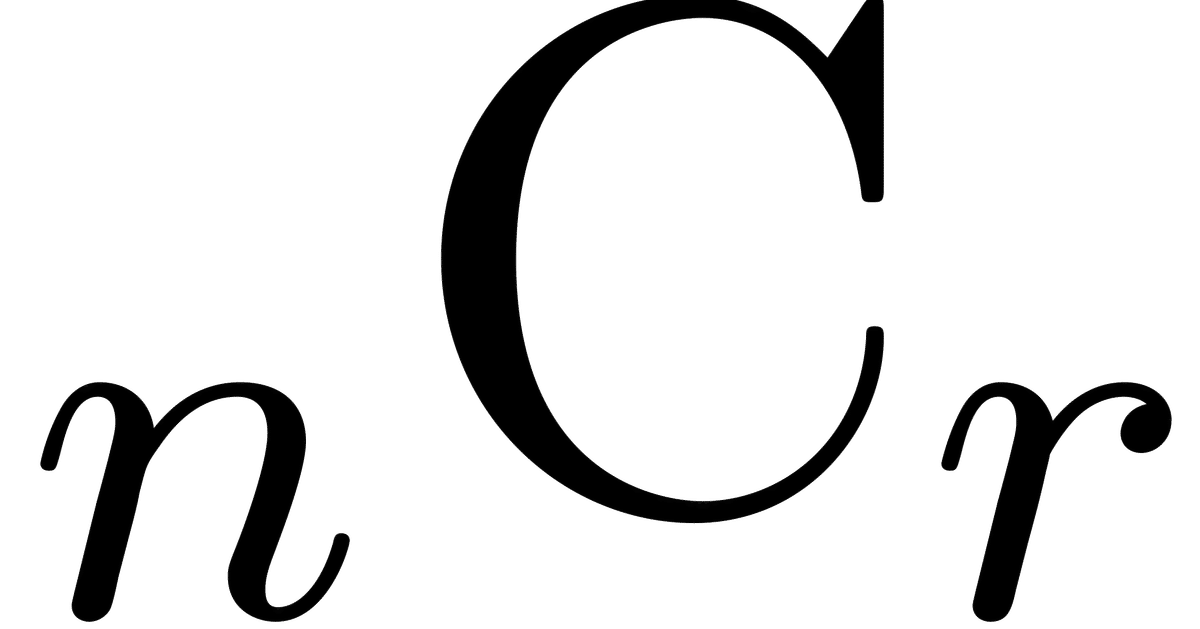
「場合の数」って簡単??
皆さん、こんにちは。量子コンピュータのビジネスを自社で企画できないかと最近密かに思っているぶーさんです。数学の分野の一つである「場合の数」とみんな大好き「将棋」にまつわる面白いエピソードをYouTubeで拝見したので、本日は皆さんにそちらのエピソードを簡単に紹介します。
数学が好きで好きでたまらない数学人間も、数字なんて見たくない数学ダイキライッって人も、みんな読んだくさい。
※なるべく誤った情報は記載しないように配慮していますが、間違い等気になる点があれば容赦なくご指摘ください。
目次
・「場合の数」を懐かしむ
・最近のAI将棋って凄い!
・「場合の数」×「将棋」の未解決問題
・まとめ
■「場合の数」を懐かしむ
皆さん、「場合の数」って覚えていますでしょうか?
そうです。あれです。中学か高校かどちらか忘れましたが、数学の授業で習ったアレです。何て説明したら良いか悩みますが、こんな感じでしょうか。
「ある事象について、その事象が起こる場合の総数」を考える数学の一分野。
何となく伝わったかと思います。折角なので、例題を1問。
Question.
区別できない6個の玉を次のようにわける方法は何通りあるか?
(1)3組に分ける。但し0個の組があってもよい。
(2)3組に分ける。但し0個の組はないものとする。
下の答えを見る前に是非考えてみてください!
.
.
.
.
Answer.
(1)全ての場合を書き出すと次の通り。
(6.0.0),(5.1.0),(4.2.0),(4.1.1),(3.3.0),(3.2.1),(2.2.2)
よって、答えは 7通り
(2)(1)より答えは 3通り
皆さんいかがでしたでしょうか。なんか懐かしいですよね。
場合の数ってどんなイメージがありますか??
場合の数の最初のイメージって、こんなん数えたら誰でも答え分るやん、って感じでなんか簡単そうなイメージでした。実際には、「すべて書き出す」という方法だけでは、試験では時間制限があり解ききれないので、幾つかの公式や型を利用してその時その時の問題に応用することが必要でしたよね。また、問題によっては「抜け漏れなく」かつ「重複なく」正確に数え上げることが難しく苦戦した思い出もあります。時には特定の事象ではなく、「n個の~」とか「n種の~」という様な一般化された場合の数を求められることもあり、一筋縄でいきませんでした。
そう思うと、私が最初に場合の数に抱いたイメージは受験においては甘かった様な気がしますね。
でもでもですね。やっぱり、受験のように時間の制限に縛られていない日常においては、「特定の事象の場合の数を求める」という場合の数の問題は地道に数え上げるだけでいいので、簡単なような気もしてきます。簡単というより、頑張ればどんな問題でも解けそう、って感じです。パソコンの計算能力が爆発的に進化したこの時代においてはなおさら、パソコンに地道に数えさせればどんな問題も解けるような気がします。
皆さんはどう思いますか?
■最近のAI将棋って凄い!
いきなりなのですが、私は将棋が大好きです。
将棋ウォーズというアプリで毎日修行しております。
級位は今のところ4級です。特異な戦法は升田式石田流です。

将棋のルールを簡単に説明しますと、1対1の対決制で、9×9の盤面に各プレイヤーが8種20個の駒を互いに並べ、相手の王(玉)の駒を取ったら勝ちというゲームです。各駒には決められた動きがあり、それに則って駒を動かさないといけません。また、相手から奪った駒を自分のものとして使うことができたり、駒によっては相手陣に入ると成るといって、裏返しにして動きを変えることもできたりします。有名な騎士としては羽生善治九段や加藤一二三氏がいらっしゃいます。最近では藤井聡太7段も非常に有名ですね。
そんな将棋ですが、近年あるものが注目されています。
そう、AIです。一昔前まではプロの棋士がコンピュータに負けるはがないと思われていましたが、人間の頭脳の動きをコンピュータで真似しようとするAIの時代の流れに乗って、今ではプロ棋士をも打ち負かす将棋AIソフトが多数生み出されています。2017年に将棋ソフト「PONANZA」が佐藤天彦名人という当時プロ棋士会でもかなり強い位置にいた棋士に2連勝し、将棋界に衝撃が走りました。2020年の今ではAI将棋ソフトは当時よりさらに強くなっていることでしょう。また、将棋AIソフトは棋力が凄まじいだけでなく、各盤面の形勢を数値で評価したりもしてくれます。
こういったAIソフトはどうやって、プロ棋士をも打ちまかすような棋力を実現させているのでしょうか。起こりうる盤面全てをコンピュータに覚えさせて、それぞれの局面での最適手を覚えさせているのでしょうか?
基本的に、人間がある局面において次の1手を考える際には、ルール上打つことのできる手から、最善の手は何かを探します。人間の計算能力には限界がありますので、実際には全通りの手を検討するのではなく、打ち手の経験や直感から有効だと思われる手に絞って次の打ち手を考えます。一方、AIソフトの様なコンピュータは人間とは違って、とてつもない計算能力を持っていますので、全ての場合を計算して最善手を見つけているような気がします。
実は上の考え方は間違っています。現代の最先端のコンピュータの計算能力を以てしても将棋の全打ち手を計算(して比較)することは不可能なのです。
では、なぜ現代のスーパーコンピュータを以てしても計算しきれないのか?
次の章でこの話をしていきます。
(※将棋のAIソフトは実際にはAIの学習方法の一つである「強化学習」と呼ばれるものを利用して最善手を導き出しています。AIの将棋ソフトが実際にこの強化学習でどのような計算をしているのかという話はここでは深く立ち入りません。私自身詳しくない、というのと本題から外れてしまいますので、ご容赦ください。)

※これは羽生善治九段がまるで敗色濃厚の様な苦渋な表情を浮かべながら何だかんだ勝ってしまう、というユニークな写真です。本記事とは関係ありません。
■「場合の数」×「将棋」の未解決問題
前章で近年の将棋において凄まじい進化を遂げているAIは将棋の各盤面での全打ち手を計算しているわけではない、というより計算できない、という話をしました。では何故計算不可能なのでしょうか。
答えはシンプルで、将棋というゲームでは実現可能な局面、つまり将棋における場合の数があまりにも多すぎる、からです。
つまり、計算する対象の場合の数があまりに多すぎてコンピュータの計算能力の限界を超えているのです。そもそも、将棋において実現し得る局面の場合の数ってどれぐらいあるのでしょうか?
そうなんです。「将棋で実現し得る盤面は何通りあるか?」という場合の数に関する問題は未だに解かれていないのです。以下である論文を紹介しますが、そこでは将棋で実現し得る盤面数(以後、「実現可能局面数」と呼ぶ)は、10の60乗以上10の70乗未満であることが証明されていて、さらに、実現可能局面数はおよそ10の68乗~10の69乗ではないかと推測されています。
※実現可能局面数の定義については以下で紹介する論文での定義に基づきます
何となく気合でどんな問題でも解けそうだと思っていた場合の数にも”超難問”はあるようです。。。この問題が簡単に解けない理由は将棋のその複雑なルールと、場合の数の問題の性質にあります。将棋には、同じ列に「歩」という駒を2つ置いてはいけない二歩というルールや、それ以上駒を動かせなくなるような駒の打ち方をしてはいけないルールがあります。また、場合の数では、「抜け漏れなく」かつ「重複なく」すべての場合を調べる必要があります。
その為、将棋の細かいルールを守りながら、同種の駒を区別せずに、また最初の駒の配置からが実現しないような盤面を含めずに正確に実現可能局面数を数え上げるという途方もない作業が必要になります。
「場合の数」の問題なんて時間さえかければ誰でも解けるやんって考えていた昔の自分をぶん殴ってやりたいですね。
実は将棋だけでなく、囲碁やチェス、オセロ等のボードゲームでも実現可能局面数はまだ数え上げることができていないのです。
オセロなんて黒か白だけで、なんか本気出せば数え上げれそうなのに、それほど甘くないようです。「場合の数」恐るべし!!
私がこの記事を書くきっかけになった以下の動画では将棋の実現可能局面数が10の100乗以下であることを証明しています。私が大好きなYouTuberのヨビノリ氏の動画です。
動画タイトル:場合の数で実現可能局面数を見積もる【将棋と数学】
https://www.youtube.com/watch?v=7QcpShRfqGA&t=225s
10の100乗以下であることの証明はそれほど難しくありません。
次に、将棋の実現可能局面数についてより詳細に分析している論文を紹介します。上の動画での評価からさらに踏み込んだ評価がされています。数え上げの要素から以下の不要要素を取り除いています。
① 同一局面を 2 度以上数えている(同種の駒を区別しているため)
②同じ枡に複数の駒がある
③行きところのない駒がある
④二歩である
⑤双方の玉が隣接している
⑥先手番なのに後手玉に王手がかかっている(=決着ついてる)
⑦先手玉に実現不可能な王手がかかっている
⑧その他の理由で初形から進み得ない配置となっている
上記の分析の結果、将棋の実現可能局面が10の60乗以上10の70乗未満であることが導き出せます。正確な数え上げには⑧の要素を全て排除する必要がありますが、これがこの問題を解くネックになっています。
文系出身の私でもじっくり読めば理解できる内容でしたので、将棋好きの方や面白そうと思った方は是非論文にチャレンジしてみて下さい。ちなみには私は途中で何回か頭がパンクしそうになりました。。。。
『将棋における実現可能局面数について』
(篠田 正人 奈良女子大学理学部)
■まとめ
本記事では、「場合な数」にまつわる未解決問題について紹介してきました。「場合の数」が気合で数え上げればどんな問題も解ける分野ではないことは理解してもらえたかと思います。将棋で実現しうる盤面の場合の数が未だに未知数と聞いて、皆さんはどう思われましたか?
私はこのことを知った時に驚いたの同時になるほどな、とも感じました。ある事象について、「抜け漏れなく」かつ「重複なく」場合の数を求めるのはそりゃ難しいよな、と。
場合の数に限った話ではありませんが、物事を「抜け漏れなく」かつ「重複なく」考えるのは大事ですよね。ロジカルシンキングの概念の一つに「MECE(ミーシー)」と言う考え方があります。これは「Mutually Exclusive and Collectively Exhaustive」の略で、「互いに重複しておらず、全体として漏れがない」という意味です。まさしく「場合の数」の問題で求められる考え方です。
皆さんも是非、この「MECE」を鍛えるべく将棋の実現可能局面数について考えてみてはいかがですか??
余談ですが、私が生きている間にこの将棋の実現可能局面数の問題が解かれるとすれば、そこで量子コンピュータが活躍するのでは、とこっそり思ています。
ではでは。本日はここまで。
