
空気抵抗のある落下運動
物体に重力$${mg}$$が働くときの落下速度は
$${m\dfrac{dv}{dt}=mg}$$(Newton's 2nd law)
$${v=\displaystyle\int gdt=gt+C}$$
初期条件$${(t,v)=(0,v_o)}$$より
$${v_0=g×0+C}$$ $${C=v_o}$$ よって $${v=gt+v_0}$$であり
時間$${t}$$の経過と共に鉛直下向きの速度は1次関数的に無限に増えていく。
しかし実際には空気抵抗があり、例えば空から落ちてきた雨粒によって傘に穴が開くことはない。あくまで真空中での話である。
では、空気抵抗がある場合はどうなるのか。
一般に空気抵抗は物体の速度の1次に比例するときと2次に比例するときがあるが、どういう条件でそれぞれの場合になるかは後で考えることにして、速度の1次と2次それぞれについて調べたことを書く。
1 抵抗が速度に比例する落下運動
運動方程式は
$${m\dfrac{dv}{dt}=mg-kv=-k\Big(v-\dfrac{mg}{k}\Big)}$$
変数分離して $${\dfrac{dv}{ v-\dfrac{mg}{k} }=-\dfrac{k}{m}}$$
積分して $${\ln\Big({v-\dfrac{mg}{k}}\Big)=-\dfrac{k}{m}t+C}$$
$${v-\dfrac{mg}{k}=\exp\Big({-\dfrac{k}{m}t+C}\Big)}$$
$${v=\dfrac{mg}{k}+\exp\Big({-\dfrac{k}{m}t+C}\Big)=\dfrac{mg}{k}+C'\exp\Big({-\dfrac{k}{m}t}\Big)}$$
初期条件$${(t,v)=(0,v_0)}$$より
$${v_0=\dfrac{mg}{k}+C'\exp\Big({-\dfrac{k}{m}×0}\Big)=\dfrac{mg}{k}+C', C'=v_0-\dfrac{mg}{k}}$$
よって
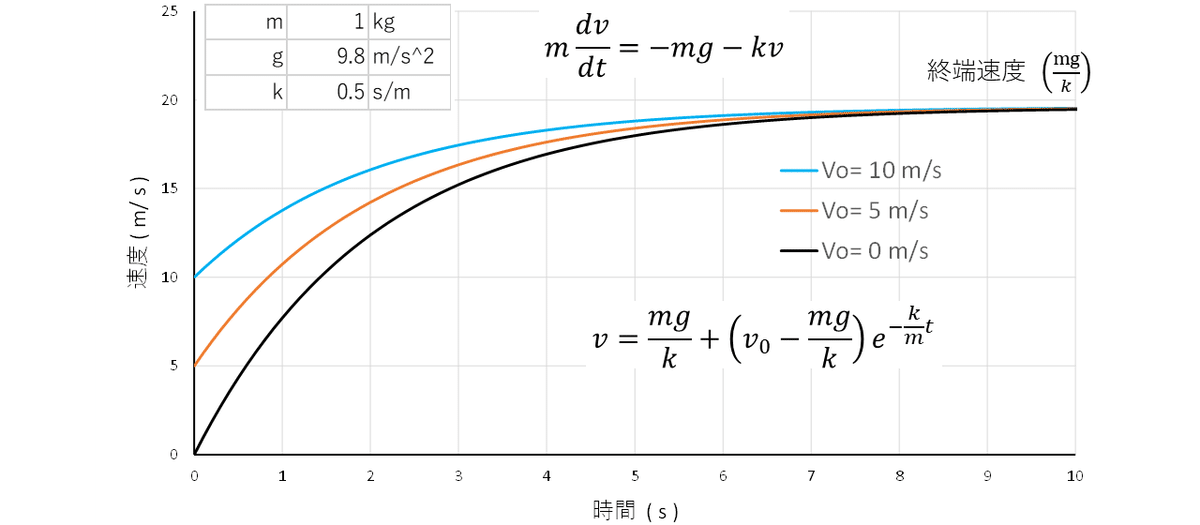
$${v=\dfrac{mg}{k}+\Big(v_0-\dfrac{mg}{k}\Big)\exp\Big({-\dfrac{k}{m}t}\Big)}$$ である。
$${t\rightarrow \infty}$$のとき
$${v\rightarrow \dfrac{mg}{k}+\Big(v_0-\dfrac{mg}{k}\Big)×0=\dfrac{mg}{k}}$$
やがて、物体は$${v_\infty=\dfrac{mg}{k}}$$(終端速度)に達すると等速で落下する。
2 抵抗が速度の2乗に比例する落下運動
運動方程式
$${m\dfrac{dv}{dt}=mg-kv^2}$$ $${\dfrac{dv}{dt}=g-\dfrac{k}{m}v^2=g\Big(1-\dfrac{k}{mg}v^2\Big)}$$
変数分離して
$${\dfrac{dv}{1-\dfrac{k}{mg}v^2}=gdt}$$ $${\dfrac{dv}{\Big(1+\sqrt{\frac{k}{mg}}v\Big)\Big(1-\sqrt{\frac{k}{mg}}v\Big)}=gdt}$$
$${\dfrac{1}{2}\Bigg(\dfrac{1}{1+\sqrt{\frac{k}{mg}}v}+\dfrac{1}{1-\sqrt{\frac{k}{mg}}v}\Bigg)dv=gdt}$$
積分して
$${\dfrac{1}{2\sqrt{\dfrac{k}{mg}}}\Bigg(\ln\Big\lvert1+\sqrt{\frac{k}{mg}}v\Big\lvert+\ln\Big\lvert1-\sqrt{\frac{k}{mg}}v\Big\lvert\Bigg)=gt+C}$$
$${\ln\Bigg\lvert\dfrac{1+\sqrt{\frac{k}{mg}}v}{1-\sqrt{\frac{k}{mg}}v}\Bigg\lvert=2\sqrt{\dfrac{k}{mg}}(gt+C)}$$
$${\Bigg\lvert\dfrac{1+\sqrt{\frac{k}{mg}}v}{1-\sqrt{\frac{k}{mg}}v}\Bigg\lvert=\exp\Big\{{2\sqrt{\dfrac{k}{mg}}(gt+C)}\Big\}}$$
$${=e^{2C}\exp\Big({2\sqrt{\dfrac{k}{mg}} gt}\Big)=C'\exp\Big({2\sqrt{\dfrac{kg}{m}} gt}\Big)}$$
← $${1-\sqrt{\dfrac{k}{mg}}v>0}$$ 即ち$${v<\sqrt{\dfrac{mg}{k}}}$$のとき $${\lvert \lvert}$$の中は正
$${1-\sqrt{\dfrac{k}{mg}}v<0}$$ 即ち$${\sqrt{\dfrac{mg}{k}}< v}$$のとき $${\lvert \lvert}$$の中は負
$${1+\sqrt{\dfrac{k}{mg}}v=\pm\Big(1-\sqrt{\dfrac{k}{mg}}v\Big)C'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)}$$
$${=\pm C'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)\mp\sqrt{\dfrac{k}{mg}}vC'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)}$$
$${\sqrt{\dfrac{k}{mg}}v\pm\sqrt{\dfrac{k}{mg}} vC'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)=\pm C'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)-1}$$
$${\sqrt{\dfrac{k}{mg}}\Big\{1\pm C'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)\Big\}v=\pm C'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)-1}$$
$${v=\dfrac{\pm C'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)-1}{\sqrt{\dfrac{k}{mg}}\Big\{1\pm C'\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)\Big\}}}$$
初期条件$${(t,v)=(0,v_0)}$$より
$${v_0=\dfrac{\pm C'-1}{\sqrt{\dfrac{k}{mg}} (1\pm C')}}$$
$${\sqrt{\dfrac{k}{mg}} (1\pm C')v_0=\pm C'-1}$$ $${\sqrt{\dfrac{k}{mg}} v_0\pm \sqrt{\dfrac{k}{mg}}C'v_0=\pm C'-1}$$
$${1+\sqrt{\dfrac{k}{mg}} v_0=\pm C'\mp \sqrt{\dfrac{k}{mg}}C'v_0=\pm\Big(1-\sqrt{\dfrac{k}{mg}} v_0\Big)C'}$$
$${C'=\pm\dfrac{ 1+\sqrt{\frac{k}{mg}} v_0}{ 1-\sqrt{\frac{k}{mg}} v_0}}$$
$${v=\dfrac{\pm \Bigg(\pm\dfrac{ 1+\sqrt{\frac{k}{mg}} v_0}{ 1-\sqrt{\frac{k}{mg}} v_0}\Bigg)\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)-1}{\sqrt{\dfrac{k}{mg}}\Bigg\{1\pm \Bigg(\pm\dfrac{ 1+\sqrt{\frac{k}{mg}} v_0}{ 1-\sqrt{\frac{k}{mg}} v_0}\Bigg)\exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)\Bigg\}}}$$
$${=\sqrt{\dfrac{mg}{k}} \dfrac{ \dfrac{ 1+\sqrt{\frac{k}{mg}} v_0}{ 1-\sqrt{\frac{k}{mg}} v_0} \exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)-1}{ 1+\dfrac{ 1+\sqrt{\frac{k}{mg}} v_0}{ 1-\sqrt{\frac{k}{mg}} v_0} \exp\Big({2\sqrt{\dfrac{kg}{m}} t}\Big)}}$$
← 分母分子に$${\Big(1-\sqrt{\frac{k}{mg}} v_0\Big)\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}$$を掛ける
$${=\sqrt{\dfrac{mg}{k}} \dfrac{\Big(1+\sqrt{\frac{k}{mg}} v_0\Big)\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)}{\Big(1-\sqrt{\frac{k}{mg}} v_0\Big)\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}}$$
$${\dfrac{-\Big(1-\sqrt{\frac{k}{mg}} v_0\Big)\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}{+\Big(1+\sqrt{\frac{k}{mg}} v_0\Big)\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)}}$$
$${=\sqrt{\dfrac{mg}{k}} \dfrac{\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\sqrt{\frac{k}{mg}} v_0\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)}{\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)-\sqrt{\frac{k}{mg}} v_0\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}}$$
$${\dfrac{-\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)+\sqrt{\frac{k}{mg}} v_0\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}{+\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\sqrt{\frac{k}{mg}} v_0\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)}}$$
$${=\sqrt{\dfrac{mg}{k}} \dfrac{ \exp\Big({\sqrt{\frac{kg}{m}} t}\Big)-\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}{ \exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}}$$
$${\dfrac{+\sqrt{\frac{k}{mg}} v_0\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\sqrt{\frac{k}{mg}} v_0\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}{+\sqrt{\frac{k}{mg}} v_0\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)-\sqrt{\frac{k}{mg}} v_0\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}}$$
$${=\sqrt{\dfrac{mg}{k}} \dfrac{ \exp\Big({\sqrt{\frac{kg}{m}} t}\Big)-\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}{ \exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}}$$
$${\dfrac{+\sqrt{\frac{k}{mg}} v_0\Big\{\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)\Big\}}{+\sqrt{\frac{k}{mg}} v_0\Big\{\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)-\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)\Big\}}}$$
← 分母分子を$${\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)}$$で割る
$${=\sqrt{\dfrac{mg}{k}} \dfrac{ \dfrac{\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)-\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}{\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}+\sqrt{\dfrac{k}{mg}} v_0 }{1+\sqrt{\dfrac{k}{mg}} v_0\dfrac{\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)-\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}{\exp\Big({\sqrt{\frac{kg}{m}} t}\Big)+\exp\Big({-\sqrt{\frac{kg}{m}} t}\Big)}}}$$
← $${\dfrac{e^{x}-e^{-x}}{e^{x}+e^{-x}}=\tanh x}$$
$${=\sqrt{\dfrac{mg}{k}} \dfrac{\tanh\Big({\sqrt{\frac{kg}{m}} t}\Big)+\sqrt{\frac{k}{mg}} v_0 }{1+\sqrt{\frac{k}{mg}} v_0\tanh\Big(\sqrt{\frac{kg}{m}} t\Big)}}$$ ←分母分子に$${\sqrt{\dfrac{mg}{k}}}$$を掛ける
よって
$${v=\sqrt{\dfrac{mg}{k}} \dfrac{ \sqrt{\dfrac{mg}{k}}\tanh\Big({\sqrt{\dfrac{kg}{m}} t}\Big)+ v_0 }{\sqrt{\dfrac{mg}{k}}+v_0\tanh\Big(\sqrt{\dfrac{kg}{m}} t\Big)}}$$ である。
$${t\rightarrow\infty}$$のとき
$${v\rightarrow\sqrt{\dfrac{mg}{k}} \dfrac{ \sqrt{\dfrac{mg}{k}}×1+ v_0 }{\sqrt{\dfrac{mg}{k}}+v_0×1}=\sqrt{\dfrac{mg}{k}}}$$
この場合の終端速度は$${v_{\infty}=\sqrt{\dfrac{mg}{k}}}$$である。

※ 終端速度の別の求め方
$${m\dfrac{dv}{dt}=mg-kv}$$ 速度一定なので左辺=0 よって $${v_{\infty}=\dfrac{mg}{k}}$$
$${m\dfrac{dv}{dt}=mg-kv^2}$$ 速度一定なので左辺=0 よって $${v_{\infty}=\sqrt{\dfrac{mg}{k}}}$$
(こっちのほうが遥かに簡単やw)
3 空気抵抗
1と2の結果を比べる。
空気抵抗が速度に比例 終端速度
$${v=\dfrac{mg}{k}+\Big(v_0-\dfrac{mg}{k}\Big)\exp\Big({-\dfrac{k}{m}t}\Big)}$$ $${v_\infty=\dfrac{mg}{k}}$$
空気抵抗が速度の2次に比例
$${v=\sqrt{\dfrac{mg}{k}} \dfrac{ \sqrt{\dfrac{mg}{k}}\tanh\Big({\sqrt{\dfrac{kg}{m}} t}\Big)+ v_0 }{\sqrt{\dfrac{mg}{k}}+v_0\tanh\Big(\sqrt{\dfrac{kg}{m}} t\Big)}}$$ $${v_{\infty}=\sqrt{\dfrac{mg}{k}}}$$

ネットで調べたところ、流体中を運動する物体に働く抵抗には粘性抵抗と慣性抵抗があり、物体に対してどちらの抵抗が働くかはレイノルズ数により決まる。
3-1 粘性抵抗(viscous resistance)
流体の分子の物体への衝突に起因し、物体の速度に比例する。具体的には、物体の運動方向前面と後面の衝突回数の差による。(Stokes の抵抗法則)
物体が球形の場合は
$${F_v=6\pi\eta rv}$$ (1)
$${r}$$:物体の半径 $${v}$$:物体の速度
$${\eta}$$:空気の粘性係数($${=1.82\times10^{-5}\text{Ns/m}^2}$$)
である。
3-2 慣性抵抗(inertia resistance)
物体の前面にある流体を押したときの物体の慣性による反作用に起因し,物体の速度の2乗に比例する。(Newtonの抵抗法則)
$${F_i=\dfrac{1}{2}C_d \rho_aSv^2}$$ (2)
$${S}$$:物体の断面積
$${Cd}$$:抗力係数(物体の形状に依存)球体の場合$${=0.5}$$
$${\rho_a}$$:空気の密度($${=1.20\text{kg/m}^3 at 20℃、101.3kPa 65%}$$)
3-3 レイノルズ数(Reynolds number)
$${R_e=\dfrac{慣性抵抗}{粘性抵抗}}$$ である。 ← (1)(2)、$${S=\pi r^2}$$を代入
$${=\dfrac{F_i}{F_v}=\dfrac{\dfrac{1}{2}C_d \rho_aSv^2}{6\pi\eta rv}}$$$${=\dfrac{\dfrac{1}{2}C_d \rho_a\pi r^2 v^2}{6\pi\eta rv}=\dfrac{C_d\rho_a}{12\eta} rv}$$ (3)
すなわち
$${R_e>1}$$のとき 粘性抵抗が優勢
$${R_e<1}$$のとき 慣性抵抗が優勢 である。
また物体の半径、速度が大きいほど慣性抵抗が優勢となる。
ここで雨滴の落下運動を考える。
空気の粘性率$${\eta =18.2\times10^{-6}\text{kg/ms}}$$、密度$${\rho =1.205 \text{kg/m}^3}$$、雨滴は体積$${0.05\text{cm}^3}$$の球体とする。($${0.05\text{cm}^3}$$としたのは、かつて学生実験で滴定をしたときの経験からである)
雨滴の体積$${=0.05\text{cm}^3=5\times10^{-2}\times(10^{-2}\text{m})^3=5\times10^{-8}\text{m}^3}$$
球の体積$${=\dfrac{4\pi}{3}a^3=5\times10^{-8}\text{m}}$$
$${a=\sqrt[3]{\dfrac{3}{4\pi}\times5\times10^{-8}\text{m}^3}=\sqrt[3]{1.193662\times10^{-8}\text{m}^3}}$$
$${=\sqrt[3]{11.93662\times10^{-9}\text{m}^3}=2.285\times10^{-3}\text{m}}$$
空気抵抗が速度に比例する(粘性抵抗優位)条件は
$${R_e=\dfrac{C_d\rho_a}{12\eta} rv <1}$$
$${v <\dfrac{12\eta}{C_d\rho_a r}=\dfrac{12\times 1.82\times 10^{-5} \text{Ns/m}^2}{0.5\times 1.20\text{kg/m}^3\times 2.285\times10^{-3}\text{m}}}$$
$${=15.9\times10^{-2} \dfrac{\text{kg}\times\text{m/s}^2\times \text{s/m}^2}{\text{kg/m}^3\times\text{m}}=0.159\text{m/s}}$$
粘性抵抗のとき($${m\dfrac{dv}{dt}=-mg-kv}$$)
$${k_v=6\pi\eta r}$$
$${=6\times3.14\times1.82\times 10^{-5} \text{Ns/m}^2\times2.285\times10^{-3}\text{m}}$$
$${=78.4\times10^{-8}\text{kg}\times\text{m/s}^2\times\text{s/m}^2\times\text{m}=7.84\times 10^{-7}\text{kg/s}}$$
この速度に達するまでの時間を求めると(初速度$${v_0=0}$$とする)
$${v=\dfrac{mg}{k_v}+\Big(v_0-\dfrac{mg}{k}\Big)\exp\Big(-\dfrac{k}{m} t\Big)}$$より
$${v=\dfrac{mg}{k_v}+\Big(-\dfrac{mg}{k_v}\Big)\exp\Big(-\dfrac{k_v}{m} t\Big)=\dfrac{mg}{k_v}\Big\{1-\exp\Big(-\dfrac{k_v}{m}\Big)\Big\}}$$
$${\dfrac{k_vv}{mg}=1-\exp\Big(-\dfrac{k_v}{m} t\Big)}$$ $${\exp\Big(-\dfrac{k_v}{m} t\Big)=1-\dfrac{k_vv}{mg}}$$
$${-\dfrac{k_v}{m} t=\ln\Big(1-\dfrac{k_vv}{mg}\Big)}$$
$${t=-\dfrac{m}{k_v}\ln\Big(1-\dfrac{k_vv}{mg}\Big)}$$
$${=-\dfrac{0.05\times10^{-3}\text{kg}}{7.84\times 10^{-7}\text{kg/s}}\ln\Big(1-\dfrac{7.84\times 10^{-7}\text{kg/s}\times 0.159\text{m/s}}{0.05\times10^{-3}\text{kg}\times9.8\times\text{m/s}^2}\Big)}$$
$${=-0.00638\times10^{4}\text{s}\times\ln(1-2.54\times10^{-4})}$$
$${=-0.00638\times10^{4}\text{s}\times(-0.000254)=0.0372\text{s}}$$
慣性抵抗のとき($${m\dfrac{dv}{dt}=-mg-kv^2}$$)
$${k_i=\dfrac{1}{2}C_d\rho_aS=\dfrac{1}{2}C_d\rho_a\pi r^2}$$
$${=\dfrac{1}{2}\times 0.5\times 1.20\text{kg/m}^3\times 3.14\times (2.285\times10^{-3}\text{m})^2}$$
$${=4.92\times10^{-6}\text{kg/m}}$$
終端速度
$${v_\infty=\sqrt{\dfrac{mg}{k}}=\sqrt{\dfrac{0.05\times10^{-3}\text{kg}\times9.8\text{m/s}^2}{4.92\times10^{-6}\text{kg/m}}}=9.98\text{m/s}}$$
以上より、落下直後の一瞬(0.0372秒)だけ空気抵抗は速度に比例し(粘性抵抗優位)、すぐに速度の2乗に比例する運動(慣性抵抗優位)になることがわかる。終端速度$${v_\infty}$$は$${9.98\text{m/s}}$$である。
付け足し
$${R_e}$$が1または1付近のときはどうなるのか。
このときは粘性抵抗も慣性抵抗も同程度に働いている。
よって $${m\dfrac{dv}{dt}=mg-k_vv^2-k_iv^2}$$を解くことになるが、速度が変化して$${R_e}$$が0.1以下か10以上くらいの値になれば一方が優勢になる。
