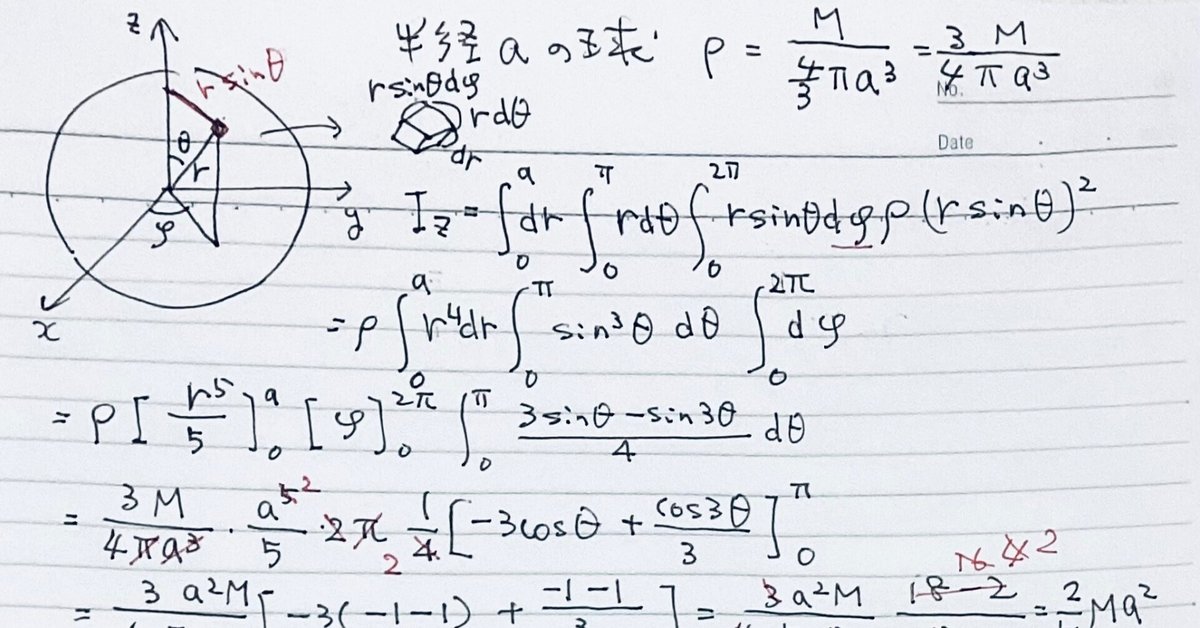
いろいろな慣性モーメントの算出
いろいろな形の慣性モーメント$${I_x、I_y、I_z}$$の算出を書き出してみた。
基本は$${z}$$軸回転として、
直交座標($${x、y、z}$$)では
$${I=\int r^2dm }$$
$${=\int r^2ρdV}$$ ←$${dm=ρdV}$$
$${=\int\int\int ρr^2dxdydz}$$ ←$${dV=dxdydz}$$
$${=\int\int\int ρ(x^2+y^2)dxdydz}$$ ←$${r^2=x^2+y^2}$$
円柱座標($${r、θ、z}$$)では
$${I=\int r^2dm }$$
$${=\int r^2ρdV}$$ ←$${dm=ρdV}$$
$${=\int\int\int r^2ρdr rdθdz}$$ ←$${dV=dr rdθdz}$$
$${=\int\int\int ρr^3drdθdz}$$
極座標($${r、θ、φ}$$)では
$${I=\int (r\sin{θ})^2dm }$$
$${=\int (r\sin{θ})^2ρdV}$$ ←$${dm=ρdV}$$
$${=\int\int\int (r\sin{θ})^2ρdr rdθ r\sin{θ}dθ}$$ ←$${dV=dr rdθ r\sin{θ}dθ}$$
$${=\int\int\int ρr^4\sin^3{θ}drdθdφ}$$
である。
細長い棒

長方形のうすい板

直交軸の定理($${I_z=I_x+I_y}$$)が使えるが、使わなくてもそれほど手間がかかるわけではない。(ただし、うすいものという条件付き)
立方体

細い円環

ちなみに$${\sin^2{θ}=\dfrac{1-\cos2θ}{2}}$$
$${\cos2θ=\cos(θ+θ)=\cos^2θ-\sin^2θ=1-2\sin^2θ}$$
これはすぐに思いついた。
うすい円板

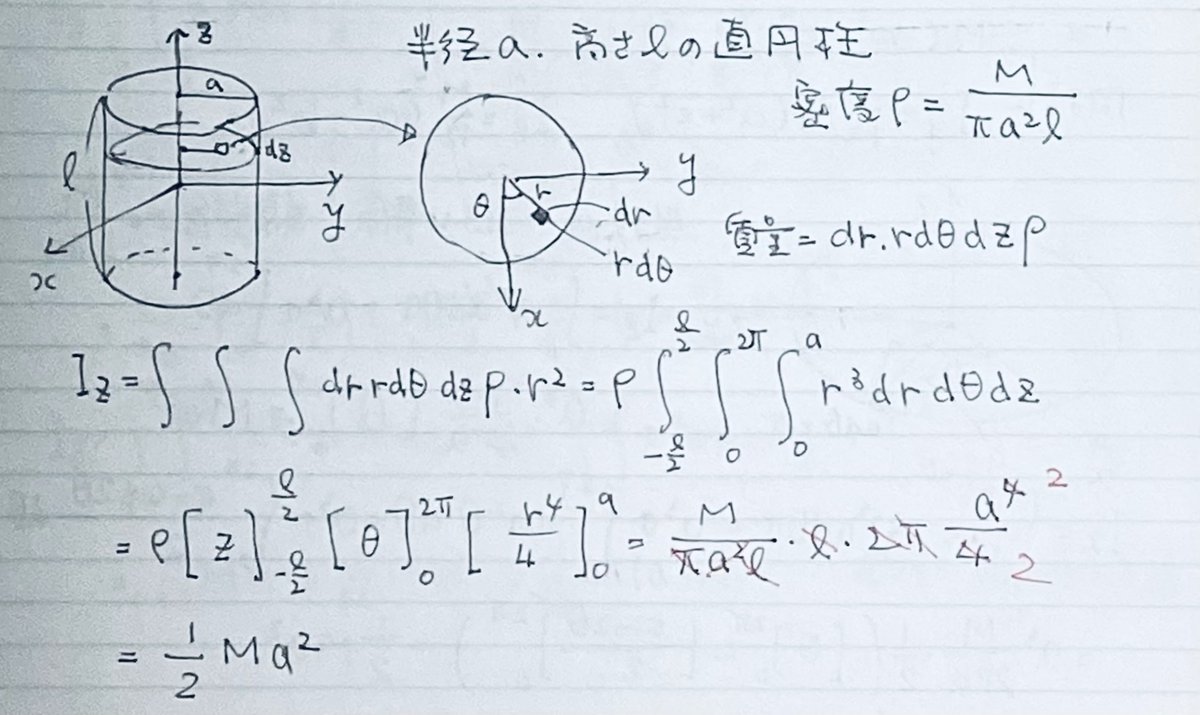
円柱
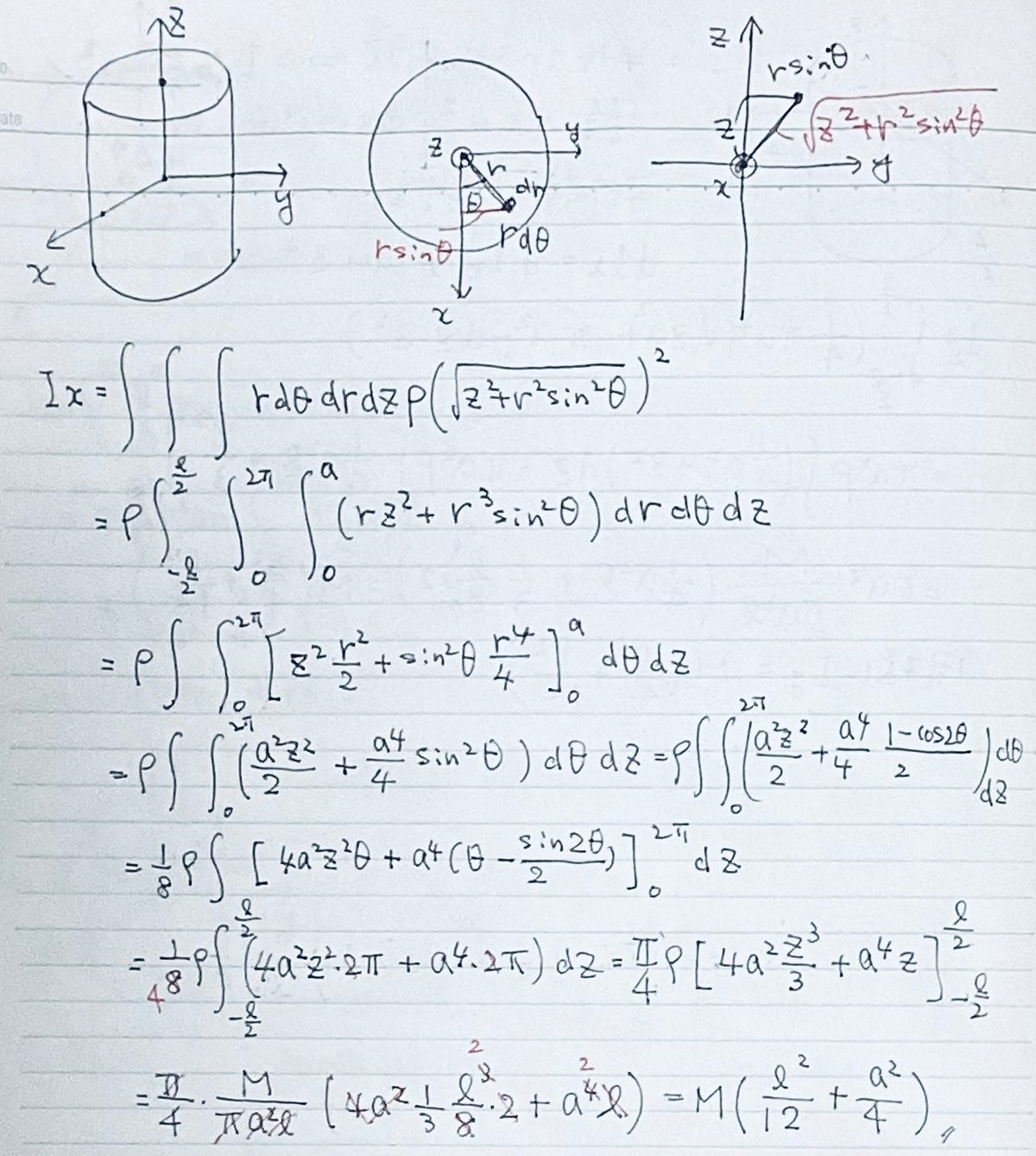
$${I_z}$$はそれほど難しくなく求めることができるが、$${I_x}$$、$${I_y}$$は手続きがややこしい。
先に求めたうすい円板の値を使って、平行軸の定理を使う手もある。
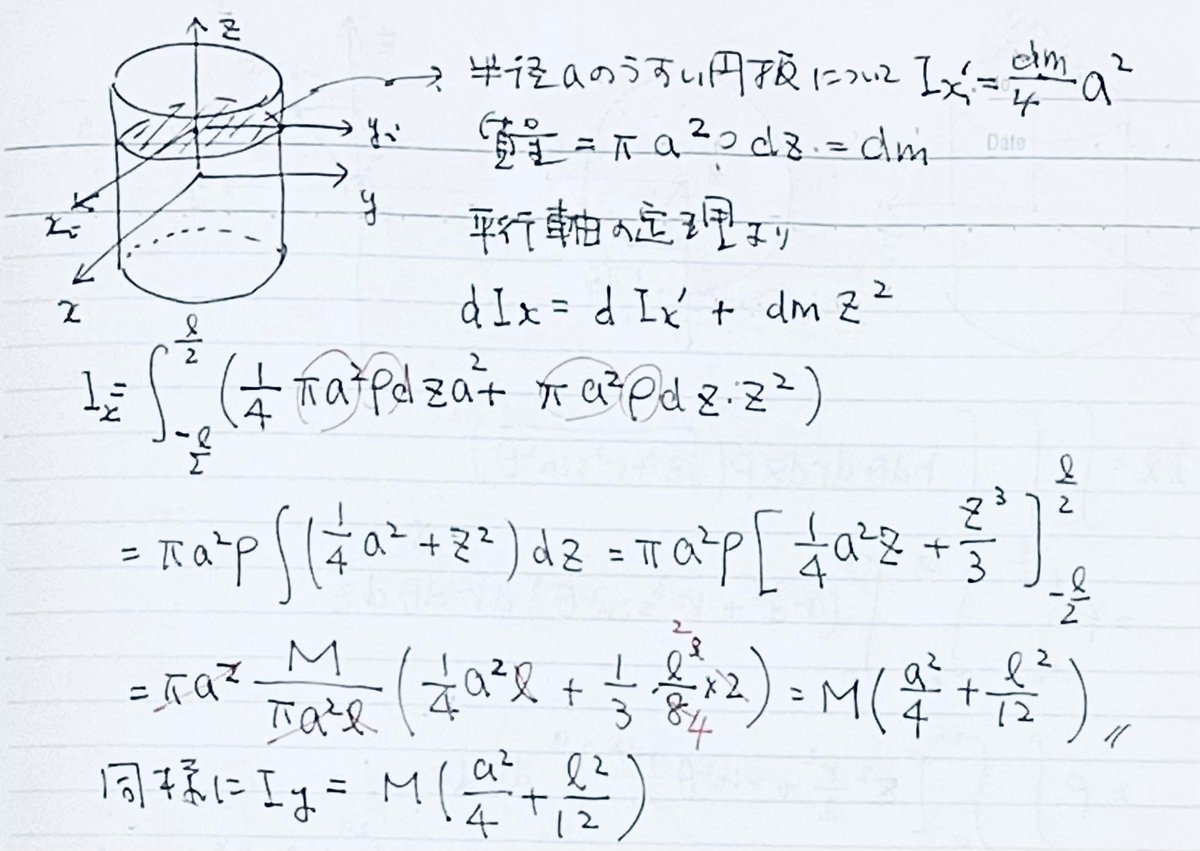
球殻

ちなみに$${\sin^3{θ}=\dfrac{3\sinθ-\sin3θ}{4}}$$
$${\sin3θ=\sin(θ+2θ)=\sinθ \cos2θ+\sin2θ \cosθ}$$
$${=\sinθ(\cos^2θ-\sin^2θ)+2\sinθ \cosθ \cosθ}$$
$${=\sinθ(1-2\sin^2θ)+2\sinθ(1-\sin^2θ)}$$
$${=\sinθ-2\sin^3θ+2\sinθ-2\sin^3θ}$$
$${=3\sinθ-4\sin^3θ}$$
こっちは手間取った。やれやれ。
球
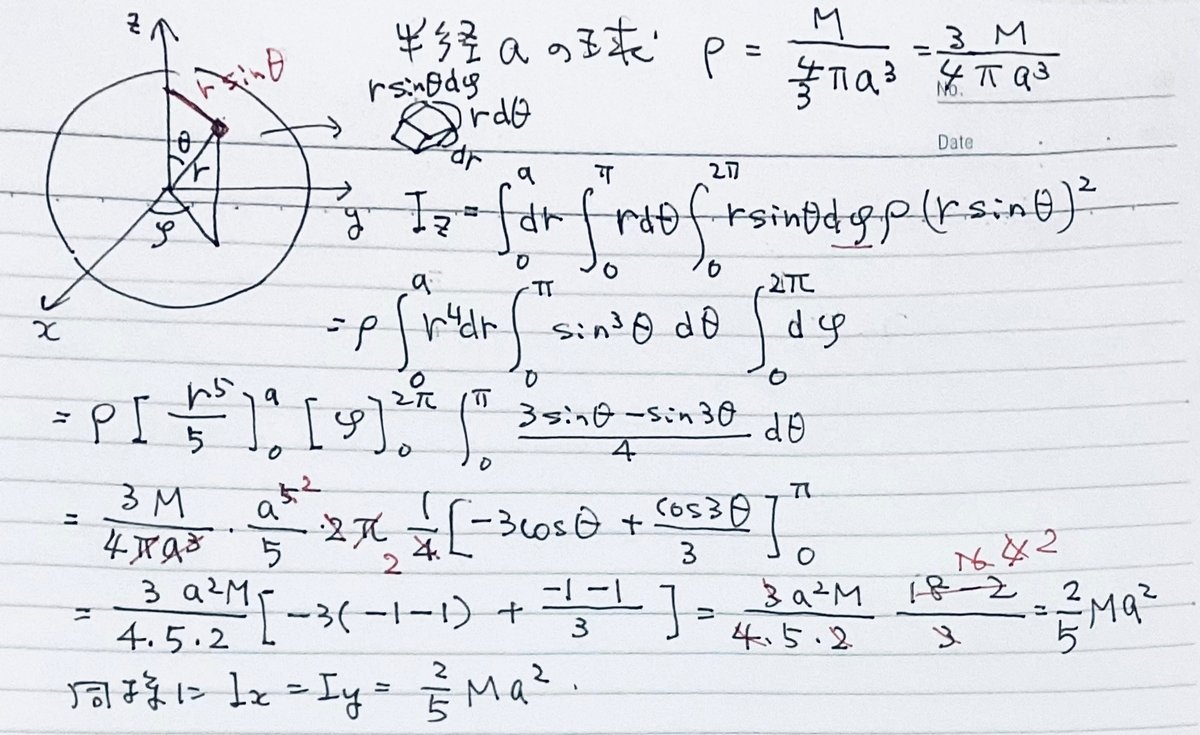
終わりに
手持ちの本やネットで調べ、式の変形を学習しながら書き出した。いろいろなやり方があって奥が深い。
極座標や円筒座標、積分の技を思い出すことができた。よい復習になった。
