極座標､球座標の速度､加速度

すぐに忘れるのでここに書いておく。
いつも忘れた頃に必要になる。困ったものだ。

１ 極座標

　$${\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}r\cos{\theta}\\r\sin{\theta}\end{bmatrix}}$$  $${\begin{bmatrix}v_r\\v_\theta\end{bmatrix}=\begin{bmatrix}\dot{r}\\r\dot{\theta}\end{bmatrix}}$$　　　$${\begin{bmatrix}a_r\\a_\theta\end{bmatrix}=\begin{bmatrix}\ddot{r}-r\dot{\theta}^2\\2\dot{r}\dot{\theta}+r\ddot{\theta}\end{bmatrix}}$$

以下導出
1-0 直交座標上の回転

1-1 速度$${(v_r,v_\theta)}$$

　$${r}$$軸方向の速度$${v_r=\dot{r}}$$、$${\theta}$$軸方向の速度$${v_\theta}$$は$${\dot{\theta}に}$$に$${r}$$を掛けたもの。
　どちらも直感的に理解できる。

1-2 加速度$${(a_r,a_\theta)}$$

　Lagrange’s eq からの$${(a_r,a_\theta)}$$の導出

２ 球座標

　$${\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}r\sin\theta\cos\phi\\r\sin\theta\sin\phi\\r\cos\theta\end{bmatrix}}$$　　　  $${\begin{bmatrix}v_r\\v_\theta\\v_\phi\end{bmatrix}=\begin{bmatrix}\dot{r}\\r\dot{\theta}\\r\dot{\phi}sin\theta\end{bmatrix}}$$

　$${\begin{bmatrix}a_r\\a_\theta\\a_\phi\end{bmatrix}=\begin{bmatrix}\ddot{r}-r\dot{\theta}^2-r\dot{\phi}^2\sin^2\theta\\2\dot{r}\dot{\theta}+r\ddot{\theta}-r\dot{\phi}^2\sin{\theta}\cos{\theta}\\2\dot{r}\dot{\phi}sin\theta+r\ddot{\phi}\sin\theta+2r\dot{\theta}\dot{\phi}\cos\theta\end{bmatrix}}$$

2−0 位置と座標の変換

球座標$${(r,\theta,\phi)}$$から$${z}$$軸で$${\phi}$$､$${\phi}$$軸で$${\theta}$$回転すると直交座標$${(x,y,z)}$$になる。

以上をまとめると

この関係は当然速度、加速度、力でも成り立つ。
　$${\begin{bmatrix}v_x\\v_y\\v_z\end{bmatrix}=A\begin{bmatrix}v_r\\v_{\theta}\\v_{\phi}\end{bmatrix}}$$、　$${\begin{bmatrix}a_x\\a_y\\a_z\end{bmatrix}=A\begin{bmatrix}a_r\\a_{\theta}\\a_{\phi}\end{bmatrix}}$$、　$${\begin{bmatrix}F_x\\F_y\\F_z\end{bmatrix}=A\begin{bmatrix}F_r\\F_{\theta}\\F_{\phi}\end{bmatrix}}$$

2-1 速度$${(v_r,v_\theta,v_\phi)}$$

2-2 加速度$${(a_r,a_\theta,a_\phi)}$$

極座標の時のように
　$${\begin{bmatrix}a_x\\a_y\\a_z\end{bmatrix}=\begin{bmatrix}\ddot{x}\\\ddot{y}\\\ddot{z}\end{bmatrix}=   …  =A\begin{bmatrix}  …  \\  …  \\  …  \end{bmatrix}}$$を導き

　$${\begin{bmatrix}a_x\\a_y\\a_z\end{bmatrix}=A\begin{bmatrix}a_r\\a_\theta\\a_\phi\end{bmatrix}}$$と右辺のAの右側の行列を比較して求めればよい。

しかし､この方法は延々と計算が必要であり、チャレンジしたが力尽きた。
Lagrange's eq で導くことにする。
はじめに一般化力$${Q_r,Q_{\theta},Q_{\phi}}$$と$${F_r,F_{\theta},F_{\phi}}$$の関係を求めておく。
また$${Q_r=-\dfrac{\partial U}{\partial r},   Q_\theta=-\dfrac{\partial U}{\partial \theta},   Q_\phi=-\dfrac{\partial U}{\partial \phi}}$$
　　$${F_r=ma_r,   F_\theta=ma_\theta,   F_\phi=ma_\phi}$$　　である。

Lagrangian を求め､Lagrange's eq に代入する。

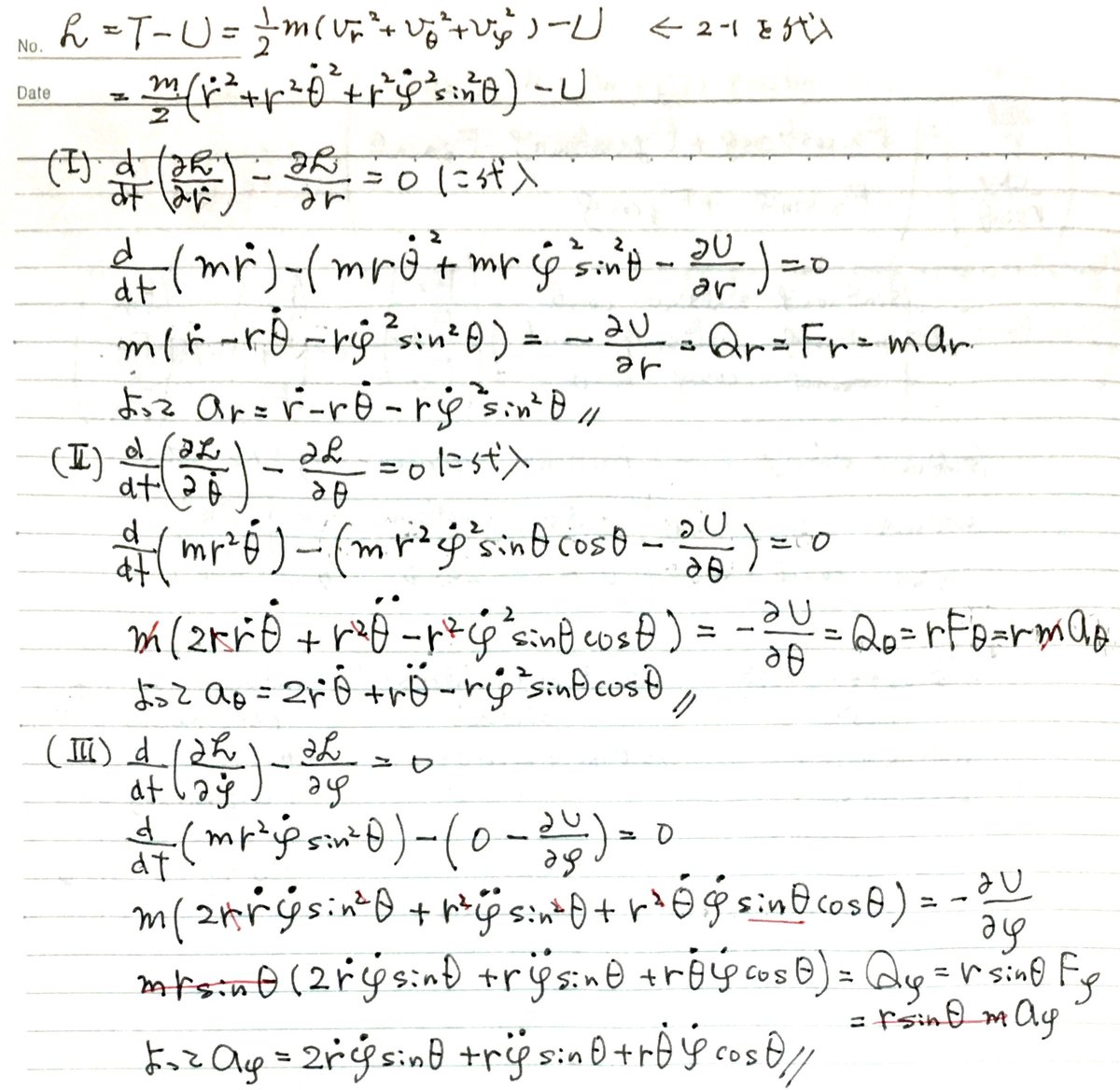
以上である。こういうとき Lagrange's eq は便利である。

　　　　　　　　　　　　　　　　　　　→ 力学､物理数学の目次へ