
Eulerの運動方程式 − 固定軸のない剛体の運動 –
回転運動と並進運動では、固定軸のまわりの剛体の運動について述べた。これで剛体の運動の章を終わる本もあるが、最後に固定軸のない運動が残されている。
1 固定点のまわりの運動(静止座標系)
剛体内にある固定点Oを原点とする静止座標系Oxyzを取り、原点Oのまわりの剛体の運動を考える。
原点Oのまわりの剛体の運動は、瞬間瞬間の原点Oを通る軸のまわりの回転として表現できる。この回転軸の角速度ベクトル$${\bm{ω}}$$は時間の関数である。
$${\bm{ω}=\bm{ω}(t)=\begin{bmatrix}ω_x(t)\\ω_y(t)\\ω_z(t)\end{bmatrix}}$$
当然、角運動量ベクトル$${\bm{L}}$$も時間の関数である。
$${\bm{L}=\bm{L}(t)=\begin{bmatrix}L_x(t)\\L_y(t)\\L_z(t)\end{bmatrix}}$$
$${=\displaystyle\sum_{k=1}^n\bm{r}_k×\bm{p}_k=\displaystyle\sum_{k=1}^n\bm{r}_k×\bm{m}_k\bm{\dot{r}}_k=\displaystyle\sum_{k=1}^n m_k(\bm{r}_k×\bm{\dot{r}}_k)}$$
$${=\displaystyle\sum_{k=1}^n m_k(\bm{r}_k×\bm{v}_k)}$$ ← $${\bm{v}_k=\bm{ω}×\bm{r}_k}$$ なので
$${=\displaystyle\sum_{k=1}^n m_k\{\bm{r}_k×({\bm{ω}}×\bm{r}_k)\}}$$ ベクトル三重積
← $${\bm{a}×(\bm{b}×\bm{c})=(\bm{a}・\bm{c})・\bm{c}-(\bm{a}・\bm{b})・\bm{c}}$$
$${=\displaystyle\sum_{k=1}^n m_k{(\bm{r}_k・\bm{r}_k)・\bm{ω}-(\bm{r}_k・\bm{ω})・\bm{r}_k}}$$
$${=\displaystyle\sum_{k=1}^n m_k{(x_k,y_k,z_k)・(x_k,y_k,z_k)・\bm{ω}-(x_k,y_k,z_k)・(ω_x,ω_y,ω_z)・\bm{r}_k}}$$
$${=\displaystyle\sum_{k=1}^n m_k{(x_k^2+y_k^2+z_k^2)\begin{bmatrix}ω_x\\ω_y\\ω_z\end{bmatrix}-(x_kω_x+y_kω_y+z_kω_z)\begin{bmatrix}x_k\\y_k\\z_k\end{bmatrix}}}$$
$${=\displaystyle\sum_{k=1}^n m_k{\begin{bmatrix}(x_k^2+y_k^2+z_k^2)ω_x-(x_kω_x+y_kω_y+z_kω_z)x_k\\(x_k^2+y_k^2+z_k^2)ω_y-(x_kω_x+y_kω_y+z_kω_z)y_k\\(x_k^2+y_k^2+z_k^2)ω_z-(x_kω_x+y_kω_y+z_kω_z)z_k \end{bmatrix}}}$$
$${=\displaystyle\sum_{k=1}^n m_k{\begin{bmatrix}ω_x(y_k^2+z_k^2)-ω_y x_k y_k - ω_z z_k x_k\\-ω_x x_k y_k + ω_y(z_k^2+x_k^2) - ω_z y_k z_k\\-ω_x z_k x_k - ω_y y_k z_k + ω_z(x_k^2+y_k^2) \end{bmatrix}}}$$
$${={\begin{bmatrix}ω_x\displaystyle\sum_{k=1}^n m_k(y_k^2+z_k^2)-ω_y\displaystyle\sum_{k=1}^n m_k x_k y_k - ω_z\displaystyle\sum_{k=1}^n m_k z_k x_k\\-ω_x\displaystyle\sum_{k=1}^n m_kx_k y_k + ω_y\displaystyle\sum_{k=1}^n m_k(z_k^2+x_k^2) - ω_z\displaystyle\sum_{k=1}^n m_k y_k z_k\\-ω_x\displaystyle\sum_{k=1}^n m_k z_k x_k - ω_y\displaystyle\sum_{k=1}^n m_k y_k z_k + ω_z\displaystyle\sum_{k=1}^n m_k(x_k^2+y_k^2) \end{bmatrix}}}$$
← $${I_x=\displaystyle\sum_{k=1}^n m_k(y_k^2+z_k^2)}$$、$${I_y=\displaystyle\sum_{k=1}^n m_k(z_k^2+x_k^2)}$$
$${I_z=\displaystyle\sum_{k=1}^n m_k(x_k^2+y_k^2)}$$
$${I_{xy}=\displaystyle\sum_{k=1}^n m_kx_k y_k}$$、$${I_{yz}=\displaystyle\sum_{k=1}^n m_k y_k z_k}$$
$${I_{zx}=\displaystyle\sum_{k=1}^n m_k z_k x_k}$$(慣性乗積) とおく
$${={\begin{bmatrix}I_xω_x-I_{xy}ω_y - I_{zx}ω_z\\-I_{xy}ω_x+ I_yω_y -I_{yz} ω_z\\-I_{zx}ω_x- I_{yz}ω_y+ I_zω_z \end{bmatrix}}=\begin{bmatrix}\:\:\:I_x \:\:\:-I_{xy}\:\: -I_{zx}\\-I_{xy}\:\:+ I_y\:\:-I_{yz}\\-I_{zx}\:\:- I_{yz}\:\:+ I_z\end{bmatrix}\begin{bmatrix}ω_x\\ω_y\\ω_z\end{bmatrix}}$$
→ $${\bm{I}=\begin{bmatrix}\:\:\:I_x \:\:\:-I_{xy}\:\: -I_{zx}\\-I_{xy}\:\:+ I_y\:\:-I_{yz}\\-I_{zx}\:\:- I_{yz}\:\:+ I_z\end{bmatrix}}$$(慣性テンソル)
よって $${\bm{L}=\bm{I}\bm{ω}}$$ (1)
この慣性テンソル$${\bm{I}}$$は時間と共に変化するが、それは静止した座標系O-xyzから一点だけ留めたふらふらする剛体を見ているからである。また非対角成分(慣性乗積)が0でないことが事態を複雑にしている。
これを避けるには、慣性テンソルが時間変化せず、かつ慣性乗積がすべて0となるような座標系を取ればよい。しかし、そんな都合のよい座標系が存在するのか。。
存在する。それは剛体と共に動く座標系である。そしてその座標系での慣性テンソルの慣性乗積は0になるのだ。
具体的には慣性テンソルの対角化を行う。しかも対称行列の3つの固有ベクトルはうまいことに互いに直交するのだ。それらを新しい軸とした座標系を取ればよい。
2 対称行列の対角化
以下に対称行列から対角行列を作る手順を示す。
対称行列$${I}$$に対してその固有値を$${λ}$$、固有ベクトルを$${\bm{x}}$$とおくと
$${\bm{Ix}=λ\bm{x}}$$ である。
両辺に$${\bm{E}}$$をかけて $${\bm{EIx}=λ\bm{Ex}}$$、$${\bm{Ix}=λ\bm{Ex}}$$、$${(\bm{I}-λ\bm{E})\bm{x}=\bm{0}}$$
自明な$${\bm{x}=\bm{0}}$$以外の解として$${ |\bm{I}-λ\bm{E}|=\bm{0}}$$を解くと3つの固有値$${λ}$$が得られる。
$${λ=λ_1,λ_2,λ_3}$$
この$${λ}$$を元の式$${\bm{Ix}=λ\bm{Ex}}$$に代入し、それぞれに対応する固有ベクトル$${\bm{x}_1,\bm{x}_2,\bm{x}_3}$$を求める。
$${\bm{x}_1=\begin{bmatrix}u_{11}\\u_{21}\\u_{31}\end{bmatrix}}$$、$${\bm{x}_2=\begin{bmatrix}u_{12}\\u_{22}\\u_{32}\end{bmatrix}}$$、 $${\bm{x}_1=\begin{bmatrix}u_{13}\\u_{23}\\u_{34}\end{bmatrix}}$$
これらは互いに直交するベクトルであり、単位ベクトルとすることができる。
$${\bm{x}_1・\bm{x}_2=\bm{x}_2・\bm{x}_3=\bm{x}_3・\bm{x}_1=0、||\bm{x}_1||=||\bm{x}_2||=||\bm{x}_3||=1}$$
以上より
$${\bm{Ix}_1=λ_1\bm{x}_1}$$、$${\bm{Ix}_2=λ_2\bm{x}_2}$$、$${\bm{Ix}_3=λ_3\bm{x}_3}$$とおける。
これを1つの式で表すと
$${\bm{I}\begin{bmatrix}\bm{x}_1\:\bm{x}_2\:\bm{x}_3\end{bmatrix}=\begin{bmatrix}λ_1\bm{x}_1\:λ_2\bm{x}_2\:λ_3\bm{x}_3\end{bmatrix}=\begin{bmatrix}\bm{x}_1\:\bm{x}_2\:\bm{x}_3\end{bmatrix}\begin{bmatrix}λ_1 0 0\\0 λ_2 0\\0 0 λ_3\end{bmatrix}}$$
ここで$${\begin{bmatrix}\bm{x}_1\:\bm{x}_2\:\bm{x}_3\end{bmatrix}=\bm{U}}$$(直交行列である)とおいて上の式に代入すると
$${\bm{IU}=\bm{U}\begin{bmatrix}λ_1 0 0\\0 λ_2 0\\0 0 λ_3\end{bmatrix}}$$
両辺に$${\bm{U}}$$の逆行列$${\bm{U}^{-1}}$$を左からかけると
$${\bm{U}^{-1}\bm{IU}=\bm{U}^{-1}\bm{U}\begin{bmatrix}λ_1 0 0\\0 λ_2 0\\0 0 λ_3\end{bmatrix}=\begin{bmatrix}λ_1 0 0\\0 λ_2 0\\0 0 λ_3\end{bmatrix}}$$となり、右辺は対角行列となる。
以上まとめると、$${\bm{I}}$$を対角化するには$${\bm{I}}$$の両側を直交行列$${\bm{U}}$$とその逆行列$${\bm{U}^{-1}}$$で挟んで$${\bm{U}^{-1}\bm{IU}}$$を作ればよい。
$${\bm{I}}$$(対称行列)$${\xrightarrow{対角化}}$$ $${\bm{U}^{-1}\bm{I}\bm{U}=\bm{I'}}$$(対角行列)
3 慣性テンソルの対角化
では、1で導いた$${\bm{L}=\bm{I}\bm{ω}}$$(1)の慣性テンソル$${\bm{I}}$$を対角化しよう。
$${\bm{I}}$$の両側を$${\bm{U}^{-1}}$$と$${\bm{U}}$$で挟むには、$${\bm{I}}$$の右側に$${\bm{U}\bm{U}^{-1}}$$を挿入し、両辺に左から$${\bm{U}^{-1}}$$をかければよい。
$${\bm{U}^{-1}\bm{L}=\underline{\bm{U}^{-1}\bm{I}\bm{U}}\bm{U}^{-1}\bm{ω}}$$
この式に $${\bm{U}^{-1}\bm{L}=\bm{L'}}$$(2)、$${\bm{U}^{-1}\bm{ω}=\bm{ω'}}$$(3)、$${\bm{U}^{-1}\bm{I}\bm{U}=\bm{I'}}$$(4)、を代入すると、
$${\bm{L'}=\bm{I'}\bm{ω'}}$$(5)
これが時間に不変な対角化した慣性テンソルを持つ新しい式である。
$${\bm{ω'}}$$について
$${\bm{U}^{-1}\bm{ω}=\bm{ω'}}$$(3) の両辺に左から$${\bm{U}}$$をかけると$${\bm{U}\bm{U}^{-1}\bm{ω}=\bm{U}\bm{ω'}}$$
つまり $${\bm{ω}=\bm{U}\bm{ω'}}$$(6)
これに$${\bm{U}=\begin{bmatrix}\bm{x}_1\:\bm{x}_2\:\bm{x}_3\end{bmatrix}=\begin{bmatrix}u_{11} u_{12} u_{13}\\u_{21} u_{22} u_{23}\\u_{31} u_{32} u_{33} \end{bmatrix}}$$、$${\bm{ω'}=\begin{bmatrix}ω'_x\\ω'_y\\ω'_z\end{bmatrix}}$$を代入すると
$${\bm{ω}=\begin{bmatrix}\bm{x}_1\:\bm{x}_2\:\bm{x}_3\end{bmatrix}=\begin{bmatrix}u_{11} u_{12} u_{13}\\u_{21} u_{22} u_{23}\\u_{31} u_{32} u_{33} \end{bmatrix}\begin{bmatrix}ω'_x\\ω'_y\\ω'_z\end{bmatrix}=\begin{bmatrix}u_{11}ω'_x+u_{12}ω'_y+u_{13}ω'_z\\u_{21}ω'_x+u_{22}ω'_y+u_{23}ω'_z\\u_{31}ω'_x+u_{32}ω'_y+u_{33}ω'_z \end{bmatrix}}$$
$${=ω'_x\begin{bmatrix}u_{11}\\u_{21}\\u_{31}\end{bmatrix}+ω'_y\begin{bmatrix}u_{12}\\u_{22}\\u_{32}\end{bmatrix}+ω'_z\begin{bmatrix}u_{13}\\u_{23}\\u_{33}\end{bmatrix}}$$
すなわち
$${\bm{ω}=ω'_x\bm{x}_1+ω'_y\bm{x}_2+ω'_z\bm{x}_3}$$
軸$${\bm{x}_1}$$、$${\bm{x}_2}$$、$${\bm{x}_3}$$は互いに直交する。
※静止座標系O-xyzでは $${\bm{ω}=\begin{bmatrix}ω_x,ω_y,ω_z\end{bmatrix}}$$
剛体に固定した座標系O-$${\bm{x}_1\bm{x}_2\bm{x}_3}$$では $${\bm{ω'}=\begin{bmatrix}ω'_x,ω'_y,ω'_z\end{bmatrix}}$$ である。
$${\bm{L'}}$$について
$${\bm{U}^{-1}\bm{L}=\bm{L'}}$$(2)の両辺に左から$${\bm{U}}$$をかけて整理すると
$${\bm{L}=\bm{U}\bm{L'}}$$
$${\bm{ω}=\bm{U}\bm{ω'}}$$(6)とあわせて、$${\bm{L}=\bm{Iω}}$$(1)に代入すると
$${\bm{U}\bm{L'}=\bm{I}\bm{U}\bm{ω'}}$$
左から$${\bm{U}^{-1}}$$をかけて
$${\bm{U}^{-1}\bm{U}\bm{L'}=\underline{\bm{U}^{-1}\bm{I}\bm{U}}\bm{ω'}}$$ $${\bm{U}^{-1}\bm{I}\bm{U}=\begin{bmatrix}I'_x\:0\:\:0\\\:0\:\:I'_y\:0\\\:0\:\:0\:\:I'_z\end{bmatrix}}$$とおくと
$${\bm{L'}=\bm{I'}\bm{ω'}}$$ または $${\begin{bmatrix}L'_x\\L'_y\\L'_z\end{bmatrix}=\begin{bmatrix}I'_x\:0\:\:0\\\:0\:\:I'_y\:0\\\:0\:\:0\:\:I'_z\end{bmatrix} \begin{bmatrix}ω'_x\\ω'_y\\ω'_z\end{bmatrix}=\begin{bmatrix}I'_xω'_x\\I'_xω'_y\\I'_xω'_z\end{bmatrix}}$$
$${I'_x,I'_y,I'_z}$$を主慣性モーメント、座標軸$${\bm{x}_1,\bm{x}_2,\bm{x}_3}$$を慣性主軸という。
4 Eulerの運動方程式(慣性主軸系)
では、$${\dfrac{d\bm{L}}{dt}}$$を慣性主軸系O-$${\bm{x}_1\bm{x}_2\bm{x}_3}$$で表そう。
$${\bm{L}}$$自体は静止座標系0-xyzで見ようが、慣性主軸系O-$${\bm{x}_1\bm{x}_2\bm{x}_3}$$で見ようが値は変わらない。
$${\bm{L}=L_x\bm{i}+L_y\bm{j}+L_z\bm{k}=L'_x\bm{i'}+L'_y\bm{j'}+L'_z\bm{k'} (=\bm{L'})}$$
(静止座標系の3軸の単位ベクトル$${\bm{i},\bm{j},\bm{k}}$$は時間変化しないが、慣性主軸系の単位ベクトル$${\bm{i'},\bm{j'},\bm{k'}}$$は時間変化することに注意)
$${\bm{L}}$$を時間微分すると
$${\dfrac{d\bm{L}}{dt}=\dfrac{d}{dt}(L'_x\bm{i'}+L'_y\bm{j'}+L'_z\bm{k'}) }$$
$${=\dfrac{dL'_x}{dt}\bm{i'}+\dfrac{dL'_y}{dt}\bm{j'}+\dfrac{dL'_z}{dt}\bm{k'} +L'_x\dfrac{d\bm{i'}}{dt}+L'_y\dfrac{d\bm{j'}}{dt}+L'_z\dfrac{d\bm{k'}}{dt} }$$
←$${\dfrac{d\bm{i'}}{dt}=\bm{ω'}×\bm{i'}、\dfrac{d\bm{j'}}{dt}=\bm{ω'}×\bm{j'}、\dfrac{d\bm{k'}}{dt}=\bm{ω'}×\bm{k'}}$$ を代入
$${=\dfrac{dL'_x}{dt}\bm{i'}+\dfrac{dL'_y}{dt}\bm{j'}+\dfrac{dL'_z}{dt}\bm{k'} +L'_x\bm{ω'}×\bm{i'}+L'_y\bm{ω'}×\bm{j'}+L'_z\bm{ω'}×\bm{k'}}$$
$${=\dfrac{dL'_x}{dt}\bm{i'}+\dfrac{dL'_y}{dt}\bm{j'}+\dfrac{dL'_z}{dt}\bm{k'}+L'_x(ω'_x,ω'_y,ω'_z)×(1,0,0)}$$
$${+L'_y(ω'_x,ω'_y,ω'_z)×(0,1,0)+L'_z(ω'_x,ω'_y,ω'_z)×(0,0,1)}$$
$${=\dfrac{dL'_x}{dt}\bm{i'}+\dfrac{dL'_y}{dt}\bm{j'}+\dfrac{dL'_z}{dt}\bm{k'}+L'_x(ω'_z\bm{j'}-ω'_y\bm{k'})+L'_y(-ω'_z\bm{i'}+ω'_x\bm{k'})}$$
$${+L'_z(ω'_y\bm{i'}+ω'_x\bm{j'})}$$
$${=\begin{bmatrix}\dfrac{dL'_x}{dt}\\\\\dfrac{dL'_y}{dt}\\\\\dfrac{dL'_z}{dt} \end{bmatrix}=L'_x\begin{bmatrix}0\dfrac{}{}\\\\ω'_z\dfrac{}{}\\\\-ω'_y\end{bmatrix}+L'_y\begin{bmatrix}-ω'_z\dfrac{}{}\\\\0\\\\\dfrac{}{}ω'_x\end{bmatrix}+L'_z\begin{bmatrix}ω'_y\dfrac{}{}\\\\-ω'_x\dfrac{}{}\\\\\dfrac{}{}0\end{bmatrix}}$$
→$${\bm{L'}=\begin{bmatrix}L'_x\\L'_y\\L'_z\end{bmatrix}=\begin{bmatrix}I'_x\:0\:\:0\\\:0\:\:I'_y\:0\\\:0\:\:0\:\:I'_z\end{bmatrix} \begin{bmatrix}ω'_x\\ω'_y\\ω'_z\end{bmatrix}=\begin{bmatrix}L'_xω'_x\\L'_xω'_y\\L'_xω'_z\end{bmatrix} }$$
よって$${L'_x=I'_xω'_x、L'_y=I'_yω'_y、L'_z=I'_zω'_z}$$
$${\dfrac{dL_x'}{dt}=I'_x\dfrac{dω'_x}{dt}、\dfrac{dL_y'}{dt}=I'_y\dfrac{dω'_y}{dt}、\dfrac{dL_z'}{dt}=I'_z\dfrac{dω'_z}{dt}}$$ を代入
$${=\begin{bmatrix}I'_x\dfrac{dω'_x}{dt}\\\\I'_y\dfrac{dω'_y}{dt}\\\\I'_z\dfrac{dω'_z}{dt}\end{bmatrix}+I'_xω'_x\begin{bmatrix}0\dfrac{}{}\\\\ω'_z\dfrac{}{}\\\\-ω'_y\end{bmatrix}+I'_yω'_y\begin{bmatrix}-ω'_z\dfrac{}{}\\\\0\dfrac{}{}\\\\\dfrac{}{}ω'_x\end{bmatrix}++I'_zω'_z,\begin{bmatrix}ω'_y\dfrac{}{}\\\\-ω'_x\dfrac{}{}\\\\\dfrac{}{}0\end{bmatrix}}$$
$${=\begin{bmatrix}I'_x\dfrac{dω'_x}{dt}-(I'_y-I'_z)ω'_yω'_z\\\\I'_y\dfrac{dω'_y}{dt}-(I'_z-I'_y)ω'_zω'_x\\\\I'_z\dfrac{dω'_z}{dt}-(I'_x-I'_y)ω'_xω'_y\end{bmatrix}=\begin{bmatrix}N'_x\\\\\\N'_y\\\\\\N'_z \end{bmatrix}}$$
記号を整理して
$${I_x\dfrac{dω_1}{dt}-(I_y-I_z)ω_2ω_3=N_1}$$ (4.1)
$${I_y\dfrac{dω_2}{dt}-(I_z-I_x)ω_3ω_1=N_2}$$ (4.2)
$${I_z\dfrac{dω_3}{dt}-(I_x-I_y)ω_1ω_2=N_3}$$ (4.3)
$${I_x,I_y,I_z}$$:主慣性モーメント
$${\bm{ω}=\begin{bmatrix}ω_1,ω_2,ω_3\end{bmatrix}}$$:角速度ベクトル
$${\bm{N}=\begin{bmatrix}N_1,N_2,N_3\end{bmatrix}}$$:力のモーメント
以上が静止座標系O-xyzからみた$${\dfrac{d\bm{L}}{dt}}$$を慣性主軸系O-$${\bm{x}_1\bm{x}_2\bm{x}_3}$$で表した式である。固定軸のある場合の運動方程式$${I\dfrac{d\bm{ω}}{dt}=\bm{N}}$$と比べて左辺第2項が付加されたものとなる。Eulerの運動方程式という。
5 角速度ベクトルωの慣性主軸系での動き
では、各瞬間での剛体の回転軸$${\bm{ω}}$$が剛体上をどう動きまわるかを考えよう。
剛体に外力が働かないとして$${N_1=N_2=N_3=0}$$すると、Eulerの運動方程式(4.1-3)の右辺は0となるから
$${I_x\dfrac{dω_1}{dt}=(I_y-I_z)ω_2ω_3}$$ (5.1)
$${I_y\dfrac{dω_2}{dt}=(I_z-I_x)ω_3ω_1}$$ (5.2)
$${I_z\dfrac{dω_3}{dt}=(I_x-I_y)ω_1ω_2}$$ (5.3)
ここで3つの主慣性モーメントのうち2つが等しい場合(地球)を考える。
(地球の慣性モーメント)
$${I_x=I_y=0.329587Mr_o^2 < I_z=0.330673Mr_o^2}$$である。
($${M}$$:地球の質量、$${r_o}$$:地球の半径)
$${I_x=I_y}$$を(5.3)に代入して
$${I_z\dfrac{dω_3}{dt}=(I_x-I_x)ω_1ω_2=0}$$ よって $${\dfrac{dω_3}{dt}=0}$$
積分して $${ω_3=一定=n}$$(5.4) 、 (5.1)(5.2)に代入
$${\dfrac{dω_1}{dt}=\dfrac{I_x-I_z}{I_x}nω_2}$$ (5.1')、 $${\dfrac{dω_2}{dt}=\dfrac{I_z-I_x}{I_x}nω_1}$$ (5.2')
(5.1')をtで微分して(5.2')を代入
$${\dfrac{d^2ω_1}{dt^2}=\dfrac{I_x-I_z}{I_x}n\dfrac{dω_2}{dt}=\dfrac{I_x-I_z}{I_x}n\dfrac{I_z-I_x}{I_x}nω_1=-\bigg(\dfrac{I_z-I_x}{I_x}n\bigg)^2ω_1}$$
これは単振動の方程式である。
$${I_z>I_x}$$のとき
$${ω_1=a\cos\bigg(\dfrac{I_z-I_x}{I_x}nt+α\bigg)}$$ (5.5-1)
(5.1')に代入して
$${ω_2=a\sin\bigg(\dfrac{I_z-I_x}{I_x}nt+α\bigg)}$$ (5.5-2)
$${I_z<I_x}$$のとき
$${ω_1=a\cos\bigg(\dfrac{I_x-I_z}{I_x}nt+α\bigg)}$$ (5.6-1)
(5.1')に代入して
$${ω_2=-a\sin\bigg(\dfrac{I_x-I_z}{I_x}nt+α\bigg)}$$ (5.6-2)
(5.5-1)(5.5-2)、(5.6-1)(5.7-2)より $${ω_1^2+ω_2^2=a^2}$$
(5.4)$${ω_3=n}$$ と併せると
角速度ベクトル$${\bm{ω}}$$の先端は慣性主軸系O-$${\bm{x}_1\bm{x}_2\bm{x}_1}$$上で座標(0,0,n)を中心とした半径$${a}$$の円周上を動くことがわかる。この角速度ベクトル$${\bm{ω}}$$の軌跡の円錐面をポルホード錘(polhode cone)と呼ぶ。(pol=極、hode=道)
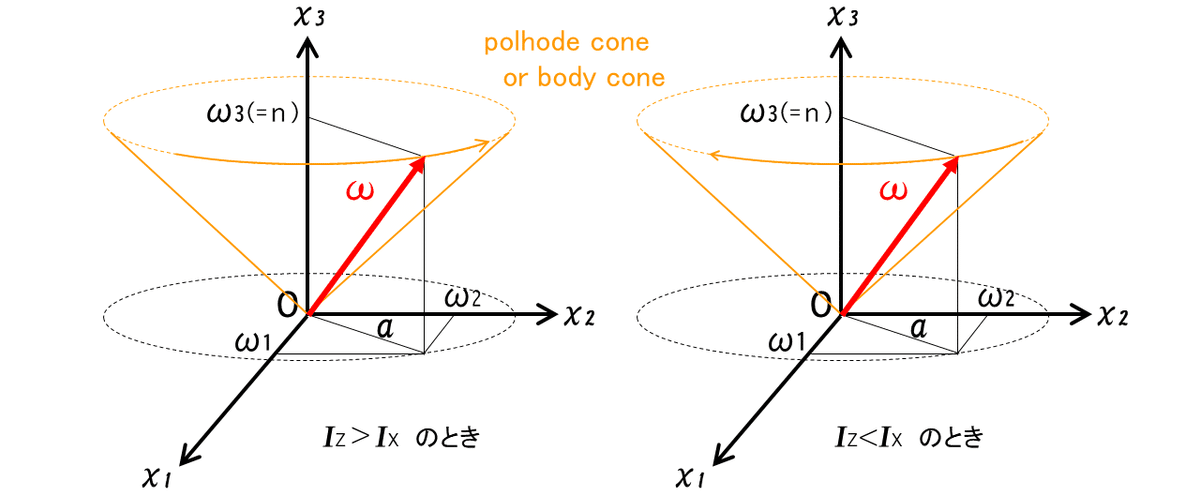
更に角速度ベクトル$${\bm{ω}}$$を中心に剛体は回転している。地球の運動にあてはめると(左側の図)、地軸が歳差運動をしながら地軸を中心に日周運動していることに相当する。
6 静止座標系から見た角運動量ベクトルと慣性主軸系
ところで
$${\bm{L}=\bm{I}\bm{ω}=\begin{bmatrix}L_1\\L_2\\L_3\end{bmatrix}=\begin{bmatrix}I_x\:0\:\:0\\\:0\:\:I_y\:0\\\:0\:\:0\:\:I_z\end{bmatrix} \begin{bmatrix}ω_1\\ω_2\\ω_3\end{bmatrix}=\begin{bmatrix}I_xω_1\\I_xω_2\\I_xω_3\end{bmatrix}}$$
これを図で表わすと

$${\bm{L}}$$と$${\bm{ω}}$$の$${x_1x_2}$$平面への射影は同一直線上にある。
よって$${\bm{L}}$$、$${\bm{ω}}$$、$${x_3}$$軸は同一平面内にあることがわかる。
ここで $${\tan{α}=\dfrac{a}{ω_3}}$$、$${\tan{β}=\dfrac{I_xa}{I_zω_3}=\dfrac{I_x}{I_z}\tan{α}}$$
$${I_z>I_x}$$の時
$${\tan{β}=\dfrac{I_x}{I_z}\tan{α}<\tan{α}}$$、$${β<α}$$
$${\bm{L}}$$(静止座標系のz軸)は$${x_3}$$軸と$${\bm{ω}}$$の内側にある。$${\bm{ω}}$$は$${\bm{L}}$$(z軸)のまわりを回り、
$${x_3}$$軸は$${\bm{L}}$$(z軸)を挟む$${\bm{ω}}$$の反対側の同一平面にあり$${\bm{L}}$$のまわりを回る。
$${I_z < I_x}$$の時
$${\tan{β}=\dfrac{I_x}{I_z}\tan{α}>\tan{α}}$$、$${β>α}$$
$${\bm{L}}$$(=z軸)は$${x_3}$$軸と$${\bm{ω}}$$の外側にある。$${\bm{ω}}$$は$${\bm{L}}$$(z軸)のまわりを回り、
$${x_3}$$軸は$${\bm{L}}$$(z軸)と$${\bm{ω}}$$のつくる平面の延長上にあって$${\bm{L}}$$のまわりを回る。

物体に固定された慣性主軸系O$${x_1x_2x_3}$$から見ると、$${\bm{L}}$$も$${\bm{ω}}$$も$${x_3}$$軸のまわりを角速度$${\dfrac{I_x-I_z}{I_x}n}$$で歳差運動をする。
一方、静止座標系Oxyzから見ると、$${\bm{ω}}$$も$${x_3}$$軸(慣性主軸系)も$${\bm{L}}$$(z軸:静止座標系)のまわりを回ることがわかる。$${\bm{L}}$$のまわりで$${\bm{ω}}$$のつくる円錐面をハーポルホード錘(herpolhode cone)と呼ぶ。
終わりに
この章はかなり手強かった。時間もかかった。
固有ベクトル、固有値、対称行列の対角化など初めて知ったことも多い。
ここに書いた以外にも3つの回転角(θ、φ、ψ、Euler角)を使った静止座標系⇔慣性主軸系の座標変換、$${\bm{ω}(=\bm{\dot{θ}}+\bm{\dot{φ}}+\bm{\dot{ψ}})}$$の両座標系での成分表示とpolhode cone、herpolhode coneなど手こずったがここでは書かない。まあ、次に進むことにしよう。
