
基礎理論
◯基数変換
私たちは普段10進数というものを利用しています。0から9まで順に進んでいき、そこから1桁繰り上がって10となる、これを10進数といいます。もっとかみ砕いていうと10進数というのは0~9までの数字しか使えません。なので9の次は10になるというわけです。小学生のころから当たり前のように使っているので、今更何を言っているんだと思うかもしれませんが、実はコンピュータの世界では10進数ではなく2進数というものを使っています。つまり全てのプログラムは0と1で成り立っているのです。また4進数は2²進数と置き換えることができるので、4や8や16進数を使う場合もあります。
基数とは位が上がる数字のことを指します。例えば私たちの身近にある10進数の基数は10です。なぜなら9から次の10になった時に1の位から10の位に上がるからです。基数nで表した数字を「n進数」と呼びます。
では2進数ではどのように位は上がるのでしょうか。コンピュータで使われる2進数では0と1だけの世界です。0、1の次は2ではなく位が上がって10となります。同様に8進数では「0、1、2、3、4、5、6、7」の世界なので7の次は8ではなく10になります。また16進数では「0、1、2、3、4、5、6、7、8、9、A ,B ,C ,D ,E ,F」を用いてFの次は10になります。実際に表にするとこういう風に数が進んでいきます。

数字を見ただけではどの進数か区別できない場合があるので
100(2)、111(8)、100(10)
のようにカッコをつけて区別します。
基本情報技術者試験では進数の変換を求める問題が出題されます。実際に例題を解いてみましょう。



◯基数変換(少数)
私たちが日常生活で利用している10進数では小数点以下の位はどのようになっているでしょうか。

位が10上がった時と同じ仕組みになっています。なので2進数や8進数、16進数の時も仕組みは同じです。

ではこちらも同じように例題を解いてみます。

こちらは過去に実際に出題された問題になります。
◯基数変換(10進数からn進数)
では10進数から他の進数に戻すときはどのように計算したらいいのでしょうか。n進数への変換は÷nをしていき、あまりを反対から並べることで求めることができます。それでは例題を解いてみます。

では少数の場合はどうなるでしょうか。こちらは先ほどとは逆にn進数への変換は×nをしていき、整数に繰り上がった数字を並べることで求めることができます。それでは例題を解いてみます。

基数変換すると永遠に少数が0にならないことがあります。これは無限小数(循環小数)だからです。例えば0.2(10)を2進数に変換しようとすると
0.001100110011…と0011が繰り返されます。つまり2の-n乗で表せないということです。
◯2進数、8進数、16進数の関係
8は2×2×2、16は2×2×2×2なのでそれぞれ簡単に変換することができます。
2進数→8進数:3桁ずつ分割して10進数へ変換
8進数→2進数:各桁を2進数に直して3桁にする
2進数→16進数:4桁ずつ分割して10進数へ変換
16進数→2進数:各桁を2進数に直して4桁にする
これは少数の場合も同じです。小数点から3桁もしくは4桁と考えて変換します。

◯補数
2進数ではマイナスは補数を用いて表現します。補数には「1の補数」と「2の補数」という2通りの表し方があります。
1の補数:ビットを全て反転して表します。つまり0→1、1→0とします。
元の数字が「01011101」(=64+16+8+4+1=93)の時
1の補数は「10100010」となり、これが-93を表します。
2の補数:1の補数の最小桁に1を足したものです。戻すときは反転してから1を足します。
元の数字が「01011101」(=64+16+8+4+1=93)の時
2の補数は「10100010+1=10100011」となり、これが-93を表します。
こちらの2つでは特に2の補数が重要とされており、詳しくは言いませんが理由としては、1の補数を足したときは全ての桁が1となりますが、2の補数の場合は最上位が1で他全ては0になるからです。
◯2進数の少数
2進数の世界で少数を表す際は2通りの方法があります。
固定小数点:数値を決まった大きさ(8ビット、16ビット、32ビットなど)、小数点の位置を固定して表します。また最上位ビットは符号ビットとする場合があり、0なら正、1なら負の数を表します。また負の数の時は「2の補数」表示となりますので、10進数に変換するときは反転して1足す作業が必要です。

浮動小数点:符号ビット、指数部、仮数部で表し、
数値=仮数×基数の指数乗
で計算します。限られたバイトの中で非常に大きな値や小さな値を表現できるので、数値計算の分野ではよく使われます。

浮動小数点形式では非常に広い範囲の実数を扱うことができますが、範囲内全ての数値を表現できるわけではないので誤差が生じます。
①桁あふれ誤差:計算結果が表現できる範囲から外れている場合に生じます。例えば8ビットで符号なしの場合、表現できる範囲は「00000000〜11111111」ですが、11111111に1を足した場合は100000000となり9桁になってしまうので8ビットで表現できません。最大値を超えることをオーバーフロー、最小値を超えることをアンダーフローと言います。
②まるめ誤差:切り捨てや切り上げ、四捨五入などにより指定された桁数に収めるために発生する誤差です。
③けた落ち:ほぼ等しい2つの数の引き算をした時に有効桁数が減ることで発生します。
④情報落ち:絶対値の大きな値と小さな値の加減算で発生します。『1兆1円持っている時にいくら持ってるか、と聞かれても1兆円持ってると言う』ように小さい値の情報が無視されることで生じる誤差です。
⑤打ち切り:円周率3.14159265…を3.14として計算しなさいと言うように、計算処理を途中で打ち切ることで発生する誤差です。
◯シフト演算
シフト演算とは桁を右や左にずらすことで掛け算割り算をする方法です。例えば10進数の場合、左に1桁ずらすのは10を掛けたのと同じになり、右に1桁ずらすのは10で割ったのと同じになります。つまりn進数の数字で左にxずらすということはnのx乗掛けたのと同じになり、右にyずらすということはnのy乗割ったのと同じになります。例題を解いてみましょう。
例題1
①10010×32
32は2⁵なので左に5桁ずらすのと同じ。よって答えは1001000000
②1001001÷16
16は2⁴なので右に4桁ずらすのと同じ。よって答えは100.1001
③2進数のある数xに次のアクションをしたとき、xの何倍になるか
xを3ビット左にシフトし、それにxを足す。
3ビット左に増やすのは2³=8を掛けるのと同じ。
8x+x=9xになるので答えは4倍
シフトには符号を考えない論理シフトと符号を考慮する算術シフトがあります。
8ビット固定の論理シフトの時はあぶれたビットは捨てて、空いたビットには0を入れます。例えば00001100を左に2ビットずらすと00110000になります。また右に3ビットずらすと00000001となりますが桁溢れが発生し正しい値になりません。(上記の場合はアンダーフローとなる。)
8ビット固定の算術シフトの時は最上位ビットを符号ビットとしているとき、符号ビットは固定され、あぶれたビットは捨てて、空いたビットには左シフトの時は0、右シフトの時は符号ビットと同じ数字を入れます。
例えば10011100を左に2ビットずらすと11110000になり、右に2ビットずらすと11100111となります。
〇論理演算
論理演算とはコンピュータを構成する論理回路によって、論理式を実現したものです。基本となる論理演算には次の4つがあります。
・論理和:AとBどちらも0のときだけ「0」を出力する演算。

・論理積:AとBどちらも1のときだけ「1」を出力する演算。

・否定:0⇔1を反転する演算。1の補数と同じです。

・排他的論理和:AとBどちらか1のときだけ「1」を出力する演算。

計算するときにこちらの法則を覚えておくとスムーズに解ける場合もあるので覚えておくと便利です。

〇論理回路
論理計算の回路を組み合わせることにより、様々な機能を実現することができます。その中でも代表的なものが加算回路で、次の2種類があります。
・半加算器:桁上がりの数を考慮します。

・全加算器:入力に下位の桁からの桁上がりを含めます。

〇ビット演算
論理演算を使ってビットごとに計算することをビット演算と言います。「10110011」を論理演算でビットを反転させるにはどのように計算したらいいでしょうか。
答えは「11111111」と排他的論理和をすると「01001100」となり、元の2進数が反転します。
では下位4ビットのみ反転させるにはどうすればいいでしょうか。
答えは「00001111」と排他的論理和をすると、下位4ビットのみ反転されます。
このように論理演算をすることで様々なデータを取り出すことができます。試験でもよく出題されるので、覚えておきましょう。
「0」とEOR → そのまま
「1」とEOR → 反転
「0」とAND → 全部0
「1」とAND → そのまま
「0」とOR → そのまま
「1」とOR → 全部1
〇アナログとデジタル
アナログとは連続的に変化、なめらかに変化する情報のことを指します。このようなデータだと、0か1しか認識できないコンピュータでは処理ができないので、飛び飛びの値のデジタルに直す必要があります。変換には次の3つのステップがあります。
・標本化(サンプリング):アナログ信号の波形を一定の時間間隔で測定。サンプリング回数が多ければ多いほどアナログデータに近づきます。1秒間で10回測定する場合、サンプリング周波数10Hzと表す。
・量子化:一定の間隔に区切り数値化すること。段階数が多ければ多いほどアナログデータに近づきます。
・符号化:量子化された値を2進数に変換すること。

〇制御技術
コンピュータの制御には次のような技術があります。
・フィードバック制御:外部環境の情報を入手し、その結果から修正動作を行います。例として温度を温度センサから、携帯の角度をジャイロセンサなどから入手し、モーターなどアクチュエータと呼ばれる信号を力に変化して操作する機械で制御します。
・フィードフォアード制御:予測をもとに動作をします
・シーケンス制御:あらかじめ定められた順序または条件に従って制御の各段階を逐次決めていく方法です。
〇オートマトン
オートマトンとはコンピュータの状態と遷移をモデル化したものです。
・状態遷移図:オートマトンの状態の遷移を図にしたものです。下の図は自動販売機で100円のジュースを販売中のものを表しています。終了状態ありのオートマトンを有限オートマトンといいます。

・状態遷移表:オートマトンの状態の遷移を表にしたものです。

〇AI(人工知能)
AIとは人が行うような学習・認識・予測・判断などの知的な活動をコンピュータにさせる取り組みやその技術のことです。AIは様々なことができますが、空気を読んだり、0から何かを生み出すことはできません。AIを利用するためには機械学習が必要になります。
・教師あり学習
ラベル(答え)付きデータを大量に渡し、比較することで判断できるようにすることです。
・教師なし学習
データを大量に渡し、分類(クラスタリング)することで判断できるようにすることです。
・強化学習
システム自身が試行錯誤しながら最適なシステム制御を実現することです。
・ディープラーニング(深層学習)
ニュートラルネットワークを用いた機械学習です。人の神経細胞(ニューロン)をモデル化したものを利用しています。
〇線形代数
機械学習には、大量のデータをまとめて処理し簡潔に書き表すことができる行列やベクトルの知識と概念があると便利です。
スカラー:大きさを表す、実数のことです。
ベクトル:スカラを一列に並べたものです。
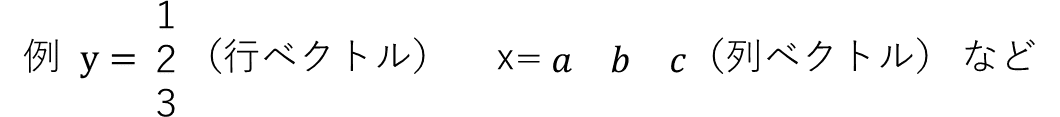
行列:行ベクトルと列ベクトルが組み合わさったものをいいます。

・行列の計算



掛け算の場合、行列Aの列と行列Bの行が同じでないと計算できません。2行3列の行列と3行2列の行列は計算できますが、4行2列の行列とは計算できないです。「a行b列の行列」と[b行c列の行列」の積は、「a行c列の行列」になります。

形が正方形の行列を正方行列といいます。n行n列の正方行列をn次の正方行列といったりもします。また左上から対角線上が1、それ以外が0の正方行列を単位行列といいます。特徴として行列Aと単位行列の積は行列Aと変わりません。
〇確率

例えばさいころを1回ふって1が出る確率は、さいころを1回ふって起こりうる場合の数は[1,2,3,4,5,6]の6通り、1が出る確率は1通りなので1/6となります。
・順列
異なるn個のものから、r個取り出して並べる場合の数です。
※!は階乗を表し、1ずつ小さい整数を、1まで順に掛けた数のことです。
例 5!=5×4 × 3×2 ×1 =120

・組み合わせ
異なるn個のものから、並び順を考慮せずにr個取り出す方法の数です。

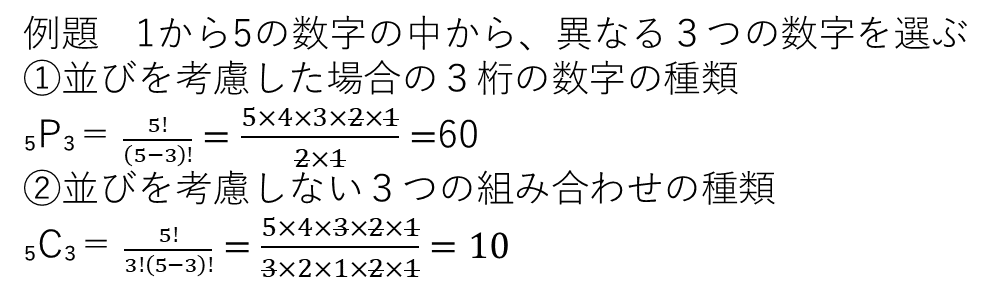
〇統計
データを集めて全体の傾向を割り出すものを統計といいます。例でいうとテストの平均、日本の平均年収などが当てはまります。
平均値:データ合計/データ個数
中央値(メジアン):データを並べたときに中央にある値のことです。中央が偶数個の場合は2つの平均値をとります。極端に高い、低い値があると影響を受けます。
分散:平均値からのばらつきを表す指標です。分散が大きければ大きいほど、ばらつきが多いということです。それぞれのデータをx、データ個数をnとすると次のような式になります。

標準偏差:分散を平方根にとることによって計算される値です。平均を中心に大体の数が入っているエリアを表すことができます。

モード:出現頻度の最も高い値のことです。
レンジ:データの最大値と最小値の差です。
正規分布:平均値、中央値、モードが一致し、平均値から標準偏差±σの間に約68%が、±2σの間に約95%のデータが入るきれいな分布のことです。

この記事が気に入ったらサポートをしてみませんか?
