純粋戦略と混合戦略

今回は中級者〜上級者の方に向けて、GTOにおいて純粋戦略と混合戦略の差を述べていこうと思います。
内容が難しいので、私のこれまでのnoteは一通り読んできてください。
また、内容の難しさは論理的な難しさに起因しており、pokerの実力には関係しません。
勉強への意欲と、投げやりにならずに1行ずつ読む気持ちがあれば誰でも理解可能な内容です。

既にわかっている！という方も自分の理解に誤解がないのか、確認していただける内容にはなるかと思いますのでよろしくお願いします。

・Nash's theorem (Nashの定理)

さて、こちらは見慣れたUTG-6max-cashのopenレンジです。(6max-cashとは6人で行うリングゲームのこと)

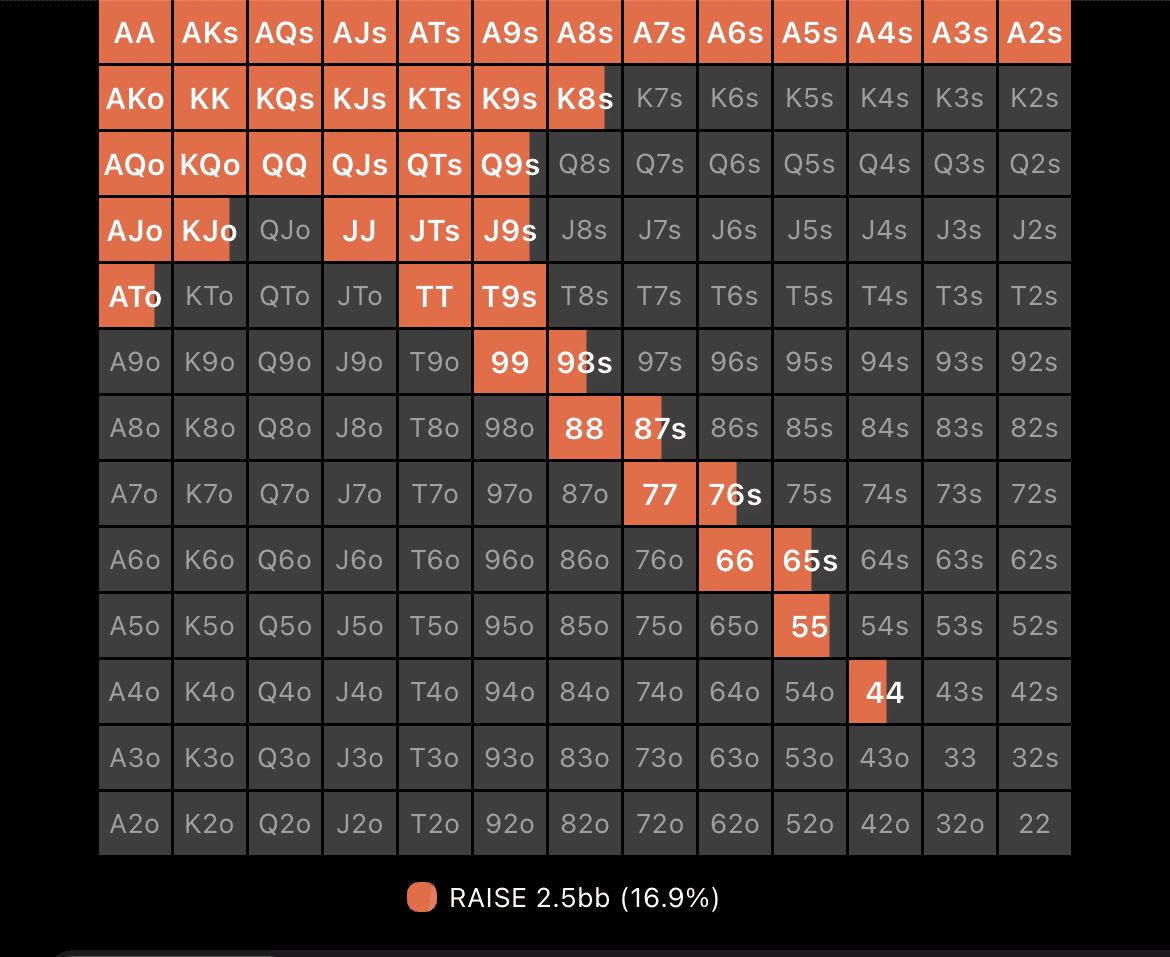
UTGは2.5bbで色のついた部分をopenしますが、その下限のハンドを見てみると「中途半端に色がついているもの」がありますね。これは、全四角のうち色のついている比率でopenしなさい。ということです。このように2種類以上の戦略から、確率で戦略を選択するような方法を混合戦略といいます。

そういえば、よく言うNash均衡という言葉を説明してませんでしたね。今後の為にここで述べておきましょう。

少し数学的な話になりますが厳密な構成に拘らず、伝えたいことを掻い摘んで話します。
あまり読み飛ばさずに読んでください。

ポーカーを含む基本的なゲームでは、
(有限ゲームの混合拡張など理論的な話はありますが、少し簡単に説明させてください。)
ブラウアーの不動点定理という数学の定理から、Nashの定理と呼ばれるものが導かれます。

こちらの理論を説明するには位相空間(大学数学の分野)に関する知識が必要で、当記事で説明をする気はありませんが、Nashの定理自体は有用です。

Nashの定理
混合戦略を許せば基本的なゲームはNash均衡をもつ

Nash均衡とはなんでしょうか？
ポーカーのようなゼロサムゲームにおいて、
AさんがGTO戦略S1をBさんがGTO戦略S2をとっているとします。
この時の
(S1,S2)
という戦略の組み合わせがナッシュ均衡になっています。
もう少し正確にはNash均衡とは、
各プレーヤーが自身の戦略のみを変更しても利得が上昇しないような戦略の組み合わせ
を指します

少し難しいですね。伝えたいことを整理するので理解できているかを確認してください。

---1つ目---
2人ゼロサムゲームにおける、Nash均衡とは
2人のプレーヤーがそれぞれGTO戦略を取る状態であるということ。
言い換えれば、GTO戦略とは2人ゼロサムゲームにおいて、Nash均衡のうち1方の戦略を指している
ということ

---2つ目---
"基本的なゲーム"において、Nash均衡が存在することは数学の定理によって
混合戦略を用いることで存在する
と証明されていること。

大丈夫そうですか？

以下の良くある問題に答えられればOKかと思います。

「私はNash均衡をプレーしている！」という発言は正しいでしょうか？
→Nash均衡とは戦略の組に対する言葉です。相手がGTO戦略を取らないとき、自分がGTO戦略をとっていたとしてもNash均衡とはなりません。

「2人がGTO戦略を取る時、Nash均衡になっている」という発言は正しいでしょうか？
→2人でのゲームにおいて、正しいです。というかNash均衡が先に定義されていて、その時の各プレーヤーの戦略をGTOと呼んでいます。

さて、なぜいきなりNash均衡の話をしたかと言いますと。

GTO戦略はNash均衡から来ていて、
Nash均衡は混合戦略により担保されている
よって、
GTO戦略において混合戦略とは極めて重要なファクターである

と言うことを強調したかったからです。

混合戦略の話をする時、
「ああ、敵に戦略がバレないように色んなプレーをすることでしょ！」
というような発想の人がいますが、混合戦略とはもっと根源的で重要なものです。
先の意見が確実に間違いとまでは言いませんが、このような発言をする人は総じて認識が甘いです。

実際最初に見たレンジ表の通り、GTOで混合戦略が採用されていることが見てとれますね！

・混合戦略とは

では実際に混合戦略の特徴についてお話ししていきます。

さて、あなたはGTO戦略を用いてプレーをしています。
もう少し言えば、相手はかなり強く、あなたに対するMESをプレーしています。
つまり両者がGTO戦略を取っていてナッシュ均衡が成立している状態です。

対照的に、このときあなたのGTO戦略は相手のGTO戦略に対して、MESとなっているはずですね？
(このことを意識してください！)

そのような特性を持つGTO戦略において混合戦略を取るハンドがあります。
UTGopenレンジの55をイメージしてください。
(冒頭に画像がありますので、覚えていない人は確認してくること！)

この55という混合戦略を取る一つのハンドに注目して考えてみましょう。
あなたがUTGで55を配られた時、openとFoldどちらのEVが高いでしょうか？

solver+の戦略を見る限り55は8割くらいはopenしているようですね。
ということはopenの方が期待値が高いですか？
それとも、EVは計算できるものではない！というのが直感的な答えですか？

正解は、
混合戦略における各アクションでEVは必ず同じ
となります。

仮に、一方のアクションが高いEVを持つとしましょう。
するとGTO戦略からそのアクションをより高頻度でとるようにした"GTO改戦略"はGTO戦略より高いEVを持ちますね？
GTO戦略がMESであると言う前提に矛盾します。

この、
混合戦略でEVは同じ
と言う結論を"絶対に"覚えていてください。

間違えても、「GTOだとopenした方が期待値高いよ」と言うような発言に惑わされないように。
youtubeやSNSで発信している人ですらこのようなお粗末な意見を主張している人がいます。

さて、ここで疑問を持った方はいませんか？
「EVが同じなら純粋戦略で良くないか？なぜ混合戦略なんかを使うのか」
実はこれが冒頭の議論につながってきます。

・混合戦略とExploit

混合戦略はGTOをGTOたらしめるものであったはずです。では実際にどこでその力が発揮されているのでしょうか？

GTOには
ナッシュ均衡においては自身の戦略のみを変えてもEVを向上させることができない
という定義からくる
GTOはGTOに対するMESである
という議論のほかにも次の性質があります。

このナッシュ均衡という定義を相手から見た際に、相手側も戦略を変更してEVを向上できません。
すなわち再三申し上げていますが
GTOはExploitされない戦略
となっています。

どのようにしてこの素晴らしい2つの性質
・GTOはGTOへのMES
・GTOはexploitされない
を共存させているのでしょうか？
その秘密が混合戦略なのです

結論として、
複雑な混合戦略を守ることでGTOはExploitされない戦略となっている
ということですね。

ここまでの理論の展開を理解できたでしょうか？
整理していきます。

まず初めに、
「Nash均衡」という単語を定義しました。
この「Nash均衡」は「混合戦略」により数学的に存在が担保されており、実はGTOは「Nash均衡」の片割れをさしていました。

次に我々は
Nash均衡の性質から得られる、
「あなたのGTOが相手のGTOに対するMESとなっている」
という事実に基づき、
「GTOから戦略を変更し、EVを向上させる方法はない」
為に、
「GTOで混合戦略を取る時、各アクションのEVは必ず等しい」
という結論を得ました。
これが1つ目の混合戦略におけるpoint
「混合戦略でEVは同じ」
です。

最後に、今度はNash均衡の性質を相手側から見ることで、
「GTO戦略はExploitされない」
という事実を確認しました。
この素晴らしい性質を守るのが混合戦略です。すなわち、2つ目のpointは
「混合戦略を守ることでExploitされない」
ということです。

網掛け部分の理論展開がわかっていること、太字部分を強烈に理解していること。
ここまで確認ができれば、あなたは混合戦略を(十分なレベルで)誤解なく理解していると言えると思います。

「これがわかると何が嬉しいの？」という方へ向けて、応用を記載していきましょう。

・混合戦略の理解からくる応用

ここまでご覧くださった方であれば、以下のような疑問を持つのではないでしょうか？

・Exploitをしているつもりでも、相手がGTOを取っていたら自分だけEVを失ってしまいそうで怖い

・相手がどういったプレーヤーのときにGTO戦略でなく、Exploit戦略を採用すればよいのかわからない

このような疑問に対して今回座学が生きてきます。

・まず1つ目のような状況を考えてみましょう。

あなたの左側には
「GTO的なプレーはできるが、Exploit戦略をその場で構築するだけの技術はないだろうし、あってもしてこないだろう」
と想定されるGTOマシーンが座っています。
そのさらに左には
「超フィッシュ！プリフロップはめちゃめちゃ参加率が高い！ポストフロップは絶対コールしかしないしワンペアなければ確実に降りてくれる！2ペア以上できると喜んで立ち上がってくれるから丸わかり！最高！」
という人がいます。

あなたはより多くのハンドでこのフィッシュとぶつかりたいですが、レンジを広げてGTOマシーンにレイズされるとかなり厳しいですね…

このような時、混合戦略を取るハンド全てで100%参加することがとても素晴らしい適応となります。
混合戦略の比率はまちがえておりますが、GTOマシーンにEVlossをするようなことはありません。
さらに、フィッシュと対戦機会は増え、EVを多く稼げます。

・次に2つ目のような状況を考えてみましょう。

あなたが対戦している相手は純粋戦略をめちゃめちゃにまちがえていると想定できます。
しかし、そのレンジはとても想像がつかなく、23oや27oでall-inしたときもあれば、QQで4倍レイズ参加してきて、相手の3betにハンドを見せながらフォールドしていました。

このような、GTOとあまりに乖離しているが戦略が全く読めない相手に対しては、「Exploitしなくては！」と焦る人が多いですが、GTO戦略をプレーするだけでも十分だと思います。

相手が純粋戦略をミスする場合、そのミスにより失ったEVはこちらがGTO戦略をとっているだけで全て入ってきます。
Exploitになっているかもわからない適応をするくらいならこのEVを享受しましょう。

逆に、
極めてGTO的だが、混合戦略において頻度の薄いプレーを連発してくると思われるプレーヤー
に対してはアグレッシブにExploitする必要があります。
相手は混合戦略の比率がおかしいというリークを抱えているのに、こちらがGTOのままではEVは変わりません。
相手のミスにつけ込み、EVをむしり取りましょう。
ここが、上手いプレーヤー同士の勝負どころです。

このように、混合戦略と純粋戦略の意味を理解することはとても大切です。
誤った情報に踊らされず、しっかりとした知識をつけましょう。

実戦では、Exploit戦略を適切に立てれるプレーヤーはほとんどいませんから、混合戦略を守る必要性はそこまで高くありません。
Exploitする際には、まず混合戦略の比率を変えること、GTO相手には純粋戦略ミスをしないこと。
意識していきましょう！

ちなみに、混合戦略比率を守る際には、50%でレイズのハンドで前回foldしたから今回はレイズ！とやるのは誤りです。
前回のアクションと今回のアクションは独立に決める必要があります。
時計の秒針の位置
目に入った数字の下一桁
適当に思い浮かべた数字から複雑な演算をした後の割り算による余り
などでアクションを、決めるのが良いと思います。
なるべく簡単に乱数が取れる方法を考えておきましょう

・最後に

ご存知の方も多いかと思いますがTwitterをしています。noteとも連携したので良ければそちらもご覧ください。

前回までの記事、コンスタントにスキやフォロー、お布施が来ています。とても感謝しています。ありがとうございます。

購入してくださった方が、記事の感想をTwitter上で引用により発言してくれているのを見ると、本当にモチベーションになります。
誤植のご連絡もいただき、助かります。

これからもチマチマ更新していくのでよろしくお願いします。

記事は基本無料ですが、価値があると判断くださった方、よければ紹介、スキやフォロー、お布施をよろしくお願いします。