さっくりデータ構造_03//木

ポホヨラの村人A

2022年9月5日 21:14

　第三回目、さっくりデータ構造です。
　話のネタと言うか、話す順番がなんか取っ散らかってわけわかんなくなり始めてきましたが、気張って行くどー。（空元気）

前回

1.グラフ

　コンピューターの世界にはグラフと言うものがあります。と言っても一般的な折れ線グラフやら棒グラフのことではありません。次みたいな感じの図形の事です。

　なんかこう、地図の目的地を道で結んだかのような形をしています。グラフを扱う離散数学の世界は中々恐ろしいものがるので、あんまり詳しく突っ込みません。火傷するので。

　まず、グラフにはざっくり二つの要素がございます。それは頂点（バーテックス、vertex）と辺(エッジ、edge)です。
　
　大体こんな感じ。

　ちょっと見にくくて申し訳ございません。頂点がデータが格納されたりして、そのデータどうしの関係を結ぶのが辺と言った感じでしょうか。

　さて、では取り合えずこのグラフを扱いやすくするために番号を振り割ってみましょう。

　頂点に取り合えず番号をふりました。ただしこれだけでは実装して扱うのは少し難しそうです。なので、この番号を使って上手くグラフを表現する方法を考える必要があります。

　グラフを扱う方法には二つあります。それは行列とリストです。それぞれに利点と欠点があります。

・行列
　利点：アクセス速度が速い
　欠点：必要となるメモリ数が頂点数二乗となる

・リスト
　利点：アクセス速度が隣接する辺の数だけあり、遅い
　欠点：必要メモリが、頂点数＋辺の数と比較的少ない

　ちょうどトレードオフの関係となっています。この辺りは利用目的によって良い感じに使い分けていく感じでしょうか。

取り合えずイメージ図を見てみましょう。

　上記の行列が、グラフを行列表現に変換したものとなります。　

　それぞれの行と列が頂点を表しているものと考えてください。この時、右上から左下にかけた対角成分は自分自身に帰ってきていることが分かるかと思います。こういった自分自身に返る性質は反射律(離散数学をやってる方はなじみ深いかもしれませぬ。xRxになるあれです)っぽいです。この行列ではあえて2と表現していますが、まあ、普通は1にします。

　で、この表の見方は、行、列、好きな方の番号に注目した時に、辺が繋がっている頂点を1、繋がってない頂点を0で表現しています。例えば左横の4に注目して横方向に見た時に、2,3,6,7との交点に１がついているかと思います。つまり、(4,2),(4,3),(4,6),(4,7)に辺が繋がっていることを示しています。

　また、行列の特徴として、辺が一方通行でなければ、対角成分を中心軸にして、綺麗に対照的な形になっています。例えなら、(1,1)から(7,7)の軸に折って、折紙のように閉じると、1と0の部分が綺麗に重なるようなイメージでしょうか。

　では、次にリストを使った表現を見てみましょう。

　　こちらはグラフをリスト表現に変換したものとなります。

　リストの入口が、それぞれの頂点を表現していると考えてください。その頂点からエントリーして、一つずつ次のデータへと辿って行きます。これを順番に辿って行くと、最終的にはnullへと辿り着きます。

　それぞれの頂点に繋がっているデータがちょうど隣接する頂点となります。つまり、辺の数＋２データがリストにぶら下がっている形になります。

　また、縦の頂点をリストにように束ねる事も出来ます。そうすると、動的にデータを繋げやすいので、新しくグラフを更新しやすかったりしています。

　また、見ての通り、データにアクセスしようとすると、態々順繰りにデータを辿って行かないといけないので、データへのアクセス速度がそこそこ遅くなってしまうのが難点です。

　はい、という訳で蛇足でした。うん、ごめんなさい。直接木構造とは関係なかったりします。ただ、木構造はグラフの一部なので一応頭に入れておいて損は無いかと思います。

木

　で、本題の木のお話です。グラフの中で、特定の特徴を持つものを木と言います。まず、一番の特徴はグラフが閉路を持たないことです。

　閉路とは何かというと、文字通り閉じてる路のことで、頂点と辺で面を構成している、とか、丸で囲むことができる部分が存在する状態の事です。

　はい、こんな感じで頂点と辺で囲まれている部分を閉路ですね。別の言い方をすると、くるっと回って元々の位置に帰ることができるってことです。因みに右と左の塊が繋がっていませんが、こんな感じのグラフも一応あったりします。

　では実際に閉路の無いグラフを見てみましょう。

　閉路が無いグラフの一例です。このグラフは木の構造を持っているのですが、このままでは、何故木と呼ばれているのかよくわかりませんね。という訳で、ここで、親と書かれている点に注目してこれを整理してみましょう。

　はい、少しは木っぽく見えましたでしょうか。中々特徴的な形をしていますよね。木構造では、頂点から下の方へ幾つかの辺が伸び、上から下に順繰りに伸びていくような形になっています。この構造が、データを扱う際、有益に働くことが有ります。

　木にはほかにも次のような性質があります
・（頂点ー１）本の辺を持つ
・全てが連結である
・どれか一本の辺を取ると、二つに分かれてしまう
・特定の二点間辺と頂点経由して必ずたどり着くことができる
・新しく一本辺を加えると閉路が出来る

　因みに、この幾つかの気が散らばっているグラフのことを森と呼んだりもします。次の様な感じ。

　では、ここから木に関する用語を見ていきましょう。

　まず木の見方として、ある頂点に注目して、他の頂点との関係から名前を付けられます。この名前は家系図的な名前になっています。上記の図では主に右側の部分です。

親：注目点の上に上にある頂点。
子供：注目頂点の下にある頂点。
孫：注目頂点の二つ下にある頂点。子供の子供の頂点。
兄弟：同じ親を共有する頂点。
祖先：親の親の頂点。

　まさに、ザ・家系図みたいな命名規則、まあ、この辺は特に戸惑うことは無いと思います。

　次に、木構造全体を見た時のパーツに付けられている名前です。上記の図の左側ですね。

根：木の一番上。親のいない頂点。
葉：木の一番下の頂点。子供のいない頂点。
内部：根でも親でもない頂点。
部分木：木の中に含まれている木。

　木は再帰構造的に作られていて、木の下に木がくっついています。その、木の中にはまた木があって、と頂点単位になるまで繰り返すことができます。ですので、木の中に含まれる木を態々部分木と呼ぶんですね。

　最後に、木に含まれている頂点の位置の数え方に関する名前です。木は根から必ず辿ることができますが、この時何個頂点を経由したかが重要だったりします。この距離の事はそれぞれ次のように呼びます。

深さ：ある頂点から下向きに経由した時、何個頂点を経由したのかを示す言葉。
高さ：ある頂点から上向きに経由した時、何個頂点を経由したのかを示す言葉。

　例えば現在地を０として考えると、青色の注目点から見た時高さは2ですし、子供への深さへは2になります。ですので、この木全体の高さ、または深さは全体で４になる訳ですね。

　で、木の中にはいくつか種類がありまして、その種類は基本的に頂点が最大で何個子供を持てるかによって呼び名が変わってきます。

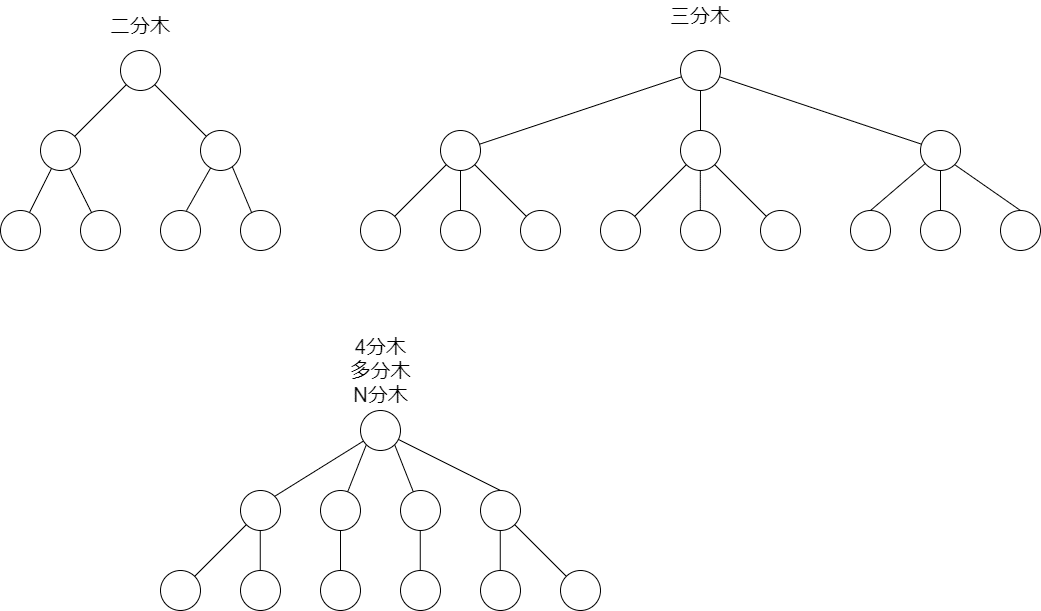
　頂点を子供に二つ持っていると二分木、三つ持っていると三分木など、N分木と言う呼び方をしていきます。あんまりに多い時には多分木と読んだりもします。シンプルですね。

3.実装

　では、実際にこの木を実装してみましょう。木構造を作るときは、リストや配列では中々辛いものがあります。ヒープと言う配列で木を扱う構造もあったりしますが、まあ、これはそこそこ面倒なので飛ばしていきましょう。

　大まかな構造はこんな感じですね。一つのデータに親、右、左、もっと必要であれば追加で、データのポインタを保管します。基本的には上から辿って行きますが、上に辿って行くこともできます。

　はい、では簡単にコードに起こしてみます。

#include<iostream>

class Node {
	int data;
	Node* Parent, *Left, *Right;
public:
	Node(int num) { data = num; Parent = NULL; Left = NULL; Right = NULL; }
	void SetLeft(Node* left) { left->SetParent(this); this->Left = left; }
	void SetRight(Node* right) { right->SetParent(this); this->Right = right; }
	void SetParent(Node* parent) { this->Parent = parent; }
	Node* GetLeft() { return Left; }
	Node* GetRight() { return Right; }
	Node* GetParent() { return Parent; }
	int GetData() { return data; }
};

void SearchTree(Node* node) {
	if (node == NULL)	return;
	std::cout << node->GetData() << " ";
	SearchTree(node->GetLeft());
	SearchTree(node->GetRight());
}

int main() {
	//_CrtSetDbgFlag(_CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF);

	Node node_1(1), node_2(2), node_3(3), node_4(4), node_5(5), node_6(6), node_7(7);

	node_1.SetParent(NULL);
	node_1.SetLeft(&node_2);
	node_1.SetRight(&node_3);
	node_2.SetLeft(&node_4);
	node_2.SetRight(&node_5);
	node_3.SetLeft(&node_6);
	node_3.SetRight(&node_7);

	SearchTree(&node_1);
	std::cout << std::endl;
	SearchTree(&node_2);
	std::cout << std::endl;
	SearchTree(&node_3);

	return 0;
}

結果

1 2 4 5 3 6 7
2 4 5
3 6 7

　一応これで木は構成できていますが、どうなっているのかは分かりにくいですね。再帰を使った深さ優先探査といった手法で探索を行っていますが、まあ、この辺りについてはその内出てきます。ですので、ここでは実際に木が構成されているかどうかだけ確認しましょう。

　実際の木の状態は右のようになっています。これを読み込む順番が辺の隣にある数字になります。親、左、右の順番で読み込むため、１の左の２、２の左の４、子供がいないので２に戻り、２の右の子供の５、子供がいないので、２から１へと戻り、右の３へ移動、３から子供の左の６へ移動して戻り、今度は３の右の７へと移動します。

　以上、非常に簡単ですが、木構造の説明でした。

3.結び

　木構造はデータやグラフの探索方法などに使用されたり、何らかの状態のパターン（ボドゲとか）を表現したり、構文木の生成など中々に応用が多い構造となります。

　データの整理を行うソートの計算量が最善でnlognになる事の説明などに使われたりしていて、中々に奥深いものです。

　説明下手でしたが、以上となります。お疲れさまでした。

この記事が気に入ったらサポートをしてみませんか？