
作者の説明する【無下限呪術】が意味不明だったので数学的に正しい内容を考える
(先日、居酒屋でバンギャと呪術廻戦の話題でレスバになりました)
僕「無下限呪術はアキレスと亀じゃないでしょ」
バンギャ「いや作中でアキレスと亀って明記されてるよ」
僕「だってアキレスと亀は収束しちゃうし速度が変わらないでしょ」
バンギャ「だから収束する術式って作中で言ってるじゃんww0を分割すると速度が落ちるんだよw」
僕「……(絶句)」
1.最初に
負けたので書きました。
レスバの後、単行本のオマケに無下限呪術についての解説が記載されていると聞き、購入したところ、衝撃の真実が記載されていました(筆者は今までジャンプで読んでた)。内容を要約すると以下の通りです。
・術式の内容は「アキレスと亀」
・0を分割することで負の自然数が出来る、それによって速度が遅くなる
・「負の数」ではなく「負の自然数」とした理由は、よくわからない物の根拠をよくわからない物にしておいた方が、皆「ま、いっか」となるから。
・一応の根拠としては、S = 1/2 + 1/4 + 1/8・・・を全部数えた人はいないから、その中に「負の自然数」がないとは言い切れない。
あのさぁ……もうめちゃくちゃだよぉ……0を分割しても負の数なんて現れないよぉ……そもそも負の自然数なんて概念存在しないよぉ
どうりでバンギャにレスバで勝てないわけです。だってバンギャは公式設定に則った正しい主張をしており、数学に準拠してないのは作者だったんですから……
それに対して数学的な矛盾をいくらついても、野暮な揚げ足取り男になるだけでしょう。まるで身投げと変わらない。そんなレスバだったのです。
しかし、このままだとあまりに悔しいので、陰キャオタク全開のキモい文章で自慰行為をすることにしました。以上が本記事を書くに至った経緯です。
前置きが長くなりましたが、
「単行本のオマケにて記述された説明を全て無視し、無下限呪術を数学的に正しい解釈で、尚且つ原作の描写に矛盾が無いよう説明しよう」
という挑戦が本記事の趣旨です。ですので、芥見下先生の解釈とはまるで違う、完全自己満足な内容になっている点を予めご了承ください。
また、筆者の専攻は数学では無いため、本記事では大学レベルの数学は用いません。よって数学が苦手な方でも理解出来る内容になっていますので、その点はご安心ください。
2.作中描写
まず、作中で描写された無下限呪術の情報に対して筆者の解釈を叙述していき、最終的に数学を用いて説明すべき、術式の内容を定義します。
(1)アキレスと亀

69話において、五条悟は上記のように術式を説明しています。本記事では、この「アキレスと亀」を、無限に到達できないことの例え話と解釈し、術式の内容とは関係無い描写だと考えます。
その結論に至った根拠を以下に示しますが、まず「アキレスと亀」を知らない方のために簡単な説明を記述します。
【アキレスと亀の概要】
瞬足のアキレスが、ノロマな亀と駆けっこをすることになりました。

最初に亀がいる位置をBとします(図①)。アキレスがBに到達したとき、亀は少し先の地点Cにいます(図②)。アキレスがCに到達したときに、また亀は少し先の地点Dにいます(図③)。 これをいくら繰り返しても、亀は常にアキレスより前にいるはずです。つまり、アキレスは永遠に亀に追いつけないことになります。
【解説】
この思考実験ではアキレスと亀は常に一定の速度であり、減速はしません。ですので結論、アキレスは亀に追いつけます(当たり前ですが)。無限和は必ずしも無限に発散するわけではなく、今回のような場合は収束します。つまり、追いかけた距離を無限に足し上げても(AB+BC+CD・・・)答えは無限にならず、有限の値(アキレスが亀に追いつくまで移動した総距離)が求められます。適当な数字を入れて計算してみると分かりやすいと思うので、以下に簡単な例を記載しておきます。
【例1】

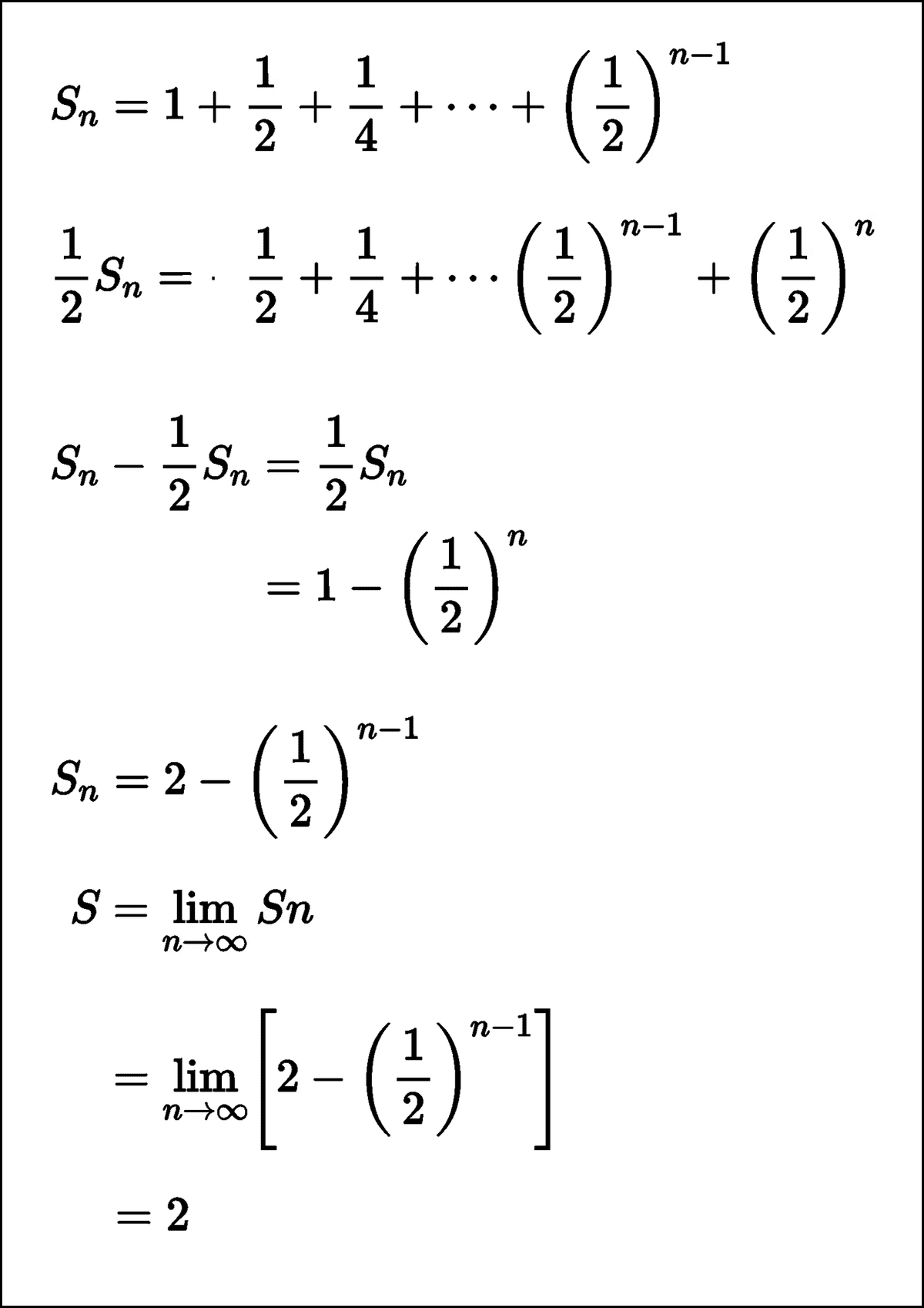
よってアキレスは2m走ることで亀に追いつきます。
「無限に足してるのに答えが2に収束するのはおかしい!答えも無限になるはずだ!」
と、思われた方のために更に例を記載します。
【例2】
長方形の面積を無限級数で求める。

果たして長方形の面積は無限になるでしょうか?なりませんよね。
1(縦の長さ)×2(横の長さ)=2(面積)
やはり、2に収束することが分かります。
つまり、アキレスと亀は面白い思考実験ですが、結局のところアキレスが追いつくまでの距離(もしくは時間)を無限回の足し算で求めているにすぎません。
以上のことから、「アキレスと亀」では無下限呪術は再現できません。
この手の説明をすると
「現実にはあり得ないアキレスと亀を、術式で再現するのが無下限呪術なんでしょ」という反論があるかと思いますので、以下に続きます。
(2)収束についての言及
「無限」の力で創る 絶対不可侵の空間。無下限の下では、接近物は永久に近づく”収束”のみ。五条家相伝の「無下限呪術」は、無限を現出し接触を阻むバリアだ。
引用元:『呪術廻戦』ファンブック
「接近物は永久に近づく”収束”のみ」という記述は「アキレスと亀」と矛盾します。前述の通り、収束するのであればアキレスは亀に必ず追いつくからです。よって「現実には起こり得ないアキレスと亀を術式で再現している」のような仮説は否定されます。
なぜなら「現実には起こり得ないアキレスと亀を術式で再現している」=「現実では収束するアキレスと亀を術式で発散させている」になるので、その場合「接近物は永久に近づく”発散”のみ」という記述になるべきだからです。
(3)速度についての言及
「アキレスと亀」は速度が変化しません。アキレスが減速するから亀に追いつけないという話ではなく、距離を無限に分割した時、無限和は収束するのか発散するのかという話でした。ですので「アキレスと亀」を術式で再現しても「近づくほど遅くなる」という結果は得られません。
(1)~(3)より、本記事では「アキレスと亀」は無限に到達できないことの例え話と解釈し、術式の内容とは関係無い描写だと考えます。
(4)無限級数についての言及

「収束する無限級数」という情報が追加されました。これにより(2)で指している「収束」が数列ではなく級数のことだと確定します。
負の自然数という意味不明なセリフに対しては考察を行いません。このセリフは五条悟の言い間違いと捉えるのが極めて自然であり、他の解釈をすることが不可能だからです。

これまでの情報をまとめると
・速度は距離に比例して減速する
・無限級数(何の無限和かは不明)を収束させる術式
となり、この2点から
①無下限呪術は相手の総移動距離(無限級数)を収束させる術式。必然的に速度は0に収束する。
②無下限呪術は速度の無限級数を収束させる術式。必然的に速度は0に収束する。
という2つの解釈が出来るように見えます。どちらも整合性のある仮説に一見すると思えますが、実は違います。①は数学的に不自然な内容になっています。
まず、①がどういう意味かを説明します。自転車を想像してください。その自転車を無限の時間を用いて走らせます。その際、自転車の進んだ距離が有限の値をとる(無限にならない)とき、自転車は減速して途中で止まったと考えるしかありません。では、進んだ距離よりも遠い場所に五条悟がいた場合、自転車はいつか五条悟に到達できるのでしょうか?無理ですよね、無限の時間があっても到達できなかったのですから。
これが、「総移動距離(無限級数)を収束させると、必然的に速度は0に収束する」の意味です。この仮説の趣旨自体は正しいのですが、総移動距離=無限級数という点が間違っています。例として、初速が1の減速する自転車で考えてみましょう。

というのが①の内容になるのですが、これは誤りです。上記の計算をグラフで表してみましょう。

y軸を速度、x軸を時間とした時、距離はグラフの面積によって表せます。上図の塗りつぶした領域が、先ほど無限級数で求めた総移動距離(面積)です。
これは、おかしいですよね。総移動距離がグラフの面積を明らかに超えています。正しくは下図のようになります。

このような面積は、速度の関数を積分をすることで求められます。速度が変化するとき、移動距離を求める際は積分を用いるのが一般的で、無限級数を用いるのは誤りです。今回の場合、f(x)を0から∞の区間で広義積分し、自転車の移動距離を求めるのが正しいアプローチです。よって、①の仮説は不適切であり、本記事では五条悟の術式を
②無下限呪術は速度の無限級数を収束させる術式。必然的に速度は0に収束する。
と定義付けます。
3.数学的な説明
前章で、
②無下限呪術は速度の無限級数を収束させる術式。必然的に速度は0に収束する。
が作中の描写と矛盾しないことを示しました。
本章では、②が数学的に正しいこと、無下限呪術の内容を再現できることを示していきます。
(1)数学的に正しいことの証明
高校数学で習う範囲に以下の公式があります。

この公式は
無限級数が収束する時、数列の極限(n→∞)は0に収束するという意味です。(逆は成立しません)。この公式から②無下限呪術は速度の無限級数を収束させる術式。必然的に速度は0に収束する。は数学的に正しいと言えます。
(2)無下限呪術を再現できることの証明
②の意味を簡単に説明します。まず、自転車を無限の時間を用いて走らせます。その際、一定時間ごとに速度を測定し、集計します。集計した速度を全て足し合わせた値が有限の(無限にならない)とき、自転車は減速して途中で止まったと考えるしかありません。
この際、進んだ距離<五条悟との距離
であれば、自転車は永遠に五条悟に到達できないことになります。
これが②の意味であり、「俺の術式は収束する無限級数、俺に近づくモノはどんどん遅くなって、結局俺まで辿り着くことは無くなるの」を満たしています。
今回の場合、速度の変化を表す数列に対して極限(∞)をとっているので、収束するまでに無限の時間が必要になりますが、距離が有限の値なら問題ありません。目視では確認できない(止まっているように見える)速度になるまでの減速なら一瞬でしょう。結局、移動距離(積分の値)<五条悟までの距離、となる値を五条悟が変数に設定しますからね。
つまり、
変数xを持つ
常に広義積分(0→∞)に有限の値を持つ
常に収束する無限級数(関数)
を提示できれば、②で無下限呪術を再現できると証明できます。
以下に示します。

この関数について叙述し始めると無限に長くなるので、詳しくは書きません。x>1 において、常に収束する無限級数だということ、xに何を代入しても1/n^xは広義積分(0→∞)に有限の値を持つということだけ理解してください。非常に面白いので、興味がある方は是非調べてみてください。
この関数の存在により、②で無下限呪術を再現できると証明できました。
【結論】無下限呪術はゼータ関数を用いて速度の無限級数を収束させる術式。必然的に速度は0に収束する
以下、術式順転「蒼」と術式反転「赫」についても記述しますが、原作に数学的な描写、解説が乏しいため、正直どうとでも解釈できます。ですので、内容も薄く、自信のある解釈でも無いので、オマケ程度に読んでいただけたら幸いです。(虚式「茈」に関しては記述すらしていません)
・術式順転「蒼」

無限を生む・止める力の無下限術式を負の呪力で強化すると、対象を”引き寄せる力”となります。”-1個のリンゴ”のような虚構を生むことで、指定した場所に敵を吸い込む反応を作ることが出来る。
ゼータ関数の符号を負にすると、速度はマイナスになります。これを物理学では逆ベクトルへの速度と解釈しますが、これが0に収束する場合、引き寄せる力と解釈することも可能です。逆ベクトルへの速度が0に向かうということは五条悟方向へ加速しているという見方が出来るからです。
・術式反転「赫」

術式反転「赫」とは、反転術式で生んだ正の力を無下限の術式に流すことで発動する技。無限を発散するため、術式順転「蒼」とは正反対の”弾く力”となるのが特徴。
ゼータ関数に1を代入すると(関数の定義を無視しているので正確な表現ではない)、無限級数は発散します。有名な調和級数ですね。意図的に関数のルールを破ることで発散を作り出すことは可能です。x<0 を設定した場合は、無限の加速を表す関数になり、ベクトルさえ指定できれば弾く力を生み出すことができます。
4.最後に
ご精読ありがとうございました。高校卒業してから殆ど数学に触れてなかったので、記事内にミスが多数あると思われます。見つけたら教えてください。
ここまで書いといてなんですが、筆者は別に呪術廻戦のファンではありません。というか無下限呪術にいたっては嫌いです。現実世界に無限は存在しませんからね。期待値のパラドックス(サンクトペテルブルクのパラドックス)とかをどや顔で語ってる人を見ると悲しい気持ちになります。
ですから、そこまで熱量を持って書き始めた記事では無く……正直後半から辛かったです。最初はゼータ関数の証明まで記述しようと思ったんですが止めました。自己満足に首を絞められ、逃げるようにペンを置きました。
もしバンギャと再度レスバをする機会があれば

と、ドヤ顔で記事を読ませたいと思います。
この記事が気に入ったらサポートをしてみませんか?
