A Formal Derivation of the Leading-Order Calculation of GTMDs
注意:この記事は私が書いた原案をo1-previewに渡して書いてもらった記事です。たまに間違えるのでいくらか修正してる箇所があります。が、私が間違えてる場合もあります。式の導出は自分でやったのでo1がちゃんと出せるかは知らないです。内容はQFTの基本を触った人ならわかると思います。
Abstract
In this article, we present a detailed derivation of the leading-order calculation of quark generalized transverse momentum-dependent distributions (GTMDs) in quantum chromodynamics (QCD). Starting from the definition of GTMDs, we perform explicit calculations using perturbation theory, focusing on the leading-order contributions from the quark correlator. The derivation involves the manipulation of quark and gluon propagators and the application of standard techniques in quantum field theory (QFT). We aim to provide a clear and comprehensive guide for researchers and students interested in the theoretical foundations of GTMDs.
Introduction
Generalized transverse momentum-dependent distributions (GTMDs) are fundamental objects in QCD that provide comprehensive information about the three-dimensional partonic structure of hadrons. They unify and generalize both generalized parton distributions (GPDs) and transverse momentum-dependent distributions (TMDs), serving as powerful tools to study the correlations between the transverse position and momentum of partons inside hadrons.
In this article, we perform a formal derivation of the leading-order (LO) calculation of quark GTMDs. We start from the standard definition of GTMDs and proceed through a step-by-step calculation using perturbative methods. Our goal is to elucidate the technical aspects of the derivation, making it accessible to readers with a background in QFT and perturbative QCD.
Definition of GTMDs
We begin with the quark GTMD correlator:
$$
\begin{aligned}
&W^{[\Gamma]}_{\Lambda'\Lambda}(P,x,\bar{ k}_\perp,\Delta,n_-;\eta) \\
&=\frac{1}{2}\int d\bar k^-\!\int\frac{d^4z}{(2\pi)^4}\,e^{i \bar k\cdot z}\,\langle p'\,\Lambda'|\overline\psi(-\tfrac{z}{2})\Gamma\,\mathcal W_{n_-}\psi(\tfrac{z}{2})|p\,\Lambda\rangle ,
\end{aligned}
$$
where:
$${P=\frac{p+p'}{2}}$$is the average momentum of the initial and final hadron states.
$${Δ=p′−p}$$ is the momentum transfer.
$${\bar k}$$ is the average quark momentum.
$${\Gamma}$$ denotes a Dirac matrix that projects onto specific quark spin structures.
$${\mathcal{W_{n_-}}}$$ is a Wilson line along the light-cone direction $${n_}$$ to ensure gauge invariance.
$${Λ,Λ′}$$ are the helicities (spin projections) of the hadron states.
Neglecting the Wilson Line Contribution
In our calculation, we neglect the contribution of the Wilson line $${\mathcal{W}_{n_-}}$$ in the expansion of the GTMD. This simplification can be justified in the light-cone gauge, where the component $${A^+ = 0}$$ (with $${A^\mu}$$ being the gluon field). In the light-cone gauge, the path-ordered exponential in the Wilson line reduces to unity along the light-cone direction $${n_-}$$, effectively removing the Wilson line from the correlator:
$$
\mathcal{W}_{n_-} = \mathcal{P} \exp\left( -i g_s \int_{- \infty}^0 d\lambda\, n_- \cdot A\left( \lambda n_- + x \right) \right) = 1.
$$
This simplification allows us to focus on the quark field dynamics without the complication of the Wilson line. It is important to note that neglecting the Wilson line is specific to the light-cone gauge and may not be applicable in other gauges where the Wilson line can have a non-trivial contribution.
Leading-Order Calculation
To perform the leading-order calculation, we consider the QCD action and expand the correlator to second order in the strong coupling constant $${g_s}$$.
QCD Action and Interaction Term
The QCD action is given by:
$$
\begin{aligned}
S= \int d^4 x \left[ \overline{\psi}(x) (\gamma^\mu (\partial_\mu -ig_s t^a A^a_\mu(x))) - m) \psi(x) -\frac{1}{4} G^a_{\mu\nu}(x) G^{a \mu\nu}(x) \right],
\end{aligned}
$$
where:
$${ψ(x)}$$ is the quark field.
$${A_μ^a(x)}$$ is the gluon field.
$${D_μ=∂_μ−ig_s t^a A_μ^a(x)}$$ is the covariant derivative.
$${G_{μν}^a(x)}$$ is the gluon field strength tensor.
$${m}$$ is the quark mass.
$${t^a}$$ are the generators of the SU(3) color group.
The interaction term relevant at leading order is:
$$
\begin{aligned}
S_{int} = -ig_s \int d^4 x, \overline{\psi}(x) \gamma^\mu \psi(x) t^a A^a_\mu(x) .
\end{aligned}
$$
Expansion of the GTMD Correlator
At leading order, we expand the GTMD correlator to include two insertions of the interaction term:
$$
\begin{aligned}
W^{[\Gamma]}_{\Lambda'\Lambda} &= \frac{1}{2} \int d\bar{k}^- \int \frac{d^4 z}{(2\pi)^4} \, e^{i \bar{k} \cdot z} \, \langle p', \Lambda' | \overline{\psi}\left(-\tfrac{z}{2}\right) \Gamma\, \mathcal{W}_{n_-} \psi\left(\tfrac{z}{2}\right) | p, \Lambda \rangle \\ &= \frac{-g_s^2}{4} \int d\bar{k}^- \int \frac{d^4 z}{(2\pi)^4} \, e^{i \bar{k} \cdot z} \int d^4 x \int d^4 y \\ &\quad \times \langle p', \Lambda' | \overline{\psi}\left(-\tfrac{z}{2}\right) \Gamma\, \mathcal{W}_{n_-} \psi\left(\tfrac{z}{2}\right) \overline{\psi}(x) \gamma^\mu t^a \psi(x) A^a_\mu(x) \overline{\psi}(y) \gamma^\nu t^b \psi(y) A^b_\nu(y) | p, \Lambda \rangle.
\end{aligned}
$$
The negative sign arises from expanding the exponential of the interaction term and considering terms up to second order in $${g_s}$$.
Propagators and Contractions
Quark and Gluon Propagators
The free quark and gluon propagators are:
Quark Propagator:
$$
\begin{aligned}
\langle \psi(z)_i \overline\psi(y)_j \rangle_0 &= \Delta_F^{ij}(z-y) = i \int \frac{d^4q}{(2\pi)^4} e^{-iq (z-y)} \frac{(\gamma_\rho {q}^\rho+m)_{ij}}{q^2-m^2+i\epsilon},
\end{aligned}
$$
Gluon Propagator:
$$
\begin{aligned}
\langle A^a_\mu(z)A^b_\nu(y) \rangle_0 &= \delta^{ab} \Delta_F^{\mu\nu}(z-y) = i \delta^{ab} \int \frac{d^4q}{(2\pi)^4} e^{-iq (z-y)} \frac{d_{\mu\nu}(q)}{q^2+i\epsilon} ,
\end{aligned}
$$
with $${d_{\mu\nu}(q)}$$ depending on the gauge choice (e.g., in Feynman gauge, $${d_{\mu\nu}(q) = -g_{\mu\nu}}$$).
Changing Variables
We introduce impact parameter $${b}$$ and relative coordinates $${r}$$:
$$
\begin{aligned}
x=b+\frac{r}{2} , y=b-\frac{r}{2}
\end{aligned}
$$
Performing Contractions
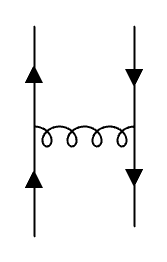
Using Wick's theorem, we consider the contractions that contribute at leading order:
$$
-2 \langle \psi\left(b + \tfrac{r}{2}\right) \overline{\psi}\left(-\tfrac{z}{2}\right) \rangle_0 \langle \psi\left(\tfrac{z}{2}\right) \overline{\psi}\left(b - \tfrac{r}{2}\right) \rangle_0 \langle A^a_\mu\left(b + \tfrac{r}{2}\right) A^b_\nu\left(b - \tfrac{r}{2}\right) \rangle_0.
$$
The factor of -2 arises from:
The negative sign due to the interchange of fermionic operators.
A combinatorial factor accounting for the two ways of contracting the quark fields.
Note: In this calculation, we only consider the contributions from the quark correlator to the leading-order expansion. There are additional contributions involving gluon correlators that can arise from contractions of all the quark fields. These gluon correlator contributions are omitted in this calculation for simplicity and to focus on the quark part. A complete leading-order analysis would include both quark and gluon correlator contributions.
Fourier Transform and Momentum Integrals
Evaluating the Contractions
We evaluate the contractions by performing the Fourier transforms of the propagators:
$$
\begin{aligned} I &= \int \frac{d^4 z}{(2\pi)^4} \, e^{i \bar{k} \cdot z} \, \Delta_F\left(b + \tfrac{r}{2} + \tfrac{z}{2}\right) \Gamma \Delta_F\left(\tfrac{z}{2} - b + \tfrac{r}{2}\right) \\ &= \int \frac{d^4 z}{(2\pi)^4} \, e^{i \bar{k} \cdot z} \, i \int \frac{d^4 q_1}{(2\pi)^4} \, e^{-i q_1 \cdot \left( b + \tfrac{r}{2} + \tfrac{z}{2} \right) } \, \frac{ \gamma_\rho q_1^\rho + m }{ q_1^2 - m^2 + i \epsilon } \, \Gamma \\ &\quad \times i \int \frac{d^4 q_2}{(2\pi)^4} \, e^{-i q_2 \cdot \left( \tfrac{z}{2} - b + \tfrac{r}{2} \right) } \, \frac{ \gamma_\sigma q_2^\sigma + m }{ q_2^2 - m^2 + i \epsilon }. \end{aligned}
$$
Simplifying the exponentials and integrating over $${z}$$, we get:
$$
\begin{aligned} I &= - \int \frac{d^4 q_1}{(2\pi)^4} \int \frac{d^4 q_2}{(2\pi)^4} \, e^{- i (q_1 - q_2) \cdot b - i (q_1 + q_2) \cdot \tfrac{r}{2} } \, (2\pi)^4 \delta^{(4)} \left( \bar{k} - \tfrac{ q_1 + q_2 }{2} \right ) \\ &\quad \times \frac{ \left( \gamma_\rho q_1^\rho + m \right ) \Gamma \left( \gamma_\sigma q_2^\sigma + m \right ) }{ \left( q_1^2 - m^2 + i \epsilon \right ) \left( q_2^2 - m^2 + i \epsilon \right ) }. \end{aligned}
$$
Change of Variables
We introduce new variables:
$$
q_1 = \bar{k} + \frac{\Delta}{2}, \quad q_2 = \bar{k} - \frac{\Delta}{2},
$$
where $${\Delta = q_1 - q_2}$$.
Substituting back, we have:
$$
I = - \frac{1}{(2\pi)^4} \int \frac{d^4 \Delta}{(2\pi)^4} \, e^{- i \Delta \cdot b - i \bar{k} \cdot r } \, \frac{ \left( \gamma_\rho \left( \bar{k}^\rho + \tfrac{ \Delta^\rho }{2} \right ) + m \right ) \Gamma \left( \gamma_\sigma \left( \bar{k}^\sigma - \tfrac{ \Delta^\sigma }{2} \right ) + m \right ) }{ \left( (\bar{k} + \tfrac{ \Delta }{2} )^2 - m^2 + i \epsilon \right ) \left( (\bar{k} - \tfrac{ \Delta }{2 } )^2 - m^2 + i \epsilon \right ) }.
$$
Application of the Translation Operator
To simplify the matrix elements involving the fields at different positions, we use the translation operator in quantum field theory. The translation operator relates the field at position $${x}$$ to the field at the origin:
$$
O(x) = e^{ i \hat{P} \cdot x } O(0) e^{ - i \hat{P} \cdot x },
$$
where $${\hat{P}}$$ is the momentum operator.
Applying the Translation Operator
Using the translation operator, we shift the fields to the origin:
$$
\begin{aligned} \overline{\psi}\left( b + \tfrac{ r }{ 2 } \right ) &= e^{ i \hat{P} \cdot \left( b + \tfrac{ r }{ 2 } \right ) } \overline{\psi}(0) e^{ - i \hat{P} \cdot \left( b + \tfrac{ r }{ 2 } \right ) } , \\ \psi\left( b - \tfrac{ r }{ 2 } \right ) &= e^{ i \hat{P} \cdot \left( b - \tfrac{ r }{ 2 } \right ) } \psi(0) e^{ - i \hat{P} \cdot \left( b - \tfrac{ r }{ 2 } \right ) } . \end{aligned}
$$
Substituting back into the matrix element, we have:
$$
\begin{aligned} &\langle p', \Lambda' \vert \overline{\psi}\left( b + \tfrac{ r }{ 2 } \right ) \gamma^\mu \cdots \gamma^\nu \psi\left( b - \tfrac{ r }{ 2 } \right ) \vert p, \Lambda \rangle \\ &= e^{ i ( p' - p ) \cdot b + i \left( \tfrac{ p' + p }{ 2 } \right ) \cdot r } \langle p', \Lambda' \vert \overline{\psi}\left( \tfrac{ r }{ 2 } \right ) \gamma^\mu \cdots \gamma^\nu \psi\left( - \tfrac{ r }{ 2 } \right ) \vert p, \Lambda \rangle. \end{aligned}
$$
Noting that $${\Delta = p' - p}$$ and $${P = \tfrac{ p + p' }{ 2 }}$$, we can write the exponentials as:
$$
e^{ i \Delta \cdot b + i P \cdot r }
$$
Incorporating into the GTMD Expression
Substituting the translated matrix element and integrating over $${b}$$, we obtain:
$$
\begin{aligned} W^{[\Gamma]}_{\Lambda'\Lambda} =& - i \frac{1}{(2\pi)^4} \frac{ g_s^2 C_F }{2} \int d\bar{k}^- \int d^4 r \int d^4 b \int \frac{ d^4 \Delta }{ (2\pi)^4 } \, e^{ - i ( \Delta - ( p' - p ) ) \cdot b - i \bar{k} \cdot r } \\ &\quad \times \langle p', \Lambda' \vert \frac{ \overline{\psi}\left( \tfrac{ r }{ 2 } \right ) \gamma^\mu \left( \gamma_\rho \left( \bar{k}^\rho + \tfrac{ \Delta^\rho }{ 2 } \right ) + m \right ) \Gamma \left( \gamma_\sigma \left( \bar{k}^\sigma - \tfrac{ \Delta^\sigma }{ 2 } \right ) + m \right ) \gamma^\nu \psi\left( - \tfrac{ r }{ 2 } \right ) }{ \left( (\bar{k} + \tfrac{ \Delta }{ 2 } )^2 - m^2 + i \epsilon \right ) \left( (\bar{k} - \tfrac{ \Delta }{ 2 } )^2 - m^2 + i \epsilon \right ) } \vert p, \Lambda \rangle \\ &\quad \times \int \frac{ d^4 q }{ (2\pi)^4 } \, e^{ - i q \cdot r } \, \frac{ d_{\mu\nu}(q) }{ q^2 + i \epsilon }.
\end{aligned}
$$
The integral over $${b}$$ yields a delta function enforcing momentum conservation:
$$
\int d^4 b \, e^{ - i ( \Delta - ( p' - p ) ) \cdot b } = (2\pi)^4 \delta^{(4)} \left( \Delta - ( p' - p ) \right ).
$$
Using this delta function, we set $${\Delta = p' - p}$$ in the expression.
Simplifying the Expression
Combining Exponentials and Integrals
Combining the exponentials, integrating over $${\Delta}$$ and setting $${p'-p = \Delta}$$ again, we have:
$$
\begin{aligned} W^{[\Gamma]}_{\Lambda'\Lambda} =& - i \frac{ g_s^2 C_F }{2 } \int d\bar{k}^- \int d^4 r \int \frac{ d^4 q }{ (2\pi)^4 } \, e^{ - i ( \bar{k} + q ) \cdot r } \, \frac{ d_{\mu\nu}(q) }{ q^2 + i \epsilon } \\ &\quad \times \langle p', \Lambda' \vert \frac{ \overline{\psi}\left( \tfrac{ r }{ 2 } \right ) \gamma^\mu \left( \gamma_\rho \left( \bar{k}^\rho + \tfrac{ \Delta^\rho }{ 2 } \right ) + m \right ) \Gamma \left( \gamma_\sigma \left( \bar{k}^\sigma - \tfrac{ \Delta^\sigma }{ 2 } \right ) + m \right ) \gamma^\nu \psi\left( - \tfrac{ r }{ 2 } \right ) }{ \left( (\bar{k} + \tfrac{ \Delta }{ 2 } )^2 - m^2 + i \epsilon \right ) \left( (\bar{k} - \tfrac{ \Delta }{ 2 } )^2 - m^2 + i \epsilon \right ) } \vert p, \Lambda \rangle.
\end{aligned}
$$
Changing Variables
We perform a change of variables for the momentum $${q}$$:
$$
q \rightarrow q - \bar{k}.
$$
This simplifies the exponentials and denominators:
$$
e^{ - i ( \bar{k} + q ) \cdot r } \rightarrow e^{ - i q \cdot r }.
$$
The gluon propagator becomes:
$$
\frac{ d_{\mu\nu}( q - \bar{k} ) }{ ( q - \bar{k} )^2 + i \epsilon }.
$$
Final Expression for the GTMD
The GTMD correlator now reads:
$$
\begin{aligned} W^{[\Gamma]}_{\Lambda'\Lambda} =& - i g_s^2 C_F \int d\bar{k}^- \int \frac{ d^4 q }{ (2\pi)^4 } \, \frac{ d_{\mu\nu}( q - \bar{k} ) }{ ( q - \bar{k} )^2 + i \epsilon } \\ &\quad \times \frac{ \left[ \gamma^\mu \left( \gamma_\rho \left( \bar{k}^\rho + \tfrac{ \Delta^\rho }{ 2 } \right ) + m \right ) \Gamma \left( \gamma_\sigma \left( \bar{k}^\sigma - \tfrac{ \Delta^\sigma }{ 2 } \right ) + m \right ) \gamma^\nu \right ]_{ ij } }{ \left( (\bar{k} + \tfrac{ \Delta }{ 2 } )^2 - m^2 + i \epsilon \right ) \left( (\bar{k} - \tfrac{ \Delta }{ 2 } )^2 - m^2 + i \epsilon \right ) } W^{ ij }_{ \Lambda'\Lambda }( P, q ), \end{aligned}
$$
where we have defined the quark-quark correlator as:
$$
\begin{aligned} W^{ ij }_{ \Lambda'\Lambda }( P, q ) &= \frac{1}{2} \int \frac{ d^4 r }{ (2\pi)^4 } \, e^{ - i q \cdot r } \, \langle p', \Lambda' \vert \overline{\psi}\left( \tfrac{ r }{ 2 } \right )_i \psi\left( - \tfrac{ r }{ 2 } \right )_j \vert p, \Lambda \rangle \\ &= \frac{1}{2} \int \frac{ d^4 r }{ (2\pi)^4 } \, e^{ i q \cdot r } \, \langle p', \Lambda' \vert \overline{\psi}\left( - \tfrac{ r }{ 2 } \right )_i \psi\left( \tfrac{ r }{ 2 } \right )_j \vert p, \Lambda \rangle. \end{aligned}
$$
Conclusion
We have performed a formal derivation of the leading-order calculation of quark GTMDs by expanding the correlator to second order in $${g_s}$$ and carefully evaluating the quark and gluon propagators. In our calculation, we focused on the contributions from the quark correlator, omitting the gluon correlator contributions for simplicity. These gluon correlator contributions can be significant in certain processes and should be considered for a complete leading-order analysis.
The final expression involves a convolution over the quark and gluon momenta, encapsulating the dynamics of the quark-gluon interaction at leading order from the quark correlator perspective. This derivation provides valuable insights into the structure of GTMDs and serves as a foundation for further theoretical investigations. It also demonstrates the application of perturbative QCD techniques to compute observables relevant for understanding the internal structure of hadrons.
References
Quantum Field Theory Textbooks:
Peskin, M. E., & Schroeder, D. V. (1995). An Introduction to Quantum Field Theory. Addison-Wesley.
Itzykson, C., & Zuber, J.-B. (1980). Quantum Field Theory. McGraw-Hill.
GTMDs and QCD:
Meissner, S., Metz, A., & Schlegel, M. (2009). Generalized parton correlation functions for a spin-1/2 hadron. Journal of High Energy Physics, 2009(08), 056.
Diehl, M. (2003). Generalized parton distributions. Physics Reports, 388(2-4), 41-277.
終わりに
今回o1-previewを使って記事を書いてみましたが、原案では適当にしていた部分をちゃんと書いてくれて良い感じです。
数式を打ち込むのが面倒だと思っていたのですが、o1からコピペすると 簡易数式TeX数式簡易数式 のように簡易数式でTeXの数式が挟まれてる状態になっていることがわかりました。長い数式の場合 簡易数式\begin{aligned}数式\end{aligned}簡易数式 となっているのでより見つけやすくnoteへの変換も楽でした。
また、文献も情報があってるようでいい感じです。
元の導出の時にpropagatorに対しても演算子と同じTranslation作用すると勘違いしたりしましたが、演算子ではないので古典量と考えないといけないですね
私の原案を貼り付けておきます。とても雑ですね
今回の結果は次の論文に書いてある(97)式のクォーク部分と多分一致してるはず
