
QAP.09:4色問題(グラフの彩色問題)、AND制約とpenalty関数の使い方【量子コンピュータ/アニーリング@Python/Fixstars Amplify】
【はじめに】
「Fixstars Amplify」では、「ヘルパー関数」を使用することにより、裏でいい感じに「制約条件に対する数式化」等をしてくれる「制約条件オブジェクト」を作成できる。
※再掲:ヘルパー関数

※関連:第6回
今回は例題を通して「penalty関数」を使った「and制約」の使いどころを見ていく。
※penalty関数を用いた制約のドキュメントは以下参照
【例題】:東北6県の4色問題
今回は「Fixstars Amplify」の「オンラインデモサイト」にある「グラフ彩色問題」をベースに「もう少し小規模にした問題」やってみる。
問題:
東北6県について、隣接した県には同じ色を塗らないようにしつつ、できるだけ少ない色で塗り分けよう。
考え方:
「県をノード」、「隣接情報をエッジ」とした「グラフ理論:Graph theory」と考えていく。
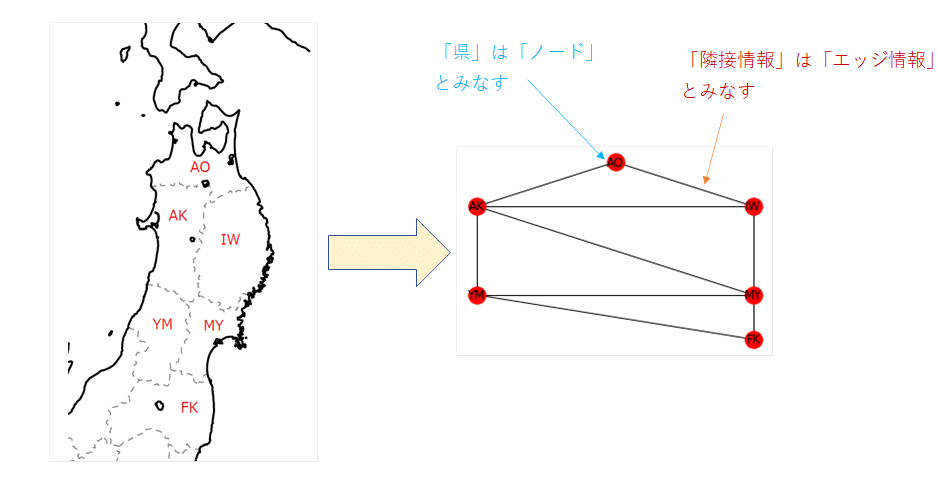
【解答例】
今回の実行環境は「Fixstars Amplify」+「Google Colab」。
【1】ライブラリのインストール
! pip install amplify
! pip install --upgrade amplify【2】クライアントオブジェクトの作成
from amplify.client import FixstarsClient
client = FixstarsClient()
client.parameters.timeout = 1000 # タイムアウトは1000ミリ秒(1秒)
client.parameters.outputs.duplicate = True # みつかった解が複数あってもOK
client.parameters.outputs.num_outputs = 0 # 0: 見つかった解を全て出力
# トークン設定
client.token = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX" # 無料登録して取得したトークンを指定する※トークンは掲載上「XXX... ...XXX」としているが、実際は「Fixstars Amplify」に無料登録して取得したトークンを設定する。
【3】サンプルデータについて
「東北6県の隣接データ」を用意する。
「オンラインデモサイト」では「japanmap」を使っているが、今回は大した量ではないので自分で用意する。
※補足:japanmap
■今回用意するデータの形式:adjacency list
今回用意する「データ形式」は「隣接リスト(adjacency list)」である。
簡単に言うと、「ノード(ラベル)」を並べて、「隣接情報」を表現する形式。
具体的には、先頭に「対象とするノード」、その後ろに「隣接するノード(ラベル)」を並べればよい。
例えば東北6県の「adjacency list」は次のように書ける
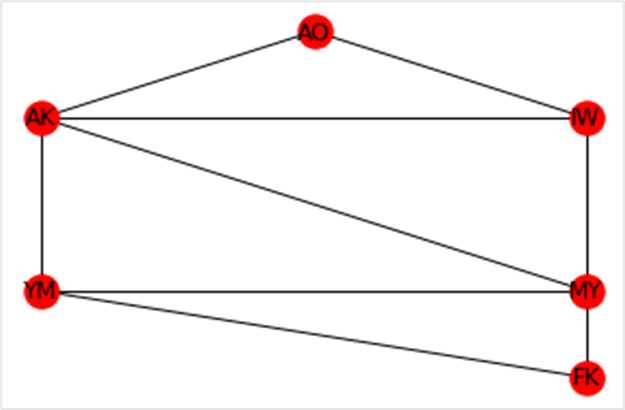
↓ adjacency listとして隣接情報を表現する
AO,IW,AK
IW,AO,AK,MY
AK,AO,IW,YM,MY
YM,AK,MY,FK
MY,IW,AK,YM,FK
FK,YM,MY
今回の「作成データ」は『一旦テキストデータとして書き出して、それを「networkx」で読み込む』こととする。
■「adjacency list」ファイルとして書き出し
text = '''AO,IW,AK
IW,AO,AK,MY
AK,AO,IW,YM,MY
YM,AK,MY,FK
MY,IW,AK,YM,FK
FK,YM,MY'''
with open("tohoku.adj",mode='w') as f:
f.write(text)■中身の確認(※colab上の操作想定)
!cat tohoku.adj【実行結果】
AO,IW,AK
IW,AO,AK,MY
AK,AO,IW,YM,MY
YM,AK,MY,FK
MY,IW,AK,YM,FK
FK,YM,MY
▲「adjacency list」形式のファイルが出来上がっている
■「networkx」で作成データを読み込む
「隣接リスト(adjacency list)形式」のデータは「networkx」の「read_adjlist()」で簡単に読み込むことができる。
※参考:networkx.read_adjlist()
■作成したadjlistファイルを読み込んでデータ確認
import networkx as nx
# adjlistファイルを読み込む
G = nx.read_adjlist('tohoku.adj', delimiter = ',')
# ノードの取り出し(県名ラベル相当)
states = G.nodes
print(states)
# エッジ取得(隣接ペア)
borders = G.edges
print(borders)【ここまでの実行結果例】
NodeView(('AO', 'IW', 'AK', 'MY', 'YM', 'FK'))
EdgeView([('AO', 'IW'), ('AO', 'AK'), ('IW', 'AK'), ('IW', 'MY'), ('AK', 'YM'), ('AK', 'MY'), ('MY', 'YM'), ('MY', 'FK'), ('YM', 'FK')])
■参考:隣接状況の可視化
参考までに読み込んだデータをグラフとしてColab上で表示してみると次のようになる。
%matplotlib inline
import matplotlib.pyplot as plt
#描画用posデータ作成
pos_data = {
'AO':(0.5, 2),
'IW':(1, 1.5),
'AK':(0, 1.5),
'MY':(1, 0.5),
'YM':(0, 0.5),
'FK':(1, 0),
}
nx.draw_networkx(G,pos=pos_data, node_color="r")
plt.show()【実行結果例】

(※pos指定による描画位置調整あり)
【4】変数を用意する(イジング変数/QUBO変数)
用意する変数に対する考え方は次の通り。
(1)各県ごとに、塗りたい色の数だけフラグとなる変数を用意する
→ 例えば4色なら、1つの県で4つのフラグ用変数を用意しておく。
『塗る色を1つ選ぶ=どれか1つだけフラグを「1」にする』
ということ。(One Hot制約)
(2)隣接県で同じ色を塗らない
→ 隣接県同士で1を立てたフラグが、同じ色にあたるフラグなら
ペナルティになる仕掛けを入れる。(隣接制約)
別の表現をすると
「隣接県のフラグ同士で掛け算をして0なら色がかぶってない」
ということ。
※イメージ図(4つのエリアを塗り分ける場合の例)

今回は「QUBO変数」を使用する。
# 4色問題用に4色分の番号を用意
colors = [0, 1, 2, 3]
# 色数と県の数を取得しておく
num_colors = len(colors)
num_region = G.number_of_nodes()
from amplify import BinaryPoly, SymbolGenerator
gen = SymbolGenerator(BinaryPoly)
q = gen.array(G.number_of_nodes(),num_colors)
print(q)
【ここまでの実行結果】
[[ q_0, q_1, q_2, q_3],
[ q_4, q_5, q_6, q_7],
[ q_8, q_9, q_10, q_11],
[q_12, q_13, q_14, q_15],
[q_16, q_17, q_18, q_19],
[q_20, q_21, q_22, q_23]]
▲1つの県に対し4つの変数(選択する色用のフラグ変数)を用意できた
【5-1】制約条件1:One Hot制約
各県に対し割り当てる色は1つだけ。
つまり、各県ごとに用意した4つの変数でOne Hot制約を持たせる

「Fixstars amplify」で「One Hot制約」を持たせる場合には「one_hot()」を使うと楽ができる。
from amplify.constraint import one_hot
reg_constraints = [one_hot(q[i]) for i in range(num_region)]
print(reg_constraints)【実行結果】
[q_0 + q_1 + q_2 + q_3 == 1,
q_4 + q_5 + q_6 + q_7 == 1,
q_8 + q_9 + q_10 + q_11 == 1,
q_12 + q_13 + q_14 + q_15 == 1,
q_16 + q_17 + q_18 + q_19 == 1,
q_20 + q_21 + q_22 + q_23 == 1]
▲「one_hot()」に「変数の配列データ」を渡すと、その配列データの「One hot制約」を作ってくれる。
【5-2】制約条件2:隣接県は同じ色を塗らない
※再掲
(2)隣接県で同じ色を塗らない
→ 隣接県同士で1を立てたフラグが、同じ色にあたるフラグなら
ペナルティになる仕掛けを入れる。(隣接制約)
別の表現をすると
「隣接県のフラグ同士で掛け算をして0なら色がかぶってない」
ということ。
隣接県が同じ色とならないようにするには、隣接県同士の各変数で「AND制約」を仕込めばよい。
■イメージ図:AO(青森県)と隣接する県(IW:岩手、AK:秋田)
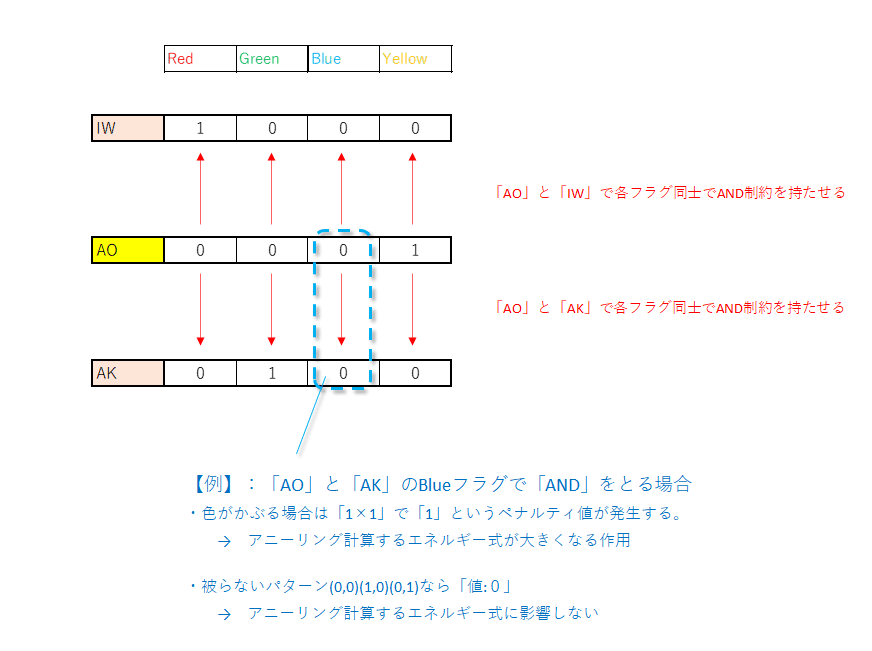
繰り返しになるが「Fixstars Amplify」では制約条件の設定には「ヘルパー関数」を使うのがよい。

今回は「penalty()」を使うが「equal_to()」でも同じ結果を得ることができる。
from amplify.constraint import penalty
#from amplify.constraint import equal_to
# G.nodesでとれるデータをリスト化
states_arr = list(states)
print(states_arr) # ['AO', 'IW', 'AK', 'MY', 'YM', 'FK']
# 制約条件オブジェクトを作成(配列データで複数作成)
adj_constraints = [
# penalty()を使う場合
penalty(q[states_arr.index(state0)][color]*q[states_arr.index(state1)][color], eq=0)
# equal_to()を使う場合
#equal_to(q[states_arr.index(state0)][color]*q[states_arr.index(state1)][color],0)
for state0, state1 in borders
for color in colors
]
print(adj_constraints)【実行結果例】
※print(states_arr)の出力結果
['AO', 'IW', 'AK', 'MY', 'YM', 'FK']
※print(adj_constraints)の出力結果
[q_0 q_4 == 0,
q_1 q_5 == 0,
q_2 q_6 == 0,
… 略 …
q_17 q_21 == 0,
q_18 q_22 == 0,
q_19 q_23 == 0]
ぱっと見、プログラムが何を書いているかよくわからないかもしれないが、以下のようなことを書いている。

ようは「networkx」で読み込んだ「隣接情報(エッジ情報)」を順次取り出して、対応する県同士で、QUBO変数ごとにAND制約式を作っている、ということ。
ここまでで、必要な制約条件オブジェクトができた。
【6】数式(エネルギー式)を完成させる
今回、「目的関数f」に相当するものはない。
【5-1】【5-2】で作成した制約条件をまとめて、その制約条件を満たす変数の組み合わせの中で、できるだけエネルギー式が小さくなるものを計算させる。
# 制約条件をまとめる
# それぞれの制約条件オブジェクト内でも合算してまとめる
constraints = sum(reg_constraints) + sum(adj_constraints)
# 制約条件オブジェクトをBinaryQuadraticModelオブジェクトに変換する
from amplify import BinaryQuadraticModel
model = BinaryQuadraticModel(constraints)▲ 明示的に「制約条件オブジェクト」を「BinaryQuadraticModelオブジェクト」に変換しているが省略して「Solver.solve()」に渡してもOK。(内部で変換してくれる)
【7】Solverオブジェクトを生成して量子アニーリング計算をする
# Solverオブジェクト生成
from amplify import Solver
solver = Solver(client)
# エネルギー式を与えて問題を解かせる
result = solver.solve(model)【8】計算結果を確認する
# 計算結果があるかを確認
if len(result) == 0:
print("no answer")
print(len(result))【ここまでの実行結果例】
192
▲条件を満たすものが192個見つかった。
全てを取り出して確認するのは大変なので、ここでは1つ目の解答を取り出して確認してみる
values = result[0].values
print(values)【ここまでの実行結果】
{0: 0,
1: 1,
2: 0,
3: 0,
… (略) …
21: 0,
22: 0,
23: 1}
from amplify import decode_solution
# qubo変数に計算結果値をセットする
q_values = amplify.decode_solution(q, values, 1)
print(q_values)【実行結果例】
array([
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]
])
答えとしてはこれで取り出せているが、まだよくわからないので「Matplotlib」で描画して確認してみる
【9】Matplotlibで描画してみる
まずは、計算結果から、各県の各フラグについて、何番目のフラグが立っているかを取得する。
import numpy as np
#np.where(q_values > 0.9) #(x行目, y列目)に検出と返ってくる
# (array([0, 1, 2, 3, 4, 5]), array([1, 2, 0, 1, 2, 3]))
color_map = np.where(q_values > 0.9)[1]
print(color_map)【ここまでの実行結果】
array([1, 2, 0, 1, 2, 3])
この計算した色番号に対して、適当に描画用の色を割り当てていく。
今回は色の塗分けとしてカラーマップに「rainbow」を使う。
※カラーマップの詳細は以下参照
my_nx_other_param ={
"node_color":color_map,
"with_labels":True,
"cmap":plt.cm.rainbow
}
nx.draw(G,
pos=pos_data,
**my_nx_other_param)【実行結果】

▲東北6県で隣接県は同じ色にならないように色が選ばれているのがわかる(正解)
なお、しれっと「**my_nx_other_param」いう書き方で、「nx.draw()関数」に渡しているが、これはpythonの可変長キーワード「**kwargs」の仕組みを利用している。
これにより「nx.draw()関数」が受け付けることができる大量の引数の記述を分離してちょっと見やすくしている。
※「可変長の引数」については以下記事の『【2】の「2-3」の「補足」』に少しまとめている
【10】全体コード
最後に全体コードを示しておく。
問題:
東北6県について、隣接した県には同じ色を塗らないようにしつつ、できるだけ少ない色で塗り分けよう。
【実行環境】
・Fixstars Amplify + Google Colab
■事前準備:ライブラリのインストール
! pip install amplify
! pip install --upgrade amplify■ここからが全体コード
import networkx as nx
from amplify import BinaryPoly, SymbolGenerator
from amplify import BinaryQuadraticModel
from amplify import Solver
from amplify import decode_solution
from amplify.constraint import one_hot
from amplify.constraint import penalty
#from amplify.constraint import equal_to
from amplify.client import FixstarsClient
client = FixstarsClient()
client.parameters.timeout = 1000 # タイムアウトは1000ミリ秒(1秒)
client.parameters.outputs.duplicate = True # みつかった解が複数あってもOK
client.parameters.outputs.num_outputs = 0 # 0: 見つかった解を全て出力
# トークン設定
client.token = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX" # 無料登録して取得したトークンを指定する
# サンプルデータ生成
text = '''AO,IW,AK
IW,AO,AK,MY
AK,AO,IW,YM,MY
YM,AK,MY,FK
MY,IW,AK,YM,FK
FK,YM,MY'''
with open("tohoku.adj",mode='w') as f:
f.write(text)
# colab上操作
#!cat tohoku.adj
# networkxでサンプルデータ(adjlist形式)を読み込む
# adjlistファイルを読み込む
G = nx.read_adjlist('tohoku.adj', delimiter = ',')
# ノードの取り出し(県名ラベル相当)
states = G.nodes
print(states)
# エッジ取得(隣接ペア)
borders = G.edges
print(borders)
# 読み込んだデータの試し描画(colab上)
%matplotlib inline
import matplotlib.pyplot as plt
#描画用posデータ作成
pos_data = {
'AO':(0.5, 2),
'IW':(1, 1.5),
'AK':(0, 1.5),
'MY':(1, 0.5),
'YM':(0, 0.5),
'FK':(1, 0),
}
nx.draw_networkx(G,pos=pos_data, node_color="r")
plt.show()
# QUBO変数の生成
# 4色問題用に4色分の番号を用意
colors = [0, 1, 2, 3]
# 色数と県の数を取得しておく
num_colors = len(colors)
num_region = G.number_of_nodes()
gen = SymbolGenerator(BinaryPoly)
q = gen.array(G.number_of_nodes(),num_colors)
print(q)
# 制約条件1:One Hot制約
reg_constraints = [one_hot(q[i]) for i in range(num_region)]
print(reg_constraints)
# 制約条件2:隣接制約
# G.nodesでとれるデータをリスト化
states_arr = list(states)
print(states_arr) # ['AO', 'IW', 'AK', 'MY', 'YM', 'FK']
# 制約条件オブジェクトを作成(配列データで複数作成)
adj_constraints = [
# penalty()を使う場合
penalty(q[states_arr.index(state0)][color]*q[states_arr.index(state1)][color], eq=0)
# equal_to()を使う場合
#equal_to(q[states_arr.index(state0)][color]*q[states_arr.index(state1)][color],0)
for state0, state1 in borders
for color in colors
]
print(adj_constraints)
# 制約条件をまとめて数式(エネルギー式)を完成させる
# それぞれの制約条件オブジェクト内でも合算してまとめる
constraints = sum(reg_constraints) + sum(adj_constraints)
# 制約条件オブジェクトをBinaryQuadraticModelオブジェクトに変換する
# 最終的な数式(エネルギー式)
model = BinaryQuadraticModel(constraints)
# Solverオブジェクト生成して問題を解く
# Solver生成
solver = Solver(client)
# エネルギー式を与えて問題を解く
result = solver.solve(model)
# 計算結果の確認
if len(result) == 0:
print("no answer")
print(len(result))
# 1つ目の解を取り出してみる
values = result[0].values
print(values)
# qubo変数に計算結果値をセットする
q_values = amplify.decode_solution(q, values, 1)
print(q_values)【実行結果例】
array([
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]
])
■Matplotlibで結果を可視化してみる
import numpy as np
#np.where(q_values > 0.9) #(x行目, y列目)に検出と返ってくる
# (array([0, 1, 2, 3, 4, 5]), array([1, 2, 0, 1, 2, 3]))
color_map = np.where(q_values > 0.9)[1]
print(color_map)
my_nx_other_param ={
"node_color":color_map,
"with_labels":True,
"cmap":plt.cm.rainbow
}
nx.draw(G,
pos=pos_data,
**my_nx_other_param)【実行結果例】(※説明上の結果とは別で、改めて実行したもの)
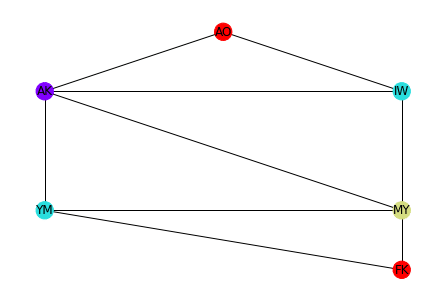
【補足】
今回は「Fixstars Amplify」の量子アニーリング計算を使って、4色問題(グラフの彩色問題)を解いた。
作成したサンプルデータの読み込みには「networkx」を活用した。しかし「networkxパッケージ」自体はグラフ・ネットワーク理論用向けに作られたものであり、「4色問題(グラフの彩色問題)」を解くアルゴリズムも搭載している。
そのため、無理して量子アニーリングで何とかしようとする必要はない。
どちらかといえば
『既存のアルゴリズムの方が優れている、とか、量子アニーリングの方が優れている、といったとらえ方をするのではなく、あくまで「やり方の1つ」として量子アニーリングの場合はこうやって実現することができる』
という感じでとらえておく。そのうえでどんな使い方ができるだろうかと前向きに考えていくほうがよい。
いいなと思ったら応援しよう!

