
QAP.02:イジング変数と「数の2分割問題」【量子コンピュータ/アニーリング@Python/Fixstars Amplify】
【はじめに】
前回は「Fixstars Amplify」を使って、ざっと量子アニーリングのプログラムをやってみた。簡単にまとめると次のような感じになる。
【再掲】
量子アニーリングによるプログラムの挙動をざっくりいうと、
与えられた「数式(+制約条件)」の中で、その「答えをできるだけ小さくする変数の組み合わせ」を見つける。
というもの。
実際にプログラムをするときは
① 目的関数(と制約条件)を考える
② 使用する変数を考える
↓ (定式化できたら、、、)
③ プログラムして実行する
といった流れになる。
引き続き、簡単な例題を使って、量子アニーリングのプログラムをしてみる。今回は「イジング変数」を使ってみる。
【再掲】
「Fixstars Amplify」では組み合わせを見つけるための変数として「イジング変数」と「QUBO変数」を用意している。
・イジング変数:「-1」 または「1」をとる
・QUBO変数:「0」または「1」をとる
【例題】:イジング変数+数の2分割
「数の分割問題」は
与えられた「n個の数」を指定のグループにわける。
その時、各グループの合計値が(なるべく)同じになるようにする。
というもの。
今回は、次の「10個の数字を2つのグループに分ける」場合の組み合わせを考えてみる
■ サンプルデータ
[2, 10, 3, 8, 5, 7, 9, 5, 3, 2]
<解答となる組み合わせの例>
グループ1:(2,3,5,7,10)→ sum:27
グループ2:(2,3,5,8,9)→ sum:27

【考え方】
「数の総和ができるだけ同じになるように2分割する」ということは、
「一方のグループの総和」から「他方のグループの総和」を引いた時に「できるだけ差が0に近づくように分割する」
と考えることもできる。

ということは、各数字の符号「±」について、「プラスマイナスがいい感じになる組み合わせ」を見つけられたら「数の2分割」が達成できることになる。

【実行環境について】
今回も引き続き「Fixstars Amplify (無料枠)」+「Google Colab (無料枠)」でプログラミングしてみる。
【1】ライブラリのインストール(Colab上にインストール)
! pip install amplify
! pip install --upgrade amplify【2】クライアントオブジェクトの生成
from amplify.client import FixstarsClient
client = FixstarsClient()
client.parameters.timeout = 1000 # タイムアウトは1000ミリ秒(1秒)
client.parameters.outputs.duplicate = True # みつかった解が複数あってもOK
client.parameters.outputs.num_outputs = 0 # 0: 見つかった解を全て出力
# トークン設定
client.token = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX" # 無料登録して取得したトークンを指定する※トークンは掲載上「XXX... ...XXX」としているが、実際は「Fixstars Amplify」に無料登録して取得したトークンを設定する。
【3】イジング変数を用意する
QUBO変数と同じく、「SymbolGeneratorオブジェクト」経由で「IsingPolyオブジェクト」を生成することで「イジング変数」を用意することができる。
from amplify import IsingPoly
from amplify import SymbolGenerator
# サンプルデータ
my_sample = [2, 10, 3, 8, 5, 7, 9, 5, 3, 2]
# イジング変数の生成
gen = SymbolGenerator(IsingPoly)
q = gen.array(len(my_sample))
print(q)【ここまでの実行結果】
[s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9]
▲ s_0 ~ s_9 まで10個のイジング変数が生成された
【4】目的関数を作る
数式通り作ると次のような感じになる。
■目的関数を数式通りにプログラムした場合(未完)
# 目的関数
f = my_sample[0]*q[0] + my_sample[1]*q[1] + my_sample[2]*q[2] \
+ my_sample[3]*q[3] + my_sample[4]*q[4] + my_sample[5]*q[5] \
+ my_sample[6]*q[6] + my_sample[7]*q[7] + my_sample[8]*q[8] \
+ my_sample[9]*q[9]
# for文でまとめる場合
#f = sum(my_sample[i]*q[i] for i in range(len(my_sample)))
# アインシュタイン縮約表記の場合
#from amplify import einsum
#f = einsum("i,i",q,my_sample)
print(f)【実行結果】
2 s_0 + 10 s_1 + 3 s_2 + 8 s_3 + 5 s_4 + 7 s_5 + 9 s_6 + 5 s_7 + 3 s_8 + 2 s_9
■目的関数を量子アニーリング計算に合わせる
ここで注意したいのが、量子アニーリングは与えられた数式(+制約条件)の中で、
「その答えをできるだけ小さくする」変数の組み合わせを見つける。
ということ。
そのため、そのままの目的関数(数式)では「全てマイナスをとって最小値」を取ろうとする
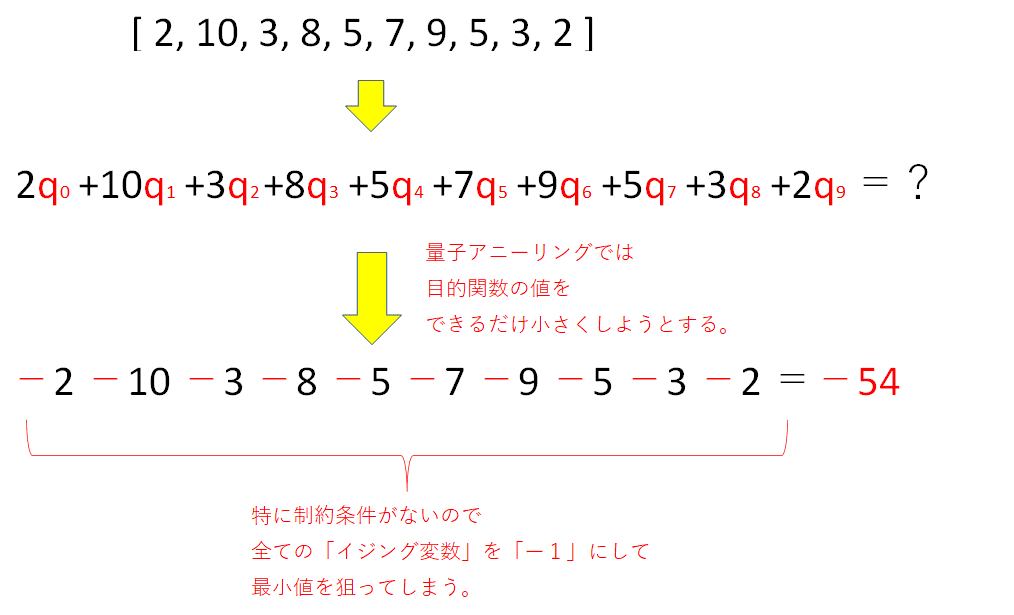
そこで、全体を2乗して0が最小値となるような式にして適切な組み合わせをつくる

■最終的な量子アニーリング計算用の目的関数(完成版)
# 目的関数
f = my_sample[0]*q[0] + my_sample[1]*q[1] + my_sample[2]*q[2] \
+ my_sample[3]*q[3] + my_sample[4]*q[4] + my_sample[5]*q[5] \
+ my_sample[6]*q[6] + my_sample[7]*q[7] + my_sample[8]*q[8] \
+ my_sample[9]*q[9]
# for文でまとめる場合
#f = sum(my_sample[i]*q[i] for i in range(len(my_sample)))
# アインシュタイン縮約表記の場合
#from amplify import einsum
#f = einsum("i,i",q,my_sample)
# 量子アニーリングの計算用に目的関数を2乗する
f = f ** 2
print(f)【ここまでの実行結果】
40 s_0 s_1 + 12 s_0 s_2 + 32 s_0 s_3 + 20 s_0 s_4 + 28 s_0 s_5 + 36 s_0 s_6 + 20 s_0 s_7 + 12 s_0 s_8 + 8 s_0 s_9 + 60 s_1 s_2 + 160 s_1 s_3 + 100 s_1 s_4 + 140 s_1 s_5 + 180 s_1 s_6 + 100 s_1 s_7 + 60 s_1 s_8 + 40 s_1 s_9 + 48 s_2 s_3 + 30 s_2 s_4 + 42 s_2 s_5 + 54 s_2 s_6 + 30 s_2 s_7 + 18 s_2 s_8 + 12 s_2 s_9 + 80 s_3 s_4 + 112 s_3 s_5 + 144 s_3 s_6 + 80 s_3 s_7 + 48 s_3 s_8 + 32 s_3 s_9 + 70 s_4 s_5 + 90 s_4 s_6 + 50 s_4 s_7 + 30 s_4 s_8 + 20 s_4 s_9 + 126 s_5 s_6 + 70 s_5 s_7 + 42 s_5 s_8 + 28 s_5 s_9 + 90 s_6 s_7 + 54 s_6 s_8 + 36 s_6 s_9 + 30 s_7 s_8 + 20 s_7 s_9 + 12 s_8 s_9 + 370
【5】Solverオブジェクトを生成して量子アニーリング計算をする
※再掲:
「Fixstars Amplify」では「Solverオブジェクト(Client設定仕込み済み)」経由で「目的関数」を解かせる。
# Solverオブジェクト生成
from amplify import Solver
solver = Solver(client)
# 目的関数をわたして量子アニーリング計算をする
result = solver.solve(f)【6】計算結果を確認する
答えが求められているかは「len()」で確認する
# 解があるかを確認
if len(result) == 0:
print("no answer")
# 得られた解の数を出力してみる
print(f"{len(result)} answers !")【ここまでの実行結果】
46 answers !
イテレータをまわして求められた解を出力してみる
from amplify import decode_solution
for sol in result:
energy = sol.energy
values = sol.values
res = decode_solution(q, values)
print(f"energy = {energy}, {values} \nResult is {q} = {res}")
print("-----------")【実行結果例】
energy = 0.0, {4: -1, 3: -1, 2: 1, 1: -1, 9: -1, 8: 1, 7: 1, 6: 1, 5: 1, 0: -1}
Result is [s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9] = [-1. -1. 1. -1. -1. 1. 1. 1. 1. -1.]
-----------
energy = 0.0, {4: -1, 3: -1, 2: 1, 1: 1, 9: 1, 8: -1, 7: 1, 6: -1, 5: 1, 0: -1}
Result is [s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9] = [-1. 1. 1. -1. -1. 1. -1. 1. -1. 1.]
-----------
energy = 0.0, {4: -1, 3: 1, 2: -1, 1: -1, 9: 1, 8: 1, 7: 1, 6: 1, 5: -1, 0: -1}
Result is [s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9] = [-1. -1. -1. 1. -1. -1. 1. 1. 1. 1.]
-----------
・・・ 略 ・・・
もう少しわかりやすく、サンプルデータの数字を使って分割結果を出力してみる。
for sol in result:
#energy = sol.energy
values = sol.values
res = decode_solution(q, values)
A0 = []
A1 = []
# enumerateで インデックスと実データを取り出す
for idx, val in enumerate(res):
if val > 0: # イジング変数が1.0となったもの
A1.append(my_sample[idx])
else: # イジング変数が- 1.0となったもの
A0.append(my_sample[idx])
print(f"{A0}:{sum(A0)} - {A1}:{sum(A1)}")[2, 8, 9, 5, 3]:27 - [10, 3, 5, 7, 2]:27
[10, 3, 9, 3, 2]:27 - [2, 8, 5, 7, 5]:27
[2, 3, 5, 9, 5, 3]:27 - [10, 8, 7, 2]:27
[10, 7, 5, 3, 2]:27 - [2, 3, 8, 5, 9]:27
[2, 10, 5, 5, 3, 2]:27 - [3, 8, 7, 9]:27
[8, 5, 9, 3, 2]:27 - [2, 10, 3, 7, 5]:27
・・・(略)・・・
▲各グループの総和が同じになるような組み合わせが求められている。
本来は、「見やすくソートする、1つ目と2つ目のグループが入れ替わっただけの同じ組み合わせを除外する」等のような「後処理」も必要だが省略。
なお、しれっと使った「enumerate」は、pythonの組み込み関数。イテレータでループを回すときに「インデックス と 値」を同時に取り出してくれるものである。
※ enumerate関数について
【7】全体コード
最後にコード全体を示しておく。
【例題】
次の10個の数字を2つのグループに分け、各グループ内の総和ができるだけ同じになるようなの組み合わせを探す
■ サンプルデータ
[2, 10, 3, 8, 5, 7, 9, 5, 3, 2]
【実行環境】
・Fixstars Amplify + Google Colab
■事前準備:ライブラリのインストール
! pip install amplify
! pip install --upgrade amplify■ここからが全体コード
from amplify.client import FixstarsClient
from amplify import IsingPoly
from amplify import SymbolGenerator
from amplify import Solver
from amplify import decode_solution
client = FixstarsClient()
client.parameters.timeout = 1000 # タイムアウトは1000ミリ秒(1秒)
client.parameters.outputs.duplicate = True # みつかった解が複数あってもOK
client.parameters.outputs.num_outputs = 0 # 0: 見つかった解を全て出力
# トークン設定
client.token = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX" # 無料登録して取得したトークンを指定する
# サンプルデータ
my_sample = [2, 10, 3, 8, 5, 7, 9, 5, 3, 2]
# イジング変数の生成
gen = SymbolGenerator(IsingPoly)
q = gen.array(len(my_sample))
print(q) # [s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9]
# 目的関数の作成
#f = my_sample[0]*q[0] + my_sample[1]*q[1] + my_sample[2]*q[2] \
# + my_sample[3]*q[3] + my_sample[4]*q[4] + my_sample[5]*q[5] \
# + my_sample[6]*q[6] + my_sample[7]*q[7] + my_sample[8]*q[8] \
# + my_sample[9]*q[9]
f = sum(my_sample[i]*q[i] for i in range(len(my_sample)))
# アインシュタイン縮約表記版
#from amplify import einsum
#f = einsum("i,i",q,my_sample)
# 2乗して量子アニーリング計算できるようにする
f = f ** 2
# Solverを生成
solver = Solver(client)
# 目的関数を渡して計算させる
result = solver.solve(f)
# 結果を確認
if len(result) == 0:
print("no answer")
print(f"{len(result)} answers !")
# 答えを出力して確認する
#for sol in result:
# energy = sol.energy
# values = sol.values
# res = decode_solution(q, values)
#
# print(f"energy = {energy}, {values} \nResult is {q} = {res}")
# print("-----------")
# サンプルデータを使って分割結果を出力する
for sol in result:
#energy = sol.energy
values = sol.values
res = decode_solution(q, values)
A0 = []
A1 = []
# enumerateで インデックスと実データを取り出す
for idx, val in enumerate(res):
if val > 0: # イジング変数が1.0となったもの
A1.append(my_sample[idx])
else: # イジング変数が- 1.0となったもの
A0.append(my_sample[idx])
print(f"{A0}:{sum(A0)} - {A1}:{sum(A1)}")
【実行結果例】
[2, 8, 9, 5, 3]:27 - [10, 3, 5, 7, 2]:27
[10, 3, 9, 3, 2]:27 - [2, 8, 5, 7, 5]:27
[2, 3, 5, 9, 5, 3]:27 - [10, 8, 7, 2]:27
[10, 7, 5, 3, 2]:27 - [2, 3, 8, 5, 9]:27
[2, 10, 5, 5, 3, 2]:27 - [3, 8, 7, 9]:27
[8, 5, 9, 3, 2]:27 - [2, 10, 3, 7, 5]:27
[2, 10, 7, 5, 3]:27 - [3, 8, 5, 9, 2]:27
[2, 10, 5, 7, 3]:27 - [3, 8, 9, 5, 2]:27
・・・(略)・・・
【おまけ】:energy=0にならない場合の挙動
今回は、2分割したら各グループの総和がちょうど同じになるような都合の良い例(元のサンプルデータの総和が偶数となっている例)を挙げた。
そうではない場合(サンプルデータの総和が奇数の場合)はどうなるかをやってみる。
■サンプルデータ
#my_sample = [2, 10, 3, 8, 5, 7, 9, 5, 3, 2] ※合計54
my_sample = [2, 10, 4, 8, 5, 7, 9, 5, 3, 2] ※合計55:合計奇数のこっちでやる
from amplify.client import FixstarsClient
from amplify import IsingPoly
from amplify import SymbolGenerator
from amplify import Solver
from amplify import decode_solution
client = FixstarsClient()
client.parameters.timeout = 1000 # タイムアウトは1000ミリ秒(1秒)
client.parameters.outputs.duplicate = True # みつかった解が複数あってもOK
client.parameters.outputs.num_outputs = 0 # 0: 見つかった解を全て出力
# トークン設定
client.token = "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX" # 無料登録して取得したトークンを指定する
# サンプルデータ
#my_sample = [2, 10, 3, 8, 5, 7, 9, 5, 3, 2]
my_sample = [2, 10, 4, 8, 5, 7, 9, 5, 3, 2]
# イジング変数の生成
gen = SymbolGenerator(IsingPoly)
q = gen.array(len(my_sample))
print(q) # [s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9]
# 目的関数の作成
f = sum(my_sample[i]*q[i] for i in range(len(my_sample)))
# アインシュタイン縮約表記版
#from amplify import einsum
#f = einsum("i,i",q,my_sample)
# 2乗して量子アニーリング計算できるようにする
f = f ** 2
# Solverを生成
solver = Solver(client)
# 目的関数を渡して計算させる
result = solver.solve(f)
# 結果を確認
if len(result) == 0:
print("no answer")
print(f"{len(result)} answers !") # 例:78 answers !
# 答えを出力して確認する
for sol in result:
energy = sol.energy
values = sol.values
res = decode_solution(q, values)
print(f"energy = {energy}, {values} \nResult is {q} = {res}")
print("-----------")
# サンプルデータを使って分割結果を出力する
for sol in result:
#energy = sol.energy
values = sol.values
res = decode_solution(q, values)
A0 = []
A1 = []
# enumerateで インデックスと実データを取り出す
for idx, val in enumerate(res):
if val > 0: # イジング変数が1.0となったもの
A1.append(my_sample[idx])
else: # イジング変数が- 1.0となったもの
A0.append(my_sample[idx])
print(f"{A0}:{sum(A0)} - {A1}:{sum(A1)}")
【実行結果例】
energy = 1.0, {4: 1, 3: 1, 2: -1, 1: -1, 9: -1, 8: -1, 7: 1, 6: -1, 5: 1, 0: 1}
Result is [s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9] = [ 1. -1. -1. 1. 1. 1. -1. 1. -1. -1.]
-----------
energy = 1.0, {4: 1, 3: 1, 2: -1, 1: 1, 9: -1, 8: 1, 7: -1, 6: -1, 5: -1, 0: 1}
Result is [s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9] = [ 1. 1. -1. 1. 1. -1. -1. -1. 1. -1.]
-----------
energy = 1.0, {4: -1, 3: -1, 2: 1, 1: -1, 9: 1, 8: 1, 7: -1, 6: 1, 5: 1, 0: 1}
Result is [s_0, s_1, s_2, s_3, s_4, s_5, s_6, s_7, s_8, s_9] = [ 1. -1. 1. -1. -1. 1. 1. -1. 1. 1.]
-----------
・・・(略)・・・
[10, 4, 9, 3, 2]:28 - [2, 8, 5, 7, 5]:27
[4, 7, 9, 5, 2]:27 - [2, 10, 8, 5, 3]:28
[10, 8, 5, 5]:28 - [2, 4, 7, 9, 3, 2]:27
[4, 5, 7, 9, 2]:27 - [2, 10, 8, 5, 3]:28
[2, 4, 5, 9, 5, 2]:27 - [10, 8, 7, 3]:28
[10, 4, 9, 5]:28 - [2, 8, 5, 7, 3, 2]:27
[4, 8, 7, 5, 3]:27 - [2, 10, 5, 9, 2]:28
[4, 8, 9, 5, 2]:28 - [2, 10, 5, 7, 3]:27
[4, 5, 7, 9, 3]:28 - [2, 10, 8, 5, 2]:27
▲ 量子アニーリングの計算の性質通り、数式の答えをできるだけ小さくしようして、energy = 1.0となる組み合わせが算出される。
いいなと思ったら応援しよう!

