減衰曲線について(数3・微分積分)
今回の問題はオープンチャットで寄せられた質問です。解答に至るまでの過程が長いんです。
私、ケアレスミスが多い質なので、ミスをしていないか心配ですが、早速問題を見ていきましょう!
今回の問題

f(x)の関数は典型的な「減衰曲線」です。
グラフを書くと分かるのですが、xの増加に伴い(極大と極小が交互に現れる)極値の絶対値が級数的に小さくなっていく、つまり
「振動しながらx軸に近づいていく」
という特徴があるものですね。
先ずは微分!
増減表を書くために微分して1次導関数と2次導関数を求めておきます。
ここで
f'(x)=0とf"(x)=0になるxの値はどのようなものなのかを求めておきましょう。
特にf'(x)=0となるxの値の規則性が分かっていると、その後の解答に役立ちます。

増減表を書き、(1)に答える
(1)に答えていきます。
「極大値の和」を求めよ
とのことですが
f'(x)=0の規則性が分かる+増減表を書く
と
極大値を取るxの値には規則性があること
と
極大値は級数的に小さくなっていく
ことが分かります。
ここで
「極大値の和は無限等比級数の和の式求められる!」
と気付けば解答出来ます。
具体的には

ということになります(ミスがありそうで怖いですが)
では、この後(2)に答えていきましょう。
極値の和を求める、(2)に答える
(1)と同様に今度は
極小値の和を求めていきます。
極小値も等比数列になると予測出来ます。
(1)で求めた極大値の和
と
極小値の和
をたせば「極値の和」になります。
↓のように進めていきました。

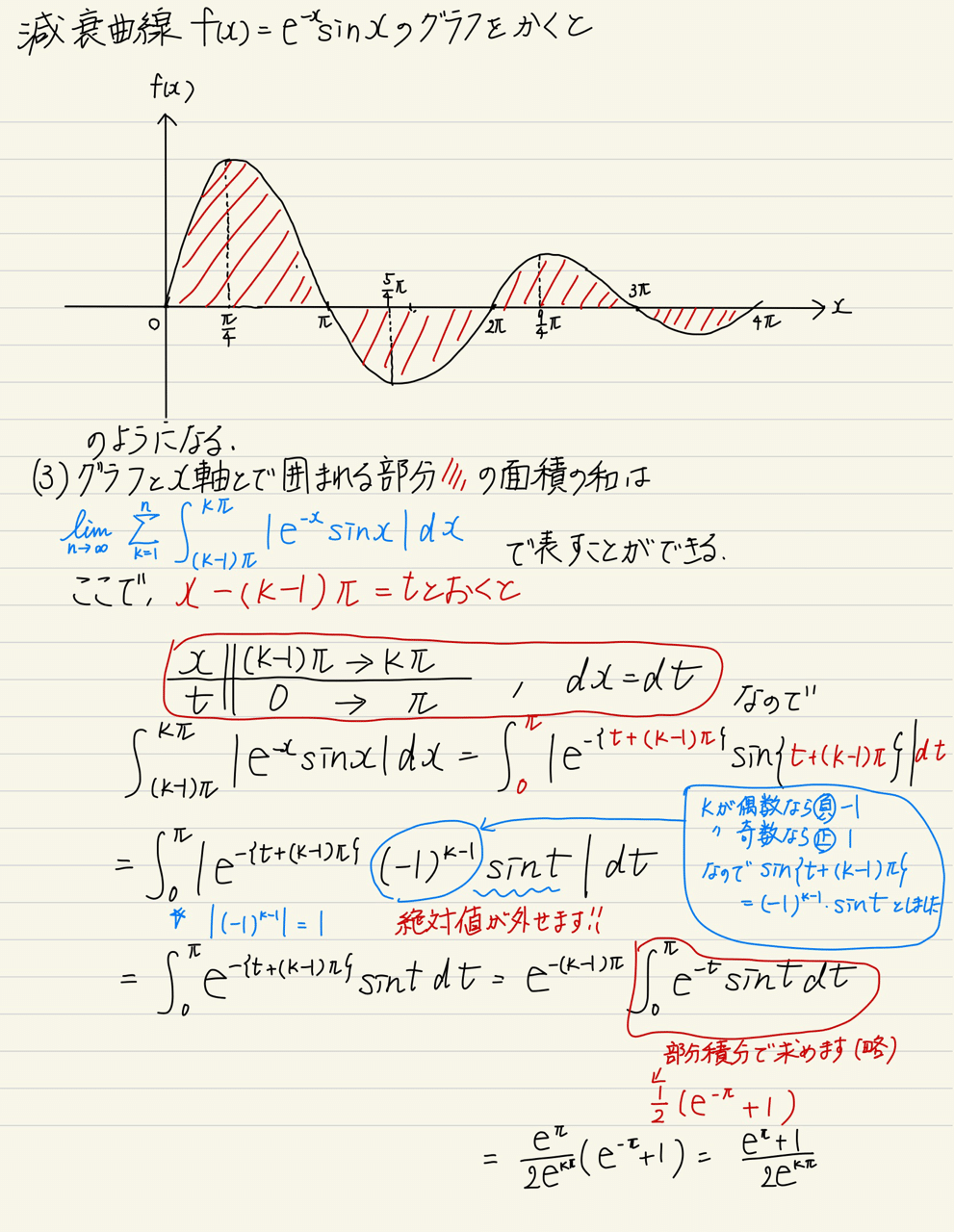
次は(3)
この問題は減衰曲線でよく問われる問題です。
x軸とで囲まれた面積を求める
グラフを書くと分かりますが、囲まれた部分は
0→πはx軸より上
π→2πは下
2π→3πは上
…
と交互になっています。無限に続いていくので、極限limを使います。
面積を求める場合には
区間を0→πにするための置換する。(sinは0→πなら0以上なので計算しやすくなりますね。)
そして
x軸より上ならf(x)のまま定積分
下なら-f(x)にして定積分
なので、絶対値を付ける必要があります。
この絶対値を外すために(-1)のk-1乗をかける
ということがポイントではないかと思います。
ついでに(4)の回転体の体積も求めてしまいます。


長かったですね。
(3)減衰曲線とx軸とで囲まれた面積
は
区間を0→πにする置換
絶対値を用いて表す
→-1の乗数をかけて上手く絶対値を外す
ことがポイントです。
(4)回転体の体積は
輪切りにしたときの円の面積を定積分する
ことを意識しさえすればOK
計算が煩雑なので丁寧にやってみてください。
それでは最後まで読んでいただき、ありがとうございました&お疲れ様でした。
