白ましゅ格子配置に関する考察
先日semiexpさんのリアルタイムソルバーを利用して、白ましゅが格子状に並んでいるときの挙動について考察が進んだので記事にまとめます。
なお、厳密化に複数箇所で失敗しています。正確に言うと手筋の適用可能範囲の考察が不十分です。下記の考え方を踏まえ、個別ケースに関しては適切な考察を踏まえた運用をお願いいたします。
格子配置とは
ある穴のない領域を市松状に塗り分けたとき、ある色に塗られた全てのマスに白ましゅが置かれているときに格子配置と呼ぶこととします。また、格子配置の幅を、その注目している領域の縦または横のうちの短い方と定義します。

これは幅5の領域。
「壁」と「方向」
「壁」を、格子配置内に引かれる線分一本一本とします。
この時、多くの場合壁はおなじ領域内で同一方向(時計回り/反時計回り)に連続して曲がることがないことがわかります
「多くの場合」というのは、格子配置のサイズが小さいとき/注目している壁が端であるときに例外がある、という主張です。
下図のように緑線が同じ方向に2回曲がった時に、U字状の線が内側に進んで破綻する/外側に進んで破綻するため、一部のコーナーケースを除き成り立ちます。(一部のコーナーケースとは、下記の破綻図に使われている白ましゅが欠けているような地点で壁が同じ方向に2回曲がるケースなどです。同値性未証明。)
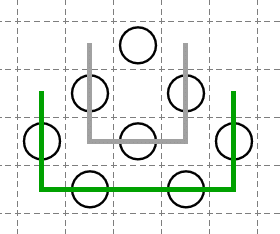
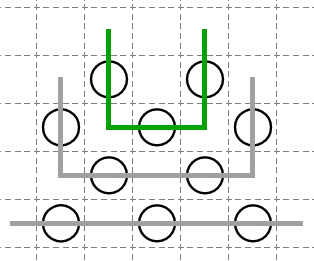
U字に線が曲がらないことを仮定すると、壁は左上~右下に伸びる、または、右上~左下に伸びることになります。このことを「壁の方向」と呼ぶことにします。
壁の到達範囲
壁が伸びていく時にどの範囲まで伸びていくのか、というのはこの後の議論で非常に重要です。
格子配置の中では白ましゅを3回連続して同一方向に通過出来ないことを踏まえると、壁の到達可能範囲は縦に2回/横に1回の移動を貪欲に繰り返し到達する地点から、横に2回/縦に1回の移動を貪欲に繰り返し到達する地点までであることがわかります。
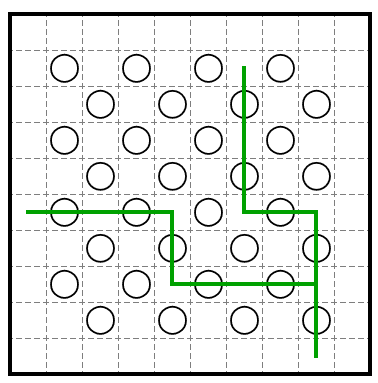
壁のアース
この壁が、盤面の端のマスまで伸びるとき、「壁がアースしている」と呼ぶことにします。
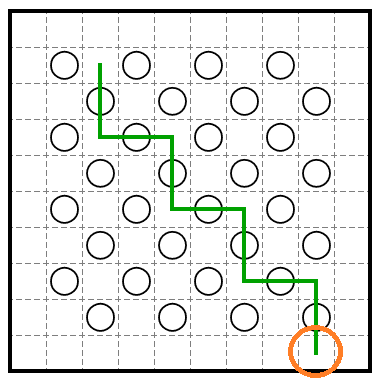
壁がオレンジ丸の地点でアースしている
壁が盤面を分断する事とは、壁の両端がアースしている、と言い換えることができます。
壁の本数
壁の向きが決まっているとき、それに直交する方向の対角線上に並ぶ白ましゅは必ず異なる壁が通過します。このことから、領域内の壁の本数を評価する事が出来ます。
理論適用の具体例
つぎのような盤面で線を一本仮定しました。この時点で破綻している事を示します。
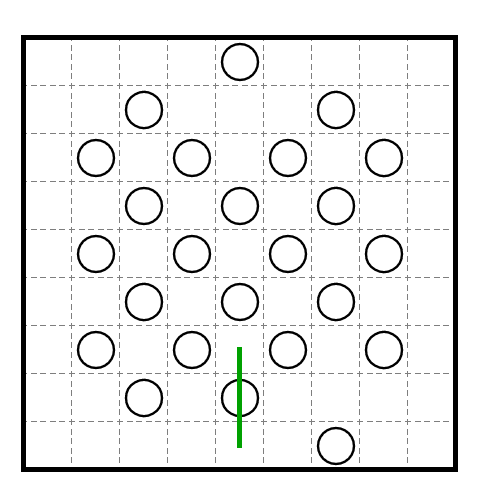
問題引用元:SP1氏twitter
まず、この線が格子配置の領域内でU字に曲がる事が出来ない事を確かめます。
次に、この線が格子配置内でどの範囲まで伸びるのかを検討します。すると、貪欲に進めたこの時が最も遠くまで到達していることが分かります。
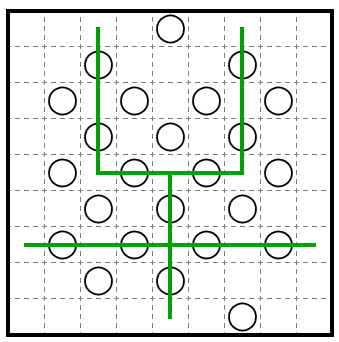
最後に、この時にこの壁の両端がアースすることを示します。
上図の範囲内で格子配置外にこの壁がのびる時の事を考えると、パリティより下に示した8本の線のうちのいずれかを通ることが言えます。
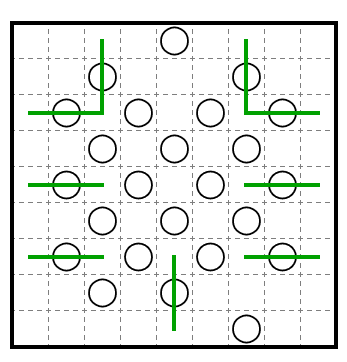
この時この壁は両端がアースしており、かつ壁の両側に白ましゅがあるため盤面を分断する事になります。したがって破綻が示せ、最初に仮定した線が間違っていた事が分かりました。
終わりに
速報として文章化することを優先した結果後半が厳密性の欠片も無い主張ばかりになってしまいました。申し訳ありません。
本手筋に関連しtwitter上での議論に参加していただいた皆様に感謝します。