高校物理の学び直しVol. 019 【円運動の問題を解く2】

今日は以下の問題を解きました。
問題文

長さℓの糸の先に質量mの小さなおもりが付いている。糸の固定点Oからℓ/2だけ下には釘Pが打ってある。重力加速度の大きさをgとする。
（1）図1のように糸が水平になるまでおもりを手で持ち上げ静かに手放した。
（a）おもりが最下点Aに達した瞬間の速さを求めよ。
（b）その後、糸が釘Pに引っかかりながら回転した。糸がたるみだす位置は最下点Aから測っていくらの高さにあるか。
（2）図2のように初速v0を与えたときに、糸が釘Pに引っかかりながら糸がたるまず1回転できるためにはv0はいくら以上でなければならないか。

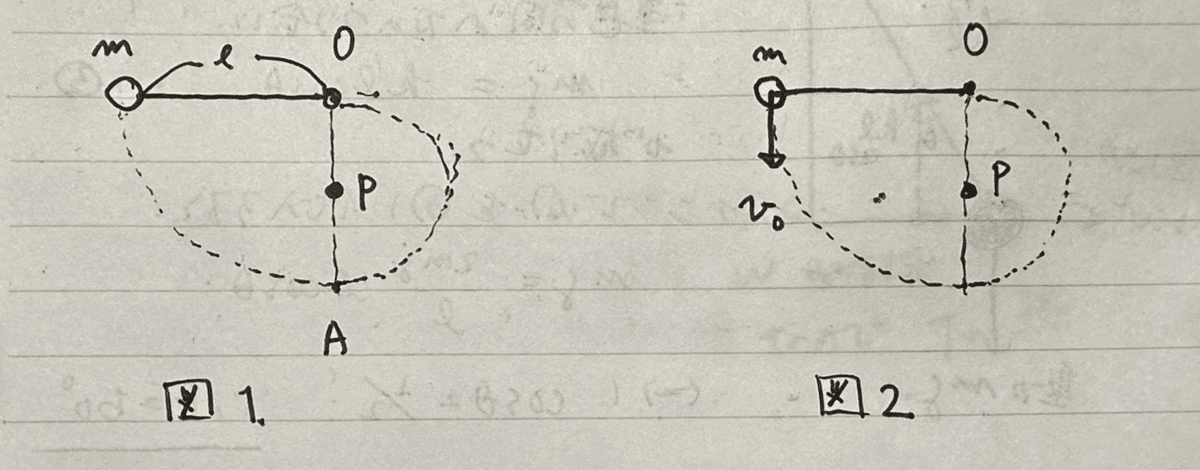
（1）の（a）はエネルギー保存の法則を使うとすぐに解けます。(b)はエネルギー保存の法則も使いますし、円運動している最中の小球に働く力の釣り合いを考える必要があります。また、その時の小球の位置をθなどを使って三角関数で表す必要があります。計算もやや複雑で、計算力も必要な問題です。そして何より『糸がたるみだす』という言葉を物理的にどのように表すことができるのか？も問われます。
（2）も（1）の（b）と同じ考察力で解けます。計算は（2）の方が単純です。
解答を手書きのノートの写真としてアップします。

物理はやっぱり楽しいですね。