
Factorioグリッド初心者メモ:(5)ハブグリッド
Factorioのグリッド型は、あるグリッドで作った素材を他のグリッドに列車で輸送して使うことができるので、グリッドの位置関係をある程度無視して拡張できるメリットがあります。
しかし無計画にグリッドを拡張していくと、不足している素材や余っている素材がわからなくなりがちで、ボトルネックがわかりにくくなるデメリットもあります。
このデメリットを解消するための1つの方法として、ハブグリッド(ブローカーグリッド)を紹介します。
ハブグリッドとは
あるグリッドで作った素材を必要としている他のグリッドに直接輸送するのではなく、あるグリッドで作った素材を一度ハブグリッドに輸送して、その素材を必要としているグリッドはハブグリッドから輸送する形にします。
各素材は余計なハブグリッドを仲介して輸送されることになりますが、ハブグリッドに素材が集約されることになり、全体の見通しがよくなります。

ハブグリッドのメリット
生産グリッドは生産に注力でき、疎結合化が進み、よりスケーラブルに↑
各素材の過不足状況をハブグリッドの状況を見ることで把握可能に↑ハブグリッドのデメリット
生産グリッド以外の余計なグリッドも作ることになる↓
ハブグリッド周辺の交通が混みやすい↓
参考(導入の背景)
非同期メッセージ処理の1つであるpub-subモデルを適用しています。
(Factorioを遊んでいる人はApache Kafkaを利用したことがある人も多いと思います)
グリッドの形
搬入側は左下から右斜め上に向かって入って左下に出て、
搬出側は右上から左斜め下に向かって入って右上に出る形にしています。
BluePrint
0eNq9nd1y3EiOhd9F13IHMxP5g36VDceE7db2KtYteWW5dyc6/O5bJauqqFKieA6SrJuZ6R77qySSSYLAAfDPzeevP+6+Pd0/PN/8/s/N/ZfHh+83v//HPzff7/98+PR1/++e//3t7ub3m/vnu79ubm8ePv21/6enT/dfb37e3tw//HH3fze/h58fb2/uHp7vn+/vfv39l3/4978efvz1+e5p9weOf/PLj6e/7/748AK4vfn2+H33dx4f9j+044jc3vx796eL7Nh/3D/dffn1f+aft++Q8c1iPrwu+D2y/JZfodNv+S1WOtj0Fvvlvz7dP9hwfQPv4AS78Bz7F95bYcaQQSbcmAUzZpDIWbMy1gySl8zZ0GtvuD2VvDfLW2TpIMNEbvsZM/WYpzP0/fnubm/Mu+/P75l6MmLuGzFE9g5CLjmxW4Ncs8yuecf787+erd0Jr1R9S609aqapFVhrQak596m9gxkqTT2zQOhRG0oNqRKGVR4LWDZOMDYH3LQx8FjAthE8Xan8Ytb4lhl7TPBwpdZndtcJn62k/avv7hX4dsqnlfYo+Fkybs/uhldsbWXqW7F3y0f0jZQisd2KQgXf74SfopTxDU/EKUr4XiX0HZXl0o2U0LdSLvieJ/jklFdD1rS86Ql+K5VKUOGTVJSgwm+lGggq/FaqiaDCL6VK7JbAp6kSuyXwYarEbklEqY3YLUkwldgtgc9WY3YLPluN2S34bDVmt+CzpcxuwWdLmd2Cz5YSu5Xhs6XEbmX4bCmxWxk+W2EitisnHEvsVxYcy2xYxrHMjhUcy2wZfMBCYLYM/6YKzJbh31SB2LKCe4OB2LKCe4OB2LKCn7JIbFnBT1kktqzgpywyW4afsshsWWFidOkYAKxyHgDshYVKxSKLJZHc02n7fP/nh7uvuz/8dP/lw7fHr3cXPOZ9zOnhbme6z48/nvaR6p3XG0U+9n5BmV9Q+xfabZ16P1An5gdOt0r3GnLs/kSg4q+xcZtQwRh8yEqCEwae3Y31nNu716twcZQ2ASFuMuJxzux9/VbqTM7ODmYF8EyGyJqXCCsenqe199le2QAIslFtIkMKyE417oTNDgJk0UYGE8+X3IvYtMSFwc6ZvQPb+JCIAlfPh0QQKh8SQah8SASh8iERhMqHRACq8iERhMqHRBAqHxJBqHxIBKHyIRGEyodEECofEkGofEgEofIhEYTKh0QAapj4mAiE5YMiENYRFYG4jrAIxHXERSCuIzACcR2REYjrCI1AXEdsBOI6giMINziiIxDXER6BuGi2LAru04WQ+KgLtFrhwy4QN/NxF4hb+MALxK1k7hjx7kNwfIRpVyYUlEyeQncVruY46A5aAhQtuJrjIBk4x3YVLaia48XsL1QBdj7yJwtbraBf9tPhO7S90/H1zZvpu6qFvvis0DoE7AaotBABs2lj1WLn2K6uK5Kyw1aAteIaj+Nakc1PgZMznq+1ewZSZJVt52vtmyDR2AQ8VRN6sqZjzKwlJMITcN3H0SfADFHYJ1dBboXKrxayL//W2nG7JKUickns/ZKuJHWiRY7QAwHXfpy4yOEVVu0LPWmElftCzwRc/XGUZEJnAdd/nLjIXSuFfIi37i0rlXy+NmTfQWViNba967wJHTlsyDMw06FDDEvHDjEsHTzEsHT0EMPS4UMMS8cPMSwdQMSwdAQRw9IhRAxLxxAhbKFjiBiWjiFiWD6GiHH5GCLG5WOIGJePIWJcPoaIcfkYIsZFlfZB+m/JPlXpyCS02spHEFsFPJkaeG4GPJkaef+7X1xWE+tv9p0iVKtx8jARr6jSKeWGFD6Rgo1jiV6rUPQFVmzMvj4hfUEgJBuHCDpmED4y35Aiuzbx92lXYhIaGNQor48TjUhdXeScbkUipi3RTjcSfsY1G7Uy2Ew73RC20E43hK200w1hG+10Q1ilnW4Eiys3GrNluHRDmS3DtRvKbBku3lBmy3D1hlJblmmnG8IW3umGuJV3uiFu451uiKu80w1w44RqEMPUf+v0qYF35aHVRto51gDUzBIyjmDcDf06ceGdg27qM86EG0gbkGOPEQ1IDDlOYL+NU3+RF3AXVVmHVhOyRc3n0L43QLf2fFLaoX1P7t6zjHQjEAZhpBuhfxa69yws3QivSXZFeuMQ0o3DZ6J207Ux8GfKImWuGUwkD1WAm9jkxVOFt92QfLyJuiD4BZXDZZCSnysFaVUxkZ8rsvy5EnElRs39A9g92DGynysYNrGfKxhW2M8VDJvZzxUMW9jPFQxb2c8VDNvYzxUMq+znCoTFNRnKbBned0OZLcNVGcpsGa7KUGbLktCfKxg3058rGBfVZEyl/xTvUyv9EYStttGfFQpkzWNS3jnpvxSFjwZaJNy9k8svarzbxkve/xIp0U5I35uZySqAStNDPF1zp5S1Rf3Y/YlM+znGWp2R9H3bO6TpFf+5BKRlojT+eyZD3zOi7PdBA74PsuPg9PcrOw6OQYpUPfRBU/P+Nt15q01L9zYl+mocD6exWqEPZ+2D+JNjgAr1hRCnCTgvuHCipMurI+VI57dx91Mj03Kk89PcPXOFliNhWFqOhGFpORKGpeVIGJaWI2FYWo6EYWk5Eoal5UgYlpYjYVhajgRhKy1HwrC0HAnD8nIkjJu4jMC7x3afKnzkHunEWvkyEON9UAvvNxikyr/TDVKj3+n99AGufji+0/sgXO5wfP0aoED6vXFCMjktOr11hbz1lni3WiG3ujnC2oZlM38jG6TC38gGiQ1f73e7C2LD1yZISedUgNtD2dNhrU4D5ZzGKQLOKa5TqLl/5Pq9gRPpnIJYIZ1TEJtJ5xTEFtI5BbGVdE5BbCOdUxCrpHMKYRPRaiIw2EA6pyA2ks4piE2kcwpihXROQWxmnVOQW9g4OMilI9Ygt7HOtCBUWiP+brX9zul0EM54f6VAB+FMEh29NkmJ9kFSHyS0D2KAMu0uGKBCO9NAlWIK1eVM71aJONMp0DHqDrl7QJi5H5ctS4z6kMubTUz3ON7IBinSN3LugxJ9IxsgoW9kA5RJr7wBA7RiGYN2b150dsfRQweqWRMuJKi5f467xwEXEtRKYHEhwdFDh7CB9tAhbKQ9dAibaA8dwgrtoUPYTHvoELbQHjqErbSHDmEb7aFDWKU9dASLSwqU2TJCXzAxe0aoDSZm0yTxHjrEFa7n1bu3Q3dYkGTeAem/EaXwDohBqrwDYpAa7YDUPkhpB6QPynzgzQAFp8sL1U0mvFPD0VEHihtTpoaE1mSvuj8I6nRG9ovekZ8fv13wSc4SN7s7+Pvzp1//++am+wOn4/L18c/778/3X35Nk/zw7dP37/d/33349vT49/0fuz/8/kV1+jgoffF0mgkReHxaxs8P1qcv//3h/uH73dPzAq1Cw1/fNHRYYEeWrQNmkUWzzEQLPD4v4wNuGSEt80bBsMDOLDsNmKUum0UG8GUZn3HLFNYyBWdXll0HzKLLZiGOqbJLPx3Tv+7+uP/x15ISrbWzX3gjRku7j7Ec28fuFL2BI7svXVmw0kwJweOnZTx+ameLxTahJpw9seyBI6vLr6c68HLV5ZdrxU+tsm+oir9ZlX2zzrQVvFmW336VPbWaL57a3VMg7T5Hs6TuyX2jy1iwFPs2bCPHdvmNNZNs8PjlN1YjTi77Vnkj2lhgs2/DNnJsl99YbcAn1raMJ04u+0Js+MtWG8se8InDtPwK1GmEv/wOVNwrni8XM45GAs6+BTWNWGb5NahCLJ59mcxUJdjTfp7TMpw0meptzv3HvZYRYy1/XGkd4S+/HbURm8G+r97IUJbg5OebTEMHePFtKFMY4ZdlPnOGK2ucRMALC5cRy7Rly2Ri8Y1dPFVFFiblQnQyE7CgD6C3PsL5A2jva07dh49MjQ9u177JlQ9u90mEdOUY3DZIgQ5uax8U6eC2AUp0cNsACZcID0CHOQloyr68QoEOc4ILWmrox8n70+wrOb0OxPJpewjLp+0RbOTT9hCWT9tDWD5tD2H5tD2E5dP2EJZP20NYPm0PYfm0PYTl0/YQlk/bI9jEp+0hrCNtD3EdaXuI60jbQ1xh++GB3My2mAC5he3WBXIrLwWGuHQbXpBLt9rAuIL2MYyx74akLjXwnm7f9WKacFz2BiXxnq5BYjsGxBD6ILZjgAkqrKcbgFZ5IpXGGutrrHwjhGW1kKAtNQ5a0iDARc8kMf/7+PjH3cOvj+WeT/rbcXtfPgQ/f3oyfP2ZOsb+OJ7xJujbeCaKuUAtZ6tceiLMNTGPnx+/PT51rr1Nxy+dLkPW0KUEo6mfDMle0jK+OLQjL3vWpXlULjatraE9sS9d19CemPgyObQnpi0YJUtepsU19CX2pac19CU2XhwaENsWHrWKTStraEjsS68ODYm92LaGlMNerK4h5TDxdXJIOUxb1OAQb9i0uIaewr70tIYaxMaLQ1Jh2yI7xB82rawhybAvvTo0EvZi2xqqCHuxuoYqwsQzepHl52wLDh2ETYtrSBPsS09rCCtsvDjUCbYtskNHYdPKKuoD+9rrKuoJm9886gbbHOrRM5i4MW3H8qOb0nYsP7s1rpLjt5ebVtEo2HzxaAhsc2SPasDGlVV0AvbV11V0Aja/eXQCtjnUowywcHlMhbH4jshT8GgB7OVGIBYRQrwUjMhzccWPz4eKGrPv6q/Q05uk/l4l0OL0sUtH6+Bi6QehYpeKh9Nj7kf0QpeLh9Oj9iNxqcutdMC3HyrMhEhCwmWS0gFfg4SLJOS0GV1QoAO+BggcNlIOcTpgiETm9RLW6gQ6cbXM7tw3By6H3YFL0j1wwQz+Pd39z4/dfy9E1uJLFPT1z/7rP++/7v7C/jf/ubl/+ONufzecoqpPjw8fvn399LzXAX15/PHw/OLQTNPP/sqKJ9KXjGdfYJVJs1hkei9M2m+KUb6SQ/OYVK5hUvWsLF9hZXHyBB+tzY6eojybFj1Wq9ewWvKsrFxjZa4AqrkDrgCqSSseq7VrWI2Ivbbl62zsI08vPfL2tT/7x2iWdFta/20SPQ+YWeh0O9OmybOy6RorC54gs7XpKXqCzCbN84DRa3gHSTwri9dYmSsYbe5A8QTKTVr1WO0aDkDyOE16Dacp4TEDXXZNxFMhadOCx2rXcE0keiL75nUmtoy1XHyV/So+39c13RbN/QtwPWCu4SWI55NtFpbfcGXFkyYwN716UhgmzfOAmYfvNzSbupZ2DeckT67chLUJ2VUXauOiy3DX8AJyoiuh0sVH1q+q+9sa+oHTzKQhlt2OnF2Wvcb7OBfX0q7hxBDitPmCzE1wlafaON9j5hreQplcS7tGJKMEV8rI2oTiKny1cclluGs4A0VcS7uGB1WYJOuyo0J0jJpfn4mrgBA5hPMH2kIxY55J8S4rsUM4P1emFDvPBHiX1rp8LipcOdGOOZguh6+VMNIula+VsEh8rYRF4mslDHPztRIGiK+VMECVrV4NgP4+47OrDtWrGFbZ6lUIi8+1aoHBBrZ6FcNGtnoVwya2ehXDClu9imEzW72KYQtbvYphK1u9imEbW72KYZWtXoWw+HysY/Uqxg109SrGjXT1KsZNdPUqxhW6ehXjZrp6FeMWunoV41a6ehXjNrp6FeMSVbHEvhV8claIgeE6fL2u81Emh69nkBy+nkHifb3aB/G+ngHifT0DVLkOMHFart8sM6kbUGnZ+gvTMTVU3eqTtYTJo4YqSOVrCVS3+ZkwqiAfniXEMdXRhkZNY0qtDVcmHgUTuN3Zo7UC2WVMkbShReuYimvDlTWPugncD/XosDB2nMZ0VNtZlNH/Nfaq45jEacOrTmMSpw1XJh5RErgf2SOfAtllTP60oUXrmPxpw5U1j/wJ3A/1iKEwtk8geA0vJYUxadSGK4seMRO4H8kjuwLZMiab2tCi2SObAq+6jOmGNrzqOqa12nBlzaNoAvdDPfomjC3ToKRoO5O6NItzNdCGS4sueRK4JcklpQLhMqiE2tCo2aVMAq+7DOqUNrzuOqhT2nBpzaVTArdEXaolDJ6nQQ3TdkbNYVDDtOHSfKIjcEtc3fZRuAzqmzY0ah7UN224tOLSN4FbUl1qJxDeqBYF/Sj+TOh4aVDoKTl2Nik0Lk0KLTO9IjJHITQyZD4THWLjgM8zJLlLjXy+rJ/AKYnPlxkk4fNlBinT+TLtgwqdLzNAfMNXA9R8g3WDIj1KS1FqsG5QcrBuGRnoOMtmtb52sIwMdJxls0x89DQwVeh5Rwx0bIllyyrNTU2z5FWam5r44smAgZapngwYyG6rdCY1zaKr9FW18ERDvhkNswzRnm9mCJAdV2mKapoleZqigksX92Dd119425kktn1N422TbneSMjTQcVq2VFml4auJr55MErgRzZNJAtm6SrdWyywjPf90+QVLtPxT9g1ITHNU9g040vtPl9+AROs/ZV9R9ChHzRefCr+aduzLB29b6Q5UKyO9AnX51TLSKlCXX4xEp0Bl31xE20Al31x1pIegLr656sggx1nWwcRHTw4DtEzy5F5AtqzTgta0S16nBa3JL65MBWic6spUgPC2Tnta0zLqak+LLX6mwqQH7HYfy78aUNzWGG5b7fZUqiGs08DWMlhYqQGvyU+uZAO4Ib7uuyA8r9Pc1rTMSs15TX51ReZB4/g684JwXaexrmWZOLli2NjiZ+pDegjuy4rPHhIvPlu/X26dqRG5gb5YaLDiAypPIWPtm1z4kLFBynzI2CAVNmQcQx9U2ZCxBYJLe7JeBikbezZAaeIG68a4nN+o+PzIerLX8t2Kj4+sicEmtjQZwwpbmoxhM1uajGELW5qMYStbmoxhG1uajGGVLU2GsDKxpckYNrClyRg2sqXJGDaxpckYVtjSZAyb2dJkDFvo0mSMW+nSZIzb6NJkjKt0aTLEzRNdmoxxA12ajHEjXZqMcRNdmoxxhS5NxriZHKx77oakLpWf32B4SZmf2GCR+IkNFomf2GCQCj2xIaY+iJ7YYIEi7ScbIHpKQ8zLY28rLms5Yo31ZXbWb0zLUqA607hAs35jQS66UnN5Y4Q+p+G+VTNyuty2qkJtq06zfl95Sw+pmcxluQI9Sne/19GyRKPNVh2ZGnkSoNh4j5zl5T7o0sQhvLFpq+hV7Esva6htbHx1yGFsWzSHAMamraJJMS+9TWsoamx8cEheTFu06BC52LS0hqzFvnRxyFrsxeY1pB/2YssawhUbXx3qD9sWzaFTsWmrqEfMS19HPWLjg0PhYdqC0YssvxTWUYjYl+5RiNiLzWsINOzFljUEGja+OgQati2aQ5Jh03QNEYZ16W1I49GW8cEhwrBs0RhJhy7T0ipCC/vaZRWhhc3PHqGFbY7ikVbYuLqKmMK++uYRU9jL1VWkDOZyw7SKlMHmB4+UwTRHiB7xgo1Lq8gV7KuXVeQKNj97FAW2OYpH/WDj6iqSBPvqm0eSYC9XmUK6fjCizWUSyKzf+H706O75vxdEhCDlY/cnAjnw9zwSFbvUSA/8PQ/rhS438QHjtByIboQ4Il6MZzZCHJHSZVLhA9EGqfKBaIPU6EB0/3jM5BGf7/9cEuhIm90jb+7vKHIbZOqOkGppoqPd/dWmwM0njg24lxMfQjdW5wmhd0HcoOPYncrbUt09bXLt78jYtOMoW5Vst+SZdhyz8fRP/mnHL8wzu+53xqgnaq7BfbOg4oYm1aHunhuujBgCOFuPtdkSPMFckzY27XhLq41NO95yZeIJ+po7kD0BaZM2Nu14S6t5ph3b1+mfdtx75O2LpfaP0bZ7Z+0+7GP/CsbGHW9o2zw27njLlXnGHZu7nj3jjm3a2LjjLa02Nu54y5VlT3Tf3IHiie6btDrUOXNLq7WhbqNbrkw9KQtrB8rk6OJp08bGHW9oteIZd2xfp3/ccfdd9qsdwL7CbPcui6l/BTLUHXRL2+ah7qBbrqx4Ei/mrldP4sWktbEOoFuaTcc6gG64tOqad2xuQnXNO7Zxg/OOtzRc8nT5tK9U/OOTe4/A174Hu8df6ocx6uDA4y1NOzjweMulVVcGy9x1V19SG6djHTk3NFwb7GO65dJcA4/NTWiu3qM2bnDg8ZaGGxx4vOXSsiu5aG6Cq7+ojSMHHr8aaqHItM00eNBsYnt9yk9Ofl2jKUFvyg48jt1mp40YOhkv53Hmyrq/Pn39uvjKTefO4tukgcqttv7bVvmycmvRwi66Xl50vG3aT1UT4yflcj5vprQDso9BxEw/5v1y9ynI0P+qU0fq1Vgzn3qtfZDSWdEuSPGxkscEpgEKdALTAEW6ULwuqxkUnyl5LBSHsEIXikPYTBeKQ9hCF4pD2EoXikPYRheKQ1ilC8URbJjoQnEIG+hCcQgb6UJxCJvoQnEIK3ShOITNfKE4xC18oTjErXyhOMRtfKE4xFW+UBzhxokvFIe4gS8Uh7iRLxSHuIkvFIe4Qs+wxriZnmGNcR0l6H3nIzpK0A2SowTdIDlK0PukxJegax/El6AbIF4/Z4ASNw07xeWqaZ1p6ZZrkdPUX9igWk63imeoTy3XkHpznWnnqGnY7/Gli29jqrQNjapjSr7tVsbo5TK53Yx6Tlh2HFOsbWjRNKby23Bl4lG/gfuRPTo9kD2os9vQoi6dHXjVbUwBt+FV65gCbruV5cmjWcP2w6euA9lxTIO2oUUHdXsbrkw8ejZwP1zKO5BdxpRzG1q0jinnNlxZ82jdwP1wqfIwdpnGVHXbWbQEj6oOvOo4pirb8KrTmBJvw5WJR6EG7kf2aOlAdhnUwm1o0jqohdtwac2lhQO3RF3KOAxep0Gd3HZGpRSBrEfg1Ade47Vd06CIbcOliUt1Bm5JdinkQHgZVJFtaNQ6qL3bcGmuyRXolqhLPYfBnarBa7gGLQyK3zZcWnSJ38AtSS4pHAgXpomHEcWfaf+gadhRyWnYOpcDQhqscH5HvhE1aWtmvxBt1Tl5GwzPzxv3QdcS86Vr2evJdvbpX4qSQ77PEz+9zr6qE59Q7OelCGWhXE6VaeTTgAYpsWnAFPogYdOAFiizaUALVHxDvlNAmhPrTAmIDPlOgRzyrdrWaC2815T2zaNrNEa28PvXh6PZ8HvbSx8eHPlKGB7XaGx8wTJpjc7GF/jiyMDBxsmO1CEML2t0Jr5gmbpGY+UL/ObItcHGUUeyDYWPdPo7NX6wLUN0+pvh0MVH98Tv159462NIeynr3TlNNXzs/2Jao3fyBXPJGq2fL/CzI2UGb0dx5MxgeF2jdfMFy7Q1ejdf4KsjyYQahxjDqPQ7N4Y1WjvblonRkZKBF5/c47+7j4jXLjYv9a+750T/i2T3s7JGh+kLNstrtJi+wC+OrtDwnngaWMPwtkYH6guW0TVaUNv8NDlSQ6hxkqfBNQyPq3SovmCatEqL6gs/IJ5EDWwfVwdsmF5W6WB9wTjV08IaXn7zDwTvPqhfW7Ts/iNPuwe1Gg/qtE4nbdtssk4r7Qs/4Oqlje6LuFprw/R1Om1fMM46rbYv/ICr1zZsH1frbZi+TifuC8ZxteKGl6/Okd1YoO/lweGeP/5ilLNn0qvPKMajKPMF6P0I6A4V6YiziUp0yNlECR1zTgYp00Fni1ToqLNFqtx87yTLWZQdtbEDvlOC7m1lJ3xjXHzCZc0UN7Cl2yA3srXbIDexxdsgV9jqbZCb2fJtkFvY+m2QW9kCbpDb2ApukKtsCTfGrRNbww1yA1vEDXIjW8UNchNdxg2Cha7jBsGZLuQGwYWu5AbBlS7lBsGNruUGwUoXc2PgNtHV3CA40OXcIDiSg7/P/ZPUxyay+1Iqy9qLHZaf42L5ZY3vNmSiCu8LW6hK+8LGR1ZrtC9skZT2hQ0Srp05NAJKdXku9o4b2CHeKSO3m0Zuindq0GoTPXA75cvdznZQoWaDJ8E+pmfqG2SQ9+s6F586cy3OcvV8Me6muoogJlthiiHBTQT46lHEiIELjMAmAbiwiuolm/y4iurF5iePMMU2h0tEY+PyKsoT++rXUc7Y/OoRn9jmcAllbJyuol4xrz5MHvWKudwQVlF32MuNq6hTbH7yqEdsc4hHL2Lj8ioKEfvqyyoKEZtfPQoR2xzNowmxcbqKCsS8ekbCAjx3h0QrwHMxeuZUXFhuWkUvYi9XPHoOe7l5FRGEvdyyiojD5lePDsI2R/NoNmycrqNzMC8/TS4lgrngFFy6CZu3kpLENkByaRnsBcs64gt7wXkdFYH9A2UdHYT9A64JBxdM7hpxcIGn6ygFTAPI5MrlmwumdB/AK0jiOloM2wBpHbmB/QPikhvYFslU1WAxKIWb/Z3ea5l2vtG+NnCvSPjY/41KDv8+D2DFPrbR07/P43ihD1Y+vGtsUp48qOXIdsh81Z65Rr5sz0TxdXvVIPGFexYpc1O1ZULuEYcyw1pfpcZhv9zC78Y2786ncfhcIwhnkbmyVcH2bmnqCRVW64FYJvc07BfouR5qvzNmrU1wDSmchfg2tKur59EsXLjl0pInfmlvuXiiqzYuD7XL3NRwZajH6KZLcwVh7U1wBWFtnA417NzScMQUwtmCzCudiWLY0djd599LIdH+qWoWEgVXJ6JZ8HVL46ahlqWbLk08gWp737MnUG3jylD/z00NV4cagG66tOYJj9uboJ7wuIlzdRTSqzgrro5CehVnhegopIB3QfQQUsD3cc0h1Ks4K8QcQgVe4TNhEzsnu/9iey2itwuvQqtDzTk3NW4b6mi66dLUk2kw910nTx7ExoWx9qBbWk7jWH/QTdeWXPkYex98daw2L4+1Ad3UdsU/4Lr/7LpU2B+0etqOXjBtG+s0uqlp1ZVisa41TpMrBWTzwlgr1A1tF6c41lF007UlV+bI3gdxZbZsXh5rebqp7cpYe85N11bHuppuurbmae954R5RV67P5M2UftDo7FdbLdVvxpnkD5qdfWGFkR+e/bpKW04eA1u/cZ68yX2s8Ng+KPPpvWqgCp/Qs1D8NGgTRY+DTmqQ6HnQFinSA6FNUqDLgRXITEd8muaxHBjjJrocGOMKXQ6McTNdDoxxC10OjHErXQ6McRtdDoxxlS4Hhrj4FE6l9g0fyqnUvuEzOpXat5TocmCMK3w5MAbOfDkwBi58OTAGrnw5MAZufDkwBla+HBgCy8SXA2PgwJcDY+DIlwNj4ESWA0uEsPzUaHC9/NhoEFx4jZsC+rEolfdcDS9K+DnSJoofJG2hMj1JWoJBokdJmyR6lrRJSkOqLgnbfUsTsxBnC5qgQuA4E/NRU5vf8/sfxK6BiCel0qZ2rUOCs02X1hyqLnjL1aHxQuGuoYgn2dGWRvUJDMtVlhYdEi14S5JDTgbDZUgNtqlRs0MNBl93GVJDbXrddUhDtunSmkNZBW+JOlRgKNw1GvGkJNrSqDUMibg2XVp0iLjgLUkOSRcMlyEV1aZGzUPas02XVhwCL3hLqkPuBcPbkPhrU6OqQ/yFXrdPyKjXuG6fkPEqrgUjZKRdC0bWqDRcxnRRm1o1j+nJNl1b8Wis4F2pHkUYTG9jeq5N7aoegRV65TqNya22vHIdlDNtujbXGAB4V5JHaAbTZUxOtKld85hMbNO1uYYPwLtSPSI0mN7GpFCb2lXHJGQbri1REk3W10hT8Ii2YHrk5jNLIOcz734iOYcmg9HxNNG6KQHkWGmigvohXjjNxg8UOtllJF7SVOlkl4lqdLLLRCmd7Op3/k1hopNdFinQyS6LBPa/bbF/1/Vv5pBYsY8graxTEFbsA3IzK/YBuYUV+4Dcyop9QG5jxT4gV1mxD8bF5YpHsQ8IDrTYBwRHWuwDghMt9gHBQot9QHCmxT4guNBiHxBcabEPCG602AcEKyv2KQg2TbR05ny9qQ/mJ2FZb7bET8IyUfwkLBNFT8KSbJDoSVgmie63ZJIqK6IWpPt/mgkOX7xYU5Ry+jARzO1OyrrdDfGKZ3pD0u0WzO0Wx0ExNk0cB8VCOQ6KheIPSjVI/EGxSPxBsUhg275DZ7KMNE5LM7Ug5sw35IjgwsGjM1+RlwiuImxKcQPtzGPcSDvzGDfRzjzGFdqZx7iZduYxbuGdeQxceWceAzfemcfAyjvzELhMvDOPgQPvzGPgyDvzGDjxzjwGFt6Zx8CZdObP3xoGltfBn6+378wXXgdvvS8Lr4M3UbwO3kJVXgevBonXwVskXgdvkeiKyBwQZ36mp0Kd+YY58zWTznyOiK89kzKRznzDnPnqOCjWpjkOioVyHBQD1eiDko1ofKMPikmiD4pJSqQzL4gz38CEUCv9e7l/RBod6T4/1P2XSKMj3SCXjnSDXDrSDXLpSDfGVT7SDYL5SDcI5iPdIJiPdINgPtINgvlINwjmI90gmI90g2A+0g2C2Uj3+VO4i5WJj3Sfrzf1wXwAz3j/yMQH8EwUH8AzUXQALyeDdDo+n+//XOryJu1IezdNQ29Drv3+boILGY6ehbXeSnsWFqmxTT5yBlxwmWkaQBc8R8gFl5nGAXTBkanQMhM8cC74+3UbP+A4Q8amzcQPwO36MrvGuF93j/fd/ar9+xXXQpyOqrXiTB/VbJD4Q2SR+ENkkRrbicgkKRdfP7+3+0cGFzEcOgRlJGkmuIahhf7Do//mwiUMh3xARiZGC65gaEpxhf7kwbiZ/uTBuIX+5MG4lf7kwbiN/uTBuMp/8kBgQr0wUTtHqBcmausILcNE7R2hbJiozSPaMAVu8zL/yYOBC//Jg4Er/8mDgRv7ydMgrPKfPNCLg2jCJAveASF/kLqAAhWwBz+tIG0wRRLmYcvJUy2Q2F1EGFdY9A2/TwTD5jn2LWCskxZL5Gqsr9IOnEVqdEpDEVcLl0hU7btw/ROTJ/o7DetOK9n9QVWwD6oMHquX6aj4ucrgudq5D+zBytTB2v355ZOFzkcMh6AFdrT4AYlZjQWiOqTDwy9Cm9TYHq0FyRxKBr+/qmHN/lHANRGH1WakDZzgkohj8AbpWye4IuLQoRXk0kUbIJcu2gC5fCoL4/KpLIzLp7IwLp/Kwrh8KgviVkcqCwM7UlkY2JHKwsCOVBYGdqSyMLAjlYWBHaksDOxIZWFgRyoLA7OprIJ0aJXmSGVBL7qZJgP7gkKUCtIi+VUSobUm1nUqRn6rCftVUhLi5OAKjSMXSji2wn5LFKx0WWYaDe5bomA1xtIa+y2B3WHKeufQLYZLNQ5RjgIl7XClxpGboPXiQijjRu7vGq7TOHIzIIwSXKZxPMJG3gvXZdRE7VQhv6qQomrBNRnH1WL7TwdFClJ7KKps/gniZlyS0RLFDex3Fcil82Ugl86XgVw6XwZy6XwZyKXzZSCXzpeBXDpfBnL5fBkGDny+DATz+TIQzOfLQDCfLwPBfL4MBPP5MhDM58tAMJ8vA8H4B1uqxPs+4+0tTmDk1ZyJ/hY5EL5ZJvpb5EA4ZzmCX23pVbVekJRkjqDCPrU+1VgrfOaS9m1g7BpecGzcZsamgW5lPlmhz6G+1/KxBVsRI8+RI/iBVqb+/vSPFS4Ayaf96ZISqEosjbkrcblHDcz9M1N7oF/qWLeDnNDZPylShkB7lyVhzich9UiZMjB4kEKWyyeJkHbkxBx1WNqRC3OiEn+i+pn0LGBmuh5b1JYKBXuy0L3NihprhL3Ako8k4HbHu1yUSnHh91FRipvp5xTGLXRAAuPSeg+Qy6elMS6t/sC4mRYGg1w6MQ1y6cQ0yKUT0yCXTkyDXDoxDXLpxDTIpRPTIJdOTINcOjGNcQufmAbBfGIaBPOJaRDMJ6ZBMJ+YBsF8YhoE84lpEMwnpkEwn5gGwUrP+MTAhCQkUptHSEIitXmEJCRSm0dIQiK1eZWSN6ajfLJiWeCMK0MOfnvtZ9bzTAoCFNAdfOwaz+vnXipHd7j2sf8zFfuEKUqbojEXoPYF7E1hVgDmmU4EKTQ83Ifd32m3+8LF/u80splhY+3VAijqzfRWNDCWMrvf029I9UVuZEyyFkDam9GuH9mg9r+pG9UFviTaFqC2ZH5voOhKxpZAOzcyBAQaWqmjMrufQXPoxMXXz5fdD4hp4OK3FSlszUrHXypmAzr+AnLp+AvIpeMvIJeOv4BcOv4Ccun4C8il4y8Qt0x0/AXk0vEXkEvHX0AuHX8BuXT8BeTS8ReQS8dfQC4dfwG5dPwF5NLxF4wb+PgLCObjLyCYj7+AYD7+AoL5+AsI5uMvIJiPv4BgPv4Cgvn4Cwjm4y8YOPLxFxDMx19AMB9/AcF8/AUEC5l7h1z3EjOZKYZ894I3ITloY6oCOf2CNyE5aGMqUoFdiAkqB60AuGClU/zYihNdJnDOzX0uXSbQAmKIRPZJaBGyQuKqfBpS6lTw7iOH0oMWoNVmlluRCqpC9B5JlboZKlk5A+4ar6QEbzK2JAe7H4TXUWI3hPA6SuyOYLuSNPnZ57DnC+lNXETY28paHtsgAVwf1bH71IOlVahVRBEwdXDqvvJC7rMa13Yi0otVtGVGfrvaj7c39893f+3TC19/3H17un943v2tv++evv86am1fqrrzJ0pupbWfP/8ff/NdwQ==基本ユニット
搬入側
貨物車から素材を取り出して、パッシブ供給チェストに詰め込みます。

搬出側
要求チェストから取り出して、貨物車に詰め込みます。
また要求チェストの物流要求に、このハブグリッドの素材と数を設定しておきます。

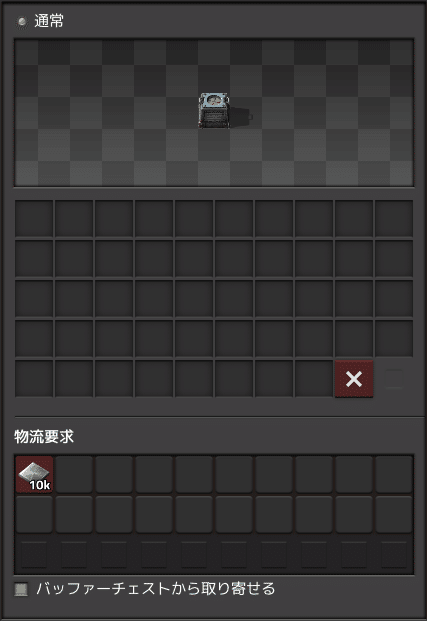
搬入側チェストから搬出側チェストへ素材の移動
基本ユニットで書いた内容からもわかるように、パッシブ供給チェストから要求チェストへ物流ロボットを使って気合で素材を移動させます。
1つのハブグリッドの物流ネットワークに物流ロボットを500体くらい入れています(もっと入れた方がいいかも)。
最初はベルトテクニックを使ってハブグリッドを実装していましたが、専有面積が広くなるのと遅いので、最終的には物流ネットワークを使った気合で移動に落ち着きました。
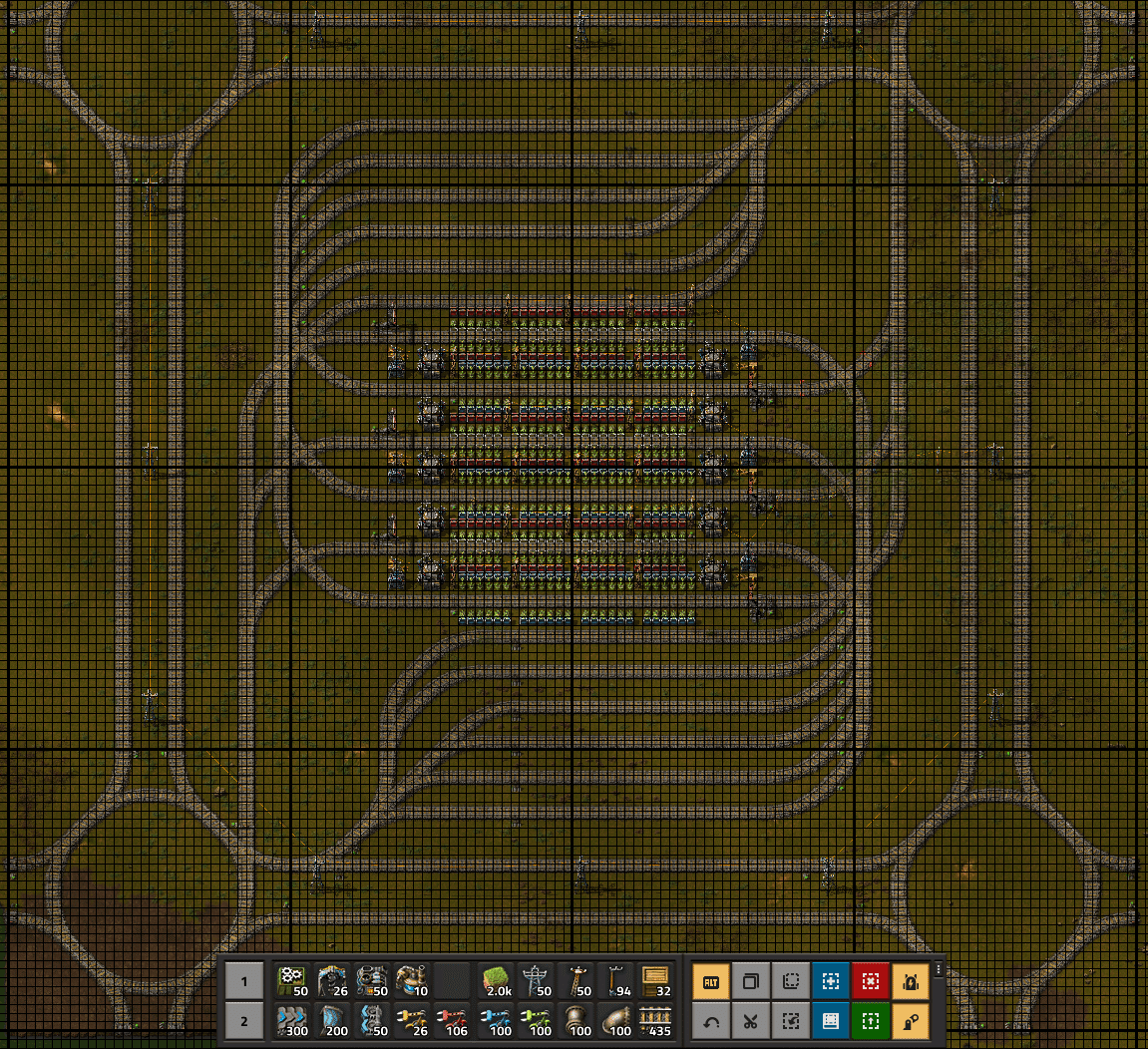
その他:同名駅
搬入側駅と搬出側側の駅をグリッドの中にそれぞれ3つずつ入れて同名駅としています。
これによって最大3つの列車が同時に積み込み、積み降ろし可能になっています。
その他:待機線
ハブグリッドの周辺が混みやすくなるので、待機線をハブグリッドの中それぞれ6本ずつ作って、周辺の混雑を緩和させています。
まとめ
グリッドの疎結合化を促進させて、素材の過不足を簡単に把握するためにハブグリッドを作ってみました。
もっといい形があると思うので是非教えてください!
実際に動いている例
鉄板、銅板、鋼材、電子基板、発展基板の5つのハブグリッドが動いている状況が以下の例になります(動画の方がわかりやすいのですが、静止画ですみません)。
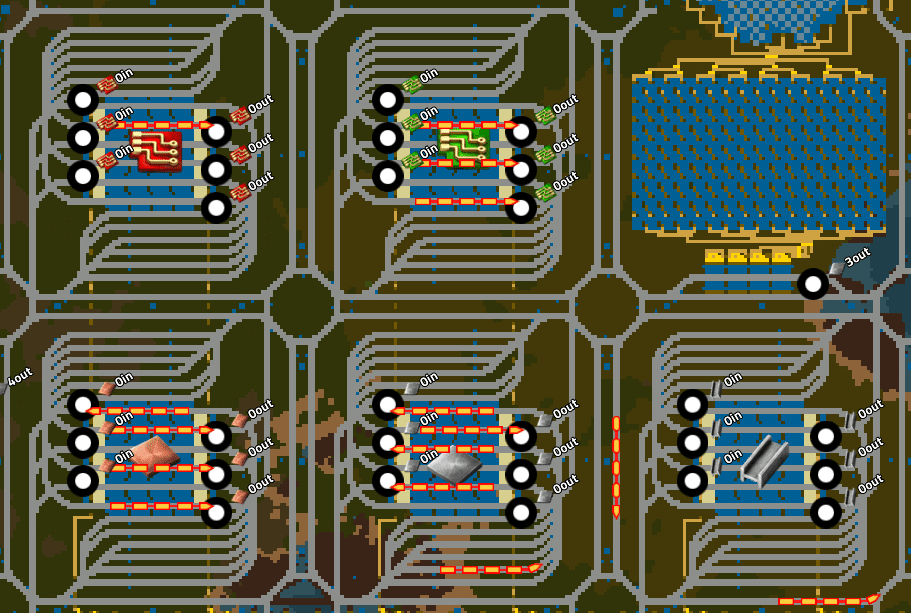
同名の in駅(搬入側駅)、out駅(搬出側駅)が素材ごとに3つずつあります。
鉄板ハブグリッド
in駅に3両、out駅に1両、in駅の待機線に1両とまっている
→ 鉄板は余っている銅板ハブグリッド
in駅に1両、out駅に3両とまっている
→銅板は不足している鋼材ハブグリッド
in駅にもout駅にもとまっていない
→需要供給がそこそこ安定してそう電子基板ハブグリッド
out駅に3両とまっている
→電子基板が不足している発展基板グリッド
out駅に1両とまっている
→発展基板が少し不足気味
こんな感じにハブグリッドの状況を見るだけで、各素材の過不足が簡単に把握することができ、改善に向けた次のアクションを簡単に見つけられるようになります。
課題
駅の数を3駅、待機線の数を6本としていますが、駅の数を4駅にしてもよいかもしれません。また駅の数は5駅まで増やせると思いますが、5駅にすると待機線が作れなくなったと思います。
駅の数と待機線の最適なバランスは不明です(全体の系のバランスによって違いそう)。
また、ハブグリッドの中の駅の数をさらに増やしたいときは、ハブグリッドをもう1つ用意するか、グリッド1つの大きさを大きくするかになるでしょうか。
