
ベイズ統計モデリング~2群間の平均値に差はあるのか~
現在、統計検定準1級の勉強に取り組んでいます。統計の勉強をするにつれて、ベイズ統計の面白さにはまりつつあります。そんな日々を送っているなかで、今後はベイズ統計で学んだことをこのnoteにアウトプットしていこうと考えています。
本記事を執筆するにあたり参考にしている書籍は、↓の書籍です。
この書籍の第6章の内容を参考にして、空想上での研究データを疑似的に作り、そのデータにてベイズ統計モデリングを適用しました。
想定した研究データとは、本を読んだ後(Reading)に行ったテストのスコアと、筋トレ(Exercise)後に行ったテストのスコアです。イメージとしては↓の図となります。なんでこんなイメージをしたかというと、私が博士課程の時に運動と脳機能の研究をしていた際に良く見慣れた研究計画なため、実際に統計を行う際に理解が深まると考えたからです。おそらく読んでいる皆さんにとっては分かりづらいかもしれません。。。まあ、簡単に言うと、2つの異なるグループがあり、そのグループで得られたスコアを用いるといった感じです。

この2つのグループ間でのテストのスコアの平均値のさがどれほどあるのかというのをベイズ統計モデリングで検証していきます。一般出来な統計で言うところの対応なしのt検定に該当するところだと思います。
この疑似データとしては、Readingのグループは平均点が50点で標準偏差が5となるような正規分布から乱数を発生させています。Exerciseのグループでは平均点が70点で標準偏差が5となるような正規分布から乱数を発生させています。
データのヒストグラムとしては↓のようになります。
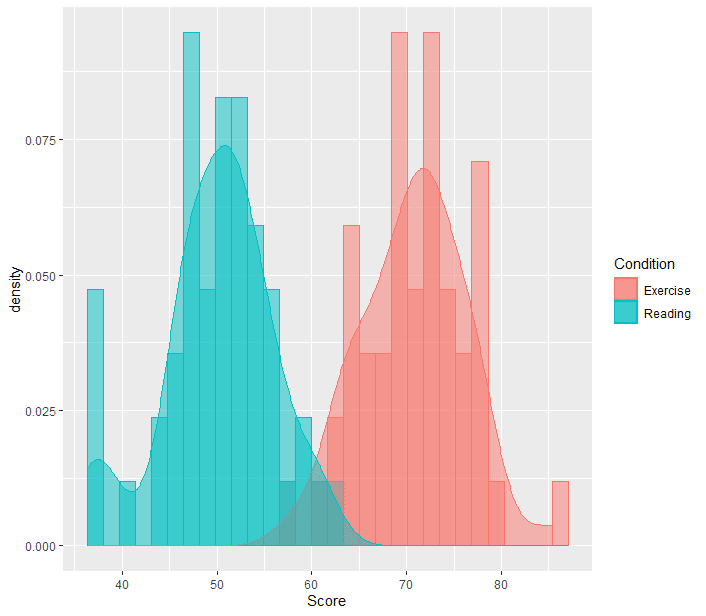
図からすでにExerciseのほうが点数がいいのが明確ですね。今回は統計の結果が分かりやすくでるようにこのような疑似データとしました。
早速コードを書いて結果を見てみました。コードに関しては、「実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門」のp147~p150(第6章の6.8)に記載されているコードを使いました。ということでここでは、コードの記載は省略します。
結果をみてみると、

diffにおいて95%信頼区間である箇所を確認すると、ExercsieグループとReadingグループでは平均値が18点から23点ほど差があることが分かりました。このことから、本を読んだあとにテストを行うよりも筋トレしたあとにテストを行ったほうが良いという解釈につながりますね。ただ、今回は疑似データなので、実際のところは分かりません。
モデルの収束に関するRhatは1であり、収束したモデルが作成できたと考えられます。トレースプロットを描いてみると、↓のような感じになりました。

バーンイン期間を含めたトレースだと↓のようになりました。

とこんな感じで今日のところは終わりにしようと思います。ここまで淡々と書いていますが、実際はエラーの嵐でこのような簡単な統計モデリングのコードを実行するだけでも一苦労しました。プログラミングと人生にエラーはつきものなので受け入れるしかないですね。次回は回帰モデルに挑戦していきます。
最後まで読んでいただきありがとうございました。
参考文献
・馬場真哉 (2019).「実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門」講談社
