たかが50km、されど50km

先の記事「エリア探訪には自転車が良いと気が付いた」で、付近を乗り回すだけでは飽き足らず、と書いた。

実際、どのくらいの範囲で乗っていたのかというと、我孫子から銚子が80km強で最も長い。往復170kmを超えました。

その他では我孫子から鹿島神宮まで60km強。
筑波山まで約50km。
千葉駅までが約40km。
東京駅までが約35km

だいたい50km圏内といったところでしょう。
往復だと100km圏内となります。

私の脚力では、信号の少ない郊外で平均時速15km（都心では10km）と計算していますので、往復100kmでは7～8時間乗ることになります。

明るいうちに帰ってくるとなると、日照時間が12時間として、往路4時間、4時間ステイ、復路4時間というイメージでしょうか。

毎週末あちこちでかけているうちに結構行き尽くしたと思っていたのですが、この50km圏内がなかなか奥深い、という意見もあります。

わが街周辺にも一度も通ったことのない道は確かに数多く存在する。
果たして50km圏内の道をすべて制覇するには、何kmくらいかかるのか。

自転車に乗りながらふとそんな妄想にかられたことがあります。

イメージとしては、

この図で縦横の線として表されている道路の距離を求めよ

みたいな問題。
結構厄介だな、家に帰ってEXCELで計算するか、とも思ったのですが、ふと

サークルではなく正方形のエリアだとどうだろう？
これなら暗算で十分解ける。

200mのメッシュだとして、縦横50kmのエリアに各々50÷0.2＝250本の50km道路がある。
つまり、総道路長は(250＋250)×50km＝2.5万km。

ここからさきのサークルをあてはめると、

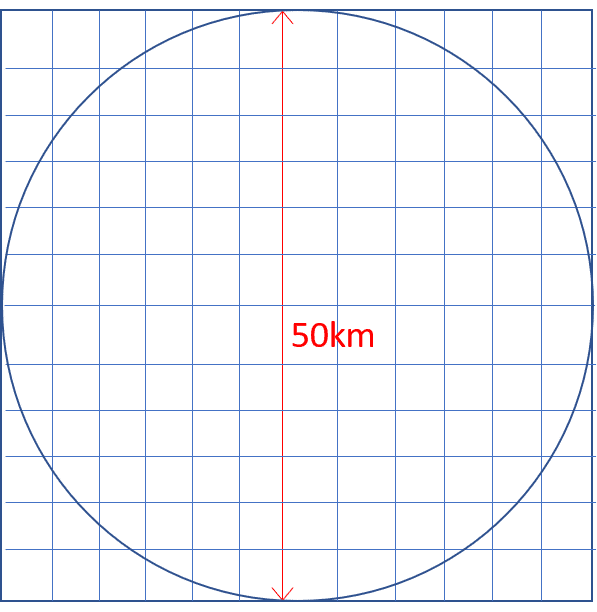
50kmサークル内の総道路長は、この正方形と円の面積比にほぼ等しいはずだから、円の面積＝半径×半径×3.14＝正方形の1辺/2×正方形の1辺/2×3.14...
つまり正方形の面積の 3.14÷4 。
暗算での細かい計算は苦手なので、だいたい8割と考えて、50km圏の道路を制覇しようとしたら、2万km走破となる。

えっと、地球の一周が約4万キロだから、地球半周分？
それは奥深いわ。

どうも仮定が悪すぎる気がする。
碁盤の目状の道路は50kmのエリアに広がっていないよね。

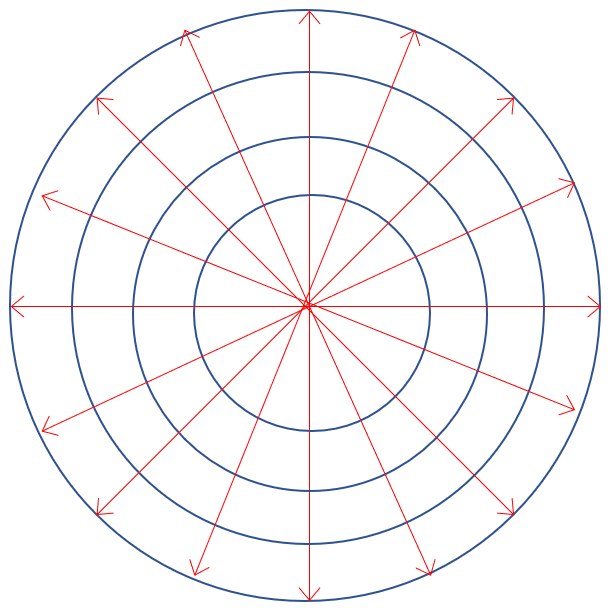
で、放射線モデルで考えてみる。
とりあえず12本の放射線状道路と、10kmおきの環状線だとどうなるか。

円周は直径×3.14だから、環状線部の総道路長は、(50＋40＋30＋20)×3.14。
それに放射線状部の総道路長は、12×50km
合わせて、1,020km。（暗算なので3.14は3とおいた）

本州の全長が1300kmくらいあるとのことなので、それに近い数字ですね。
日本のどの地域かにもよるが、このモデルの真ん中あたりは碁盤の目状なので、すべての道を走破となるとこれより長い。

なるほど50km圏内は奥深いのかも。

✳︎放射状道路の図には16本あるように見えるが、錯覚です。

ウソです。本当は12本作るつもりが、勢いで16本になってしまいました。まぁ16本だとすると道路が200km長くなって、本州全長とほぼ同じになることになりますが。