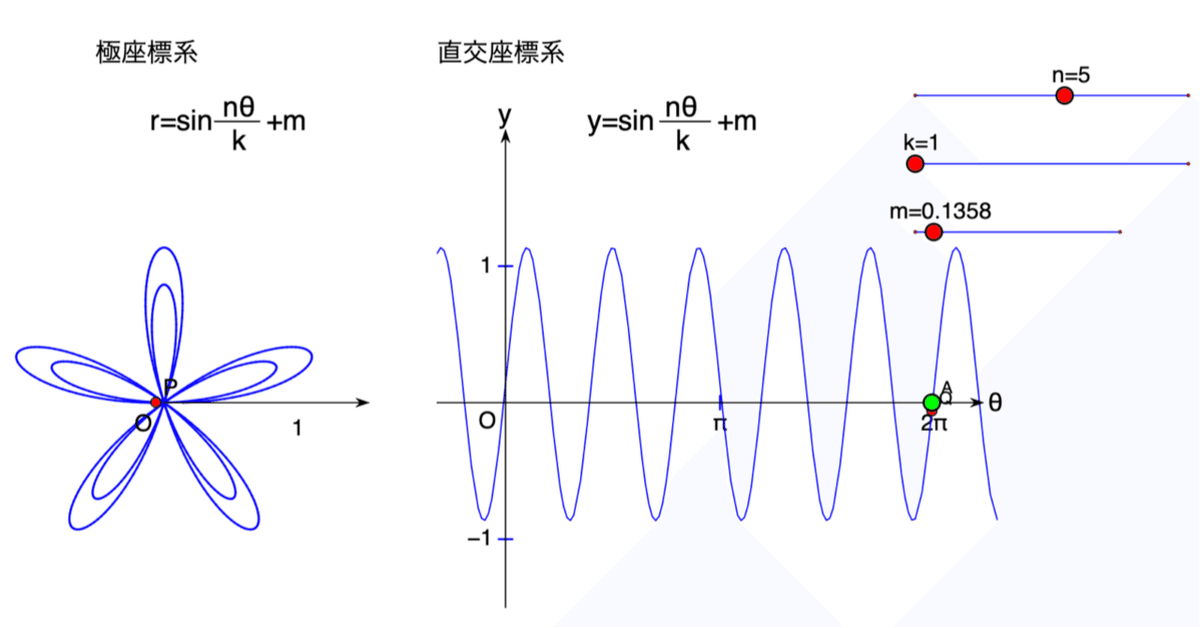
Cinderellaで花を描く:花びら(2):正葉曲線の描かれ方
直交座標系での y=sin2θ のグラフと極座標系での正葉曲線 r=sin2θ
極方程式 r=sin(nθ) で正葉曲線が描かれる様子を確かめます。まず, sin(nθ) の値がどんな動きをするのかを、おなじみの直交座標でも見てみましょう。それを見ながら,極座標系での r=sin(nθ)のグラフを考えます。そうすることにより、「なぜ n が偶数のときは2n枚、奇数のときはn枚なのか」もわかりますし、さらに新しい疑問も生じるでしょう。たとえば、「 定数を足して sin(nθ)+m とするとどうなるだろうか」などです。それがわかると、さらに新たな疑問も出てくるでしょう。これが面白いところです。
さて、ここで基本的なことを確認しておきます。
極座標系では、点の位置を極からの距離rと、始線からの回転角θで表します。rは距離ですから正の実数です。しかし、極方程式で曲線を描くときは、rが負の場合も認めるということです。rが負の場合は数直線と同様、負の向きに、すなわち、弧度法で θーπ の向きに点を取るということです。
このことを確認した上で、まず r=sin2θ を考えてみましょう。
直交座標系での y=sin2θ のグラフは次のようになります。
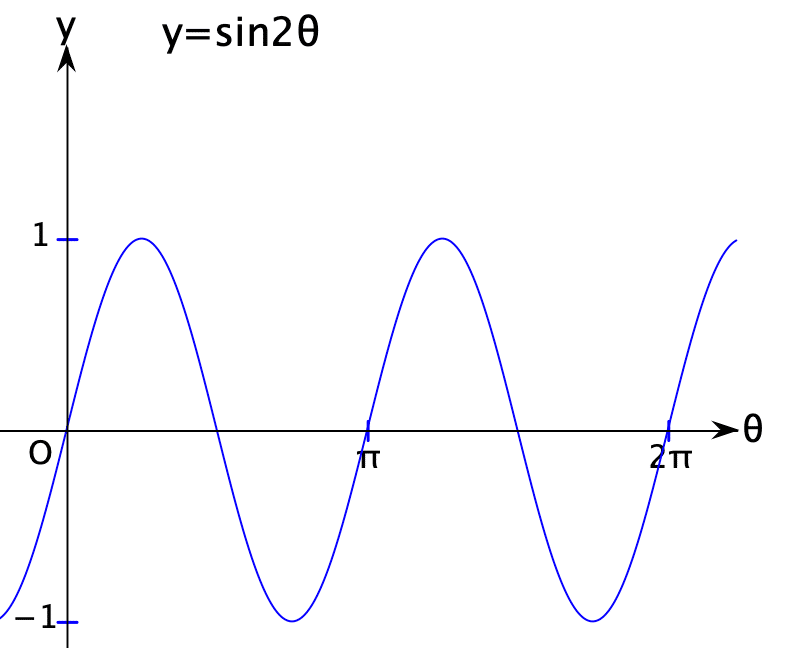
sin2θの値は、0→1→0→ −1→0 を繰り返します。それに対応して,極座標系で極方程式 r=sin2θ であらわされる曲線はどのように描かれていくでしょうか。
次の図は左側に極座標系,右側に直交座標系を描いています。

右側の点Aはθの値を表しそれに対応して点Qがグラフ上の点を表します。
今,θ=0です。θの値を少し大きくしてみましょう。

点Qのy座標が sin2θ の値で,緑の線がそれを表します。上の図では$${\theta=\frac{\pi}{4}}$$ です。yの値は1なので,左の極方程式の図形の r=1 に対応しています。緑の線の長さは同じです。
次の図は $${\theta=\frac{\pi}{2}}$$ で,y, r の値は0です。
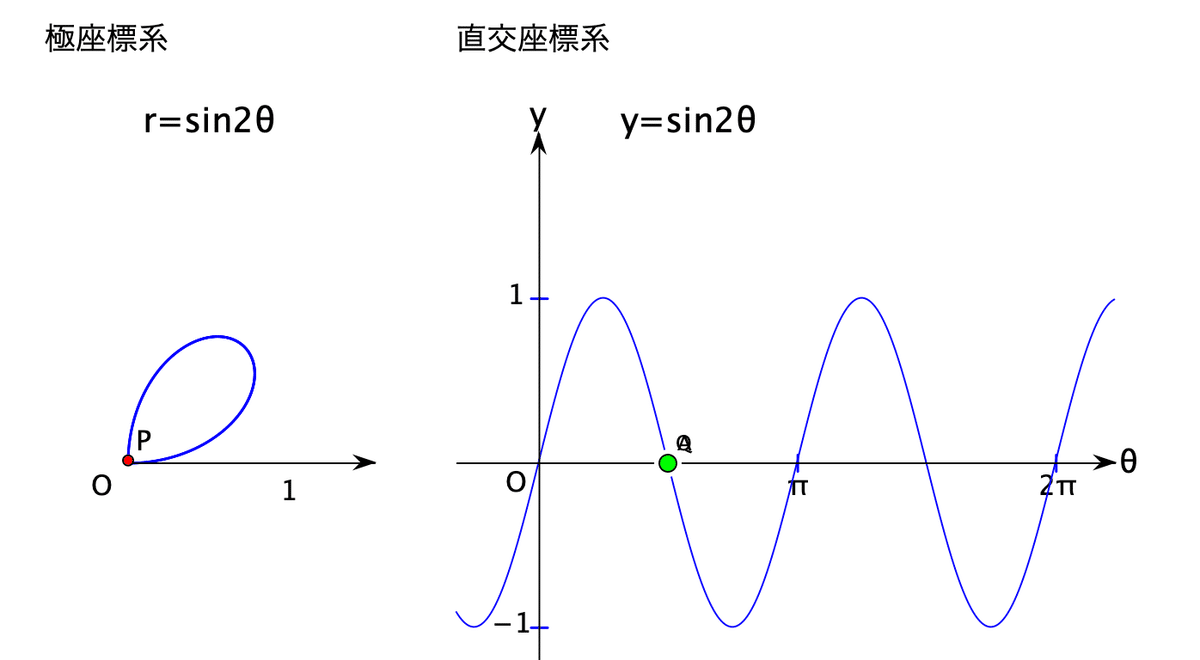
さらに進むと,yの値は負になります。次の図では,y, r の値が負なので,極座標での点Pの位置は,θ-π の位置に来ています。
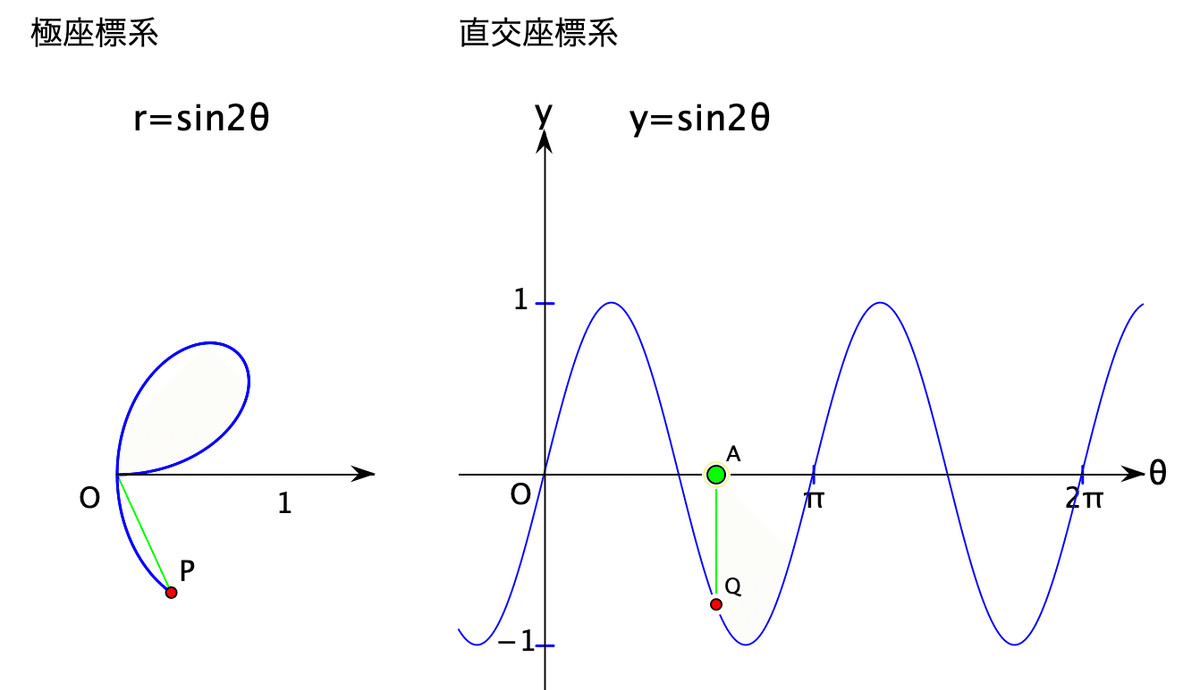
θ=π になると,y=r=0 なので,点Pは極に戻り,ここまでに葉(花びら)が2枚描かれたことになります。

さらに進むと,y, r は正なので,点Pは次の位置に来ます。

さらに進みましょう。

かくして,θが0から2πまで変化すると,葉(花びら)は4枚描かれることになります。r=sin2θの葉の数は2×2の4枚です。
では、nが奇数の場合はどうか、r=sin3θで確認してみましょう。

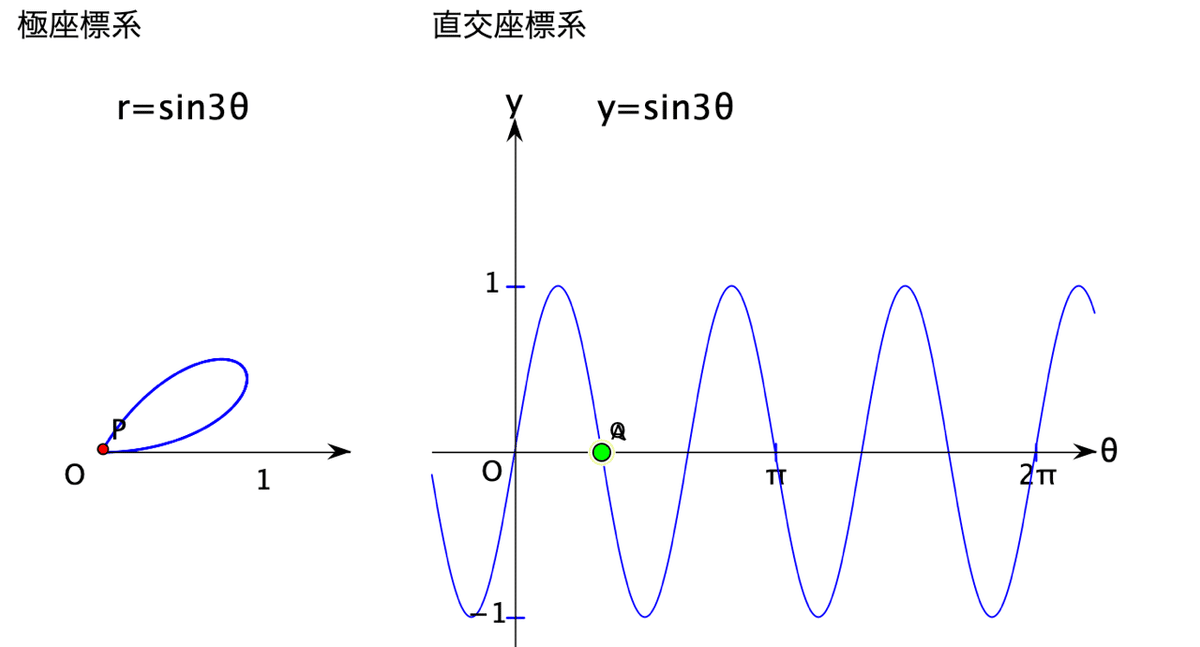



πまでに描いたものを次の2πまでにもう一度描いていくことがわかります。3θで葉は3枚ですが、1枚の葉を2回描いていたのですね。
r=sin(nθ)+m が描く図形
r が負の場合も図が描かれることがわかりました。では、r が負にならないような方程式ならどうなるでしょう。−1≦ sin(nθ) ≦ 1 ですから,r=sin(nθ)+1 とすれば、rは負になりません。まず、直交座標系で y=sin2θ+1 のグラフを描き、yの値の動きから、極方程式 r=sin2θ+1 が描く図形を想像してみましょう。
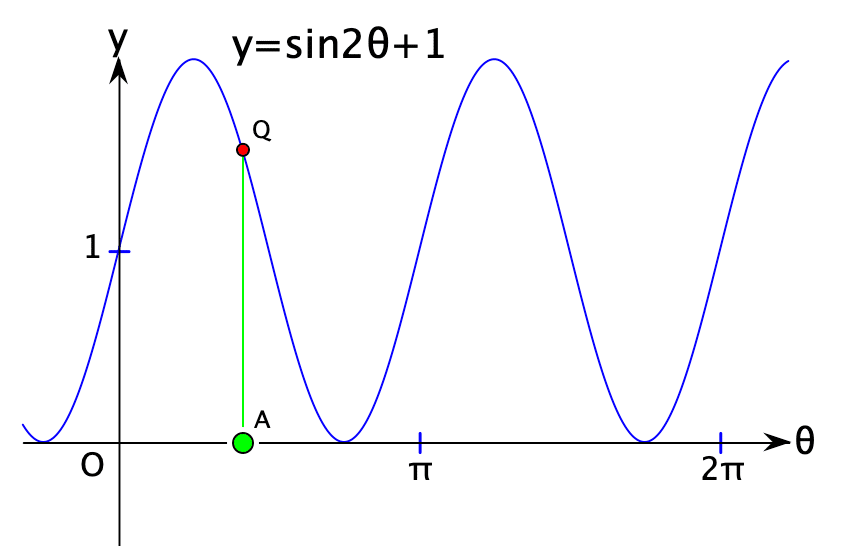
まず、θ=0のとき、r=1 ですので、出発点は極座標の ( 1 , 0 ) です。$${θ=\frac{3}{4} \pi}$$ のときr=0になりますので、ここまでで葉が1枚描かれるはずですが・・いや、1枚にはなりませんね。出発点が ( 1 , 0 ) ですので閉じた図になりません。では、次のπまでの間に描かれるのでしょうか。
いや、r > 0 ですから( 1 , 0 )の方には戻りません。となると?
次のようになります。
極方程式 r=sin2θ+1 が描く図形は、次のような双葉になります。
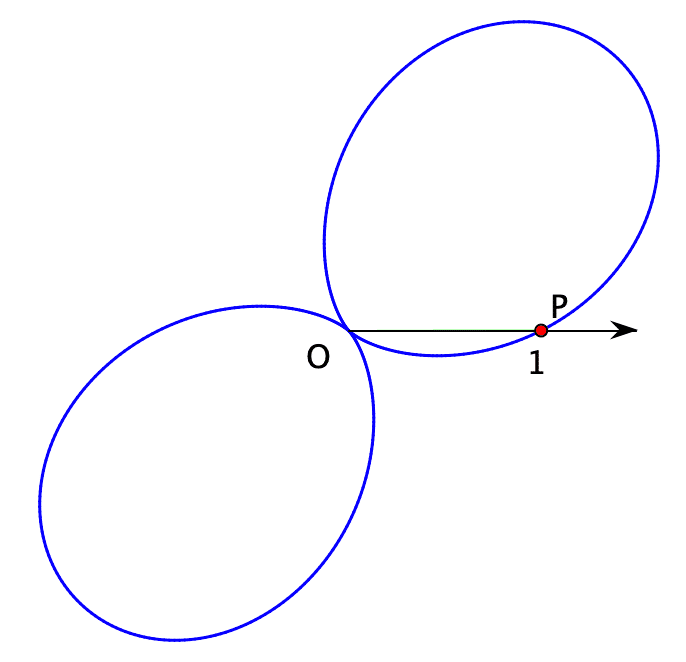
微妙に傾いていますね。描き始めの点( θ=0 のときの点 ) が ( 1 , 0 ) だからです。
ここまでわかると、一般に r=sin(nθ)+m がどのような図形を描くかも想像できるようになるでしょう。
では、nを分数にしたら?
想像するだけでなく、それを確かめるためにツールを作りました。パラメータの値をスライダで変更していろいろ試してみましょう。(タイトル画面は一例)
