
「情報関係基礎」教材化(1):2017年三角形の個数
大学入試センター試験「情報関係基礎」2017年の問3を教材化する。
最初にこれを取り上げたのは,図形を表示しなくてもよいので,import するライブラリは Numpy だけであること,全体のコードが短いこと,なじみのあるテーマで生徒の興味を引きやすいことである。
全体のコードが短いので,力のある生徒なら難なく読めるだろう。授業で実際に取り扱ったが(言語はCindyScript)お互いに相談しながら積極的に取り組んでいた。
教材化にあたり,元の問題をそのままやるのでなく,授業向けにテキストをつくり変えた案を示す。
もとの問題
三角形に頂点から対辺に線を引く。たとえば次図で,三角形はいくつあるかを数える。手で数えようとするとなかなか難しい。答えは15個。
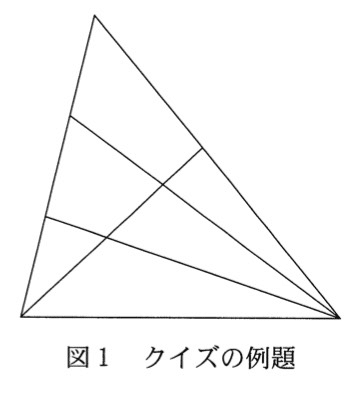
これをプログラミングで解決する。
まず,そのアルゴリズムの説明があるのだが,これがなかなか興味深い。
問題は設問も含め,丁寧に書かれているが,ここではその要点だけを書いておく。
図2のように,三角形の頂点と線分の交点に番号をつけ,辺と線分に記号をつける。
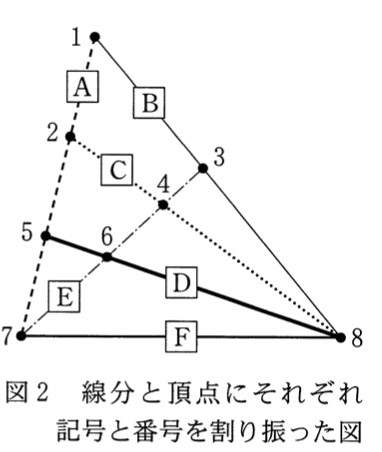
この頂点・交点の番号を使って,たとえば (1,2,8) で三角形が表現できる。この三角形の3つの辺は,(1,2),(1,8),(2,8) と表される。かっこの中は左を始点,右を終点とする。(1,2) は始点1から終点2に引いた線分である。始点の方が必ず小さい数とする。
あるpを共通の始点とする2つの辺(p,q),(p,r)について,qとr を結んで三角形ができるかどうかを考えよう。辺(p,q)と(p,r)が同一線分上になく,かつ,組(q,r)が辺であれば三角形ができる。

たとえば,(1,2),(1,8) の場合,(1, 2), (1,8) が同一線分上になく,かつ,(2,8)がC上にあるので三角形になる。
そこで,2つの頂点(交点)の組み合わせ(順列)をすべて調べ,それぞれがA〜Fのどの線分上にあるかを調べた表を作る。
まず,準備として,表1の,各辺の始点・終点と線分との関係(組み合わせ)の表を作る。たとえば,(1,2) は線分A上にあり,(1,3)は線分B上にあるが,(1,4)を結ぶ線分はないので,除外され,次のようになっていく。
ウ,エ は問題の空欄
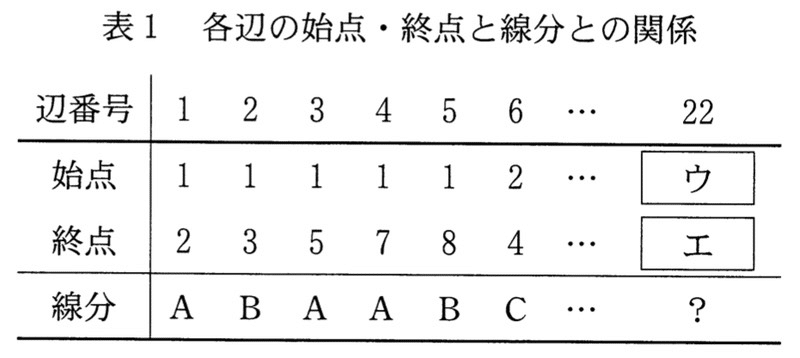
この表ができたならば,共通の始点とする2つの辺(p,q),(p,r)について,(p,q), (p,r) が同一線分上になく(q, r) が辺上にあれば三角形ができると判定できて,できる三角形の個数がカウントできる。
表1を作るために,すべての頂点の組み合わせについて,表2で表される2次元リスト(配列) Hen を用意する。

Hen[i,j] の要素は,頂点の組 (i,j) が辺ならばその辺がある線分の記号とし,辺でない場合と,i ≧ j の場合は "-" とする。
以上のような説明の後,表1を作るプログラムと,三角形の個数を求めるプログラムが次のように問題として出される。いくつかの空欄を穴埋めする形だ。

しかし,実際にこのプログラムを実行しようと思えば,問題になっている部分のコードだけでなく,頂点と辺の番号と名前の設定をし,リスト Hen を作っておかなければならない。まさか,リストHen を手作業で作るとは思えないから,そのためのプログラムが必要になるが,それらは教員が作って実習用のファイルを用意することになる。
配列のインデックスの問題
教材化にあたって,配列のインデックスが0からか,1からか,という問題もある。この2017年の問題ではインデックスは1からだ。しかし,共通テスト試行問題を見ると,共通テスト「情報Ⅰ」のDNCLではインデックスが0からになるようだ。Pythonでもインデックスは0からだ。ここをどうするか。方法は2つある。
(1) インデックス0を使わない。
(2) 番号などを0からに変えて問題を作る。
どちらでもよいが,(1) の場合,データを作るのに,インデックス0にダミーの要素を入れ,配列のサイズを1だけ大きくしておく必要がある。問題を解くだけならよいが,新しいデータを生徒に作らせるとなると,ここがネックになりそうだ。
そこで,(2) の方向で,問題文そのものも作り替えることにする。頂点の番号を0スタートにするのだ。
教材案
三角形に頂点から対辺に線を引く。たとえば次図で,三角形はいくつあるかを数えよう。
(少し時間をとって数えさせる。答えは8個)

では,見つけた8個を,次のルールで分類してみよう。
<ルール>次のように三角形の頂点,線分の交点に0から番号をつける。
できた三角形をこの番号で表す。ただし,番号は小さいほうから書く。
(生徒に作業をさせ,板書などで確かめる)
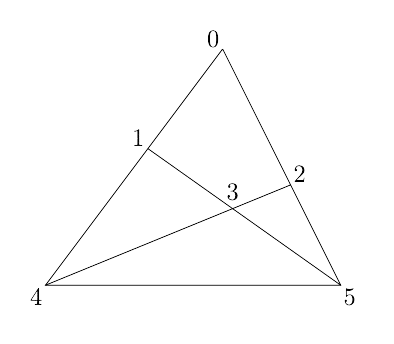
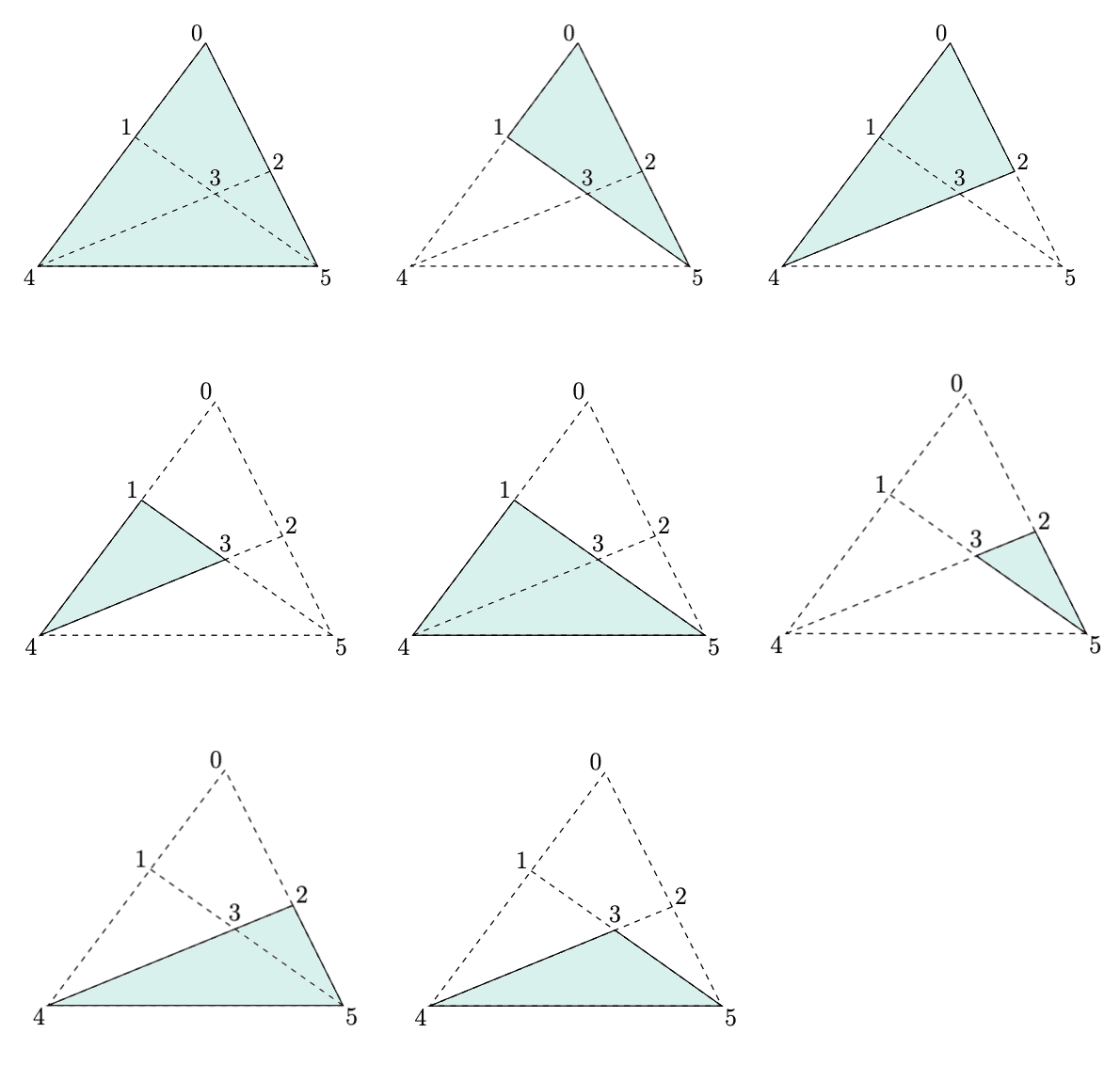
このうち,頂点が0であるものに着目しよう。頂点0と他の点の組み合わせ(順列)は次の5通りだ。
(0, 1), (0, 2), (0, 3), (0, 4), (0, 5)
このうち2つをとって,三角形ができるかどうかを考えよう。上の図で確かめると,三角形になっているのは次の3つの場合だ。
(0, 1 )と(0, 5),(0, 2)と(0, 4),(0, 4)と(0, 5)
5つの組み合わせから2つをとる方法は10通りある。その中で三角形ができるのはこの3通りだ。では10通りのおのおのについて,三角形ができる条件はなんだろう。
(答:3点が同一直線上にないことと,他の点を結んだ線分があること)
これを一般的に次のように表そう。
あるpを共通の始点とする2つの辺(p,q),(p,r) (p<q<r) について,3点 p, q, r が同一直線上になく,かつ,組(q,r)が辺であれば三角形ができる。
たとえば,(0,1),(0,2) の場合,0, 1, 2 は同一直線上にないが,(1, 2) を結んだ線分はないから,三角形 (0, 1, 2) はできない。(0,1),(0,5) の場合,0, 1, 5 が同一直線上になく,かつ,(1,5) を結んだ線分があるので三角形(0, 1, 5) ができる。
したがって,0から5までのすべての順列について,以上のことを調べれば,何個の三角形ができるかがわかる。
表を作る
これを表を作って調べていこう。辺に次のように名前をつけておき,2点を結ぶ線分が乗っている辺の名前を書き,なければ「ー」とする。たとえば,(0, 1) はA,(1, 4) もAである。
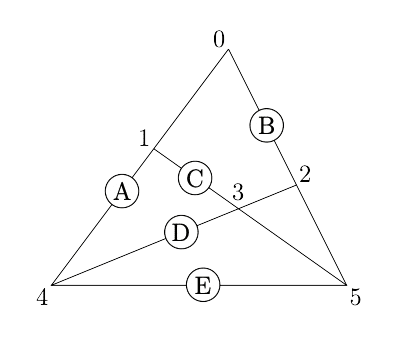

(表1)
この表をリスト Hen(i,j) で表す。実習用のファイル「sankaku.py」では,辺の名前などのデータと,このリストは作ってある。
次に,ここから,2点を結ぶ線分がいずれかの辺上にあるものだけを拾い出して次の表を作る。9番目以降は省略している。まず手作業で全部作ろう。

(表2)
これを2次元リストとしてもよいが,内容がわかりやすいように,始点,終点,線分ごとの1次元のリストとする。組み合わせは添え字の番号で決めることができる。 リストは Siten : 始点,Syuten:終点,Senbun:線分 の3つで,たとえば,Siten[0]=0 , Shuten[0]=1,Senbun[0]="A" である。辺(線分)の総数(リストの要素数)をhensosuとする。 これを作るのが,次のプログラムである。一部が空欄になっている。
hensosu = 0
for i in range(tyotensu-1):
for j in range(i + 1,tyotensu):
if Hen[i][j] != :
Siten[hensosu] =
Syuten[hensosu] =
Senbun[hensosu] =
hensosu = hensosu + 1
print(hensosu)
print(Siten)
print(Syuten)
print(Senbun)
実習用の「sankaku.py」を開いて,このプログラムを空欄を補充して完成し,実行しよう。hsnsosu の値が何になるかは先ほど手作業で数えてあるはずだ。それでプログラムが正しく動いているかどうかを確かめよう。また,表示されたリストの内容を表2と比べて確かめよう。次のように表示されれば正しくできたことになる。
13
[0 0 0 0 1 1 1 2 2 2 3 3 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[1 2 4 5 3 4 5 3 4 5 4 5 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
['A' 'B' 'A' 'B' 'C' 'A' 'C' 'D' 'D' 'B' 'D' 'C' 'E' '' '' '' '' '' '' ''
'' '' '' '' '' '' '' '' '' '' '' '' '' '' '' '']
次に,三角形の個数を求める。三角形ができる条件は「3点 p, q, r が同一直線上になく,かつ,組(q,r)が辺(線分)である」であった。まず表2から,2つの線分を取る。たとえば,(0, 1), (0, 2) を取ると,表1から(1, 2) を結ぶ線分は「ー」となっているから三角形はできない。(qをi,rをj で読み替える)(0, 1), (0, 4) を取ると,表1から(1, 4) を結ぶ線分は「A」となっているから三角形ができる。こうして個数を数える。そのためのプログラムが次の部分である。三角形の個数を kotae に格納する。
kotae = 0
for x in range(hensosu - 1):
y =
while Siten[x] == :
if Senbun[x] != and Hen[Syuten[x]][Syuten[y]] != :
kotae = kotae + 1
y =
print("三角形の個数は" + str(kotae) + "個である")
空欄を補充して完成しよう。正しくできれば8個と表示される。
準備
生徒が考えればいいのは,前述の教材中の空欄である。繰り返しと条件判断,リストへの値の代入ができればよい。
しかし,教材中にあるとおり,事前にこのファイル「sankaku.py」を用意しておかなければならない。用意するものはつぎのもの。
・リストHen を作るための元のデータ。
・リストHen を作る部分。
それが次のプログラムだ。
import numpy as np
Onseg=[ # 頂点1から順に,その頂点を通る線分の名前を書く
["A","B"], # 0
["A","C"], # 1
["B","D"], # 2
["C","D"], # 3
["A","D","E"], # 4
["B","C","E"] # 5
]
tyotensu = len(Onseg) # 点の個数
# Siten,Syuten,Senbun を用意し,Henを作成する
Siten = np.full(tyotensu * tyotensu,0)
Syuten = np.full(tyotensu * tyotensu,0)
Senbun = np.full(tyotensu * tyotensu,"")
Hen = np.full((tyotensu,tyotensu),"-")
for i in range(tyotensu):
for j in range(tyotensu):
if i < j :
for p in range(len(Onseg[i])):
if Onseg[j].count(Onseg[i][p]) > 0:
Hen[i][j] = Onseg[i][p]
print(Hen)
# --- 表2を作る ---- ここで,それぞれのリストを用意し,すべての要素を "-" にするために np.full(要素数,要素) を使った。
また,「Onseg[j].count(Onseg[i][p]) > 0」は,Onseg[j] に Onseg[I][p] が含まれているかどうかを調べるリスト処理だ。含まれていれば正になる。
これら,リスト処理に関することはPythonの入門書には載っていないかもしれない。リスト処理について生徒に詳しく説明する必要はないが,何をしているのかくらいは説明してもよいだろう。
実行すると,最後の print(Hen) で,表2が表示される。
これで準備はOK。ファイルを配布し,テキストは印刷しておく。
プログラムの全体を示しておこう。なお,データとして,もとの問題のものを Onseg1 として用意してある。
import numpy as np
Onseg=[ # 頂点1から順に,その頂点を通る線分の名前を書く
["A","B"], # 0
["A","C"], # 1
["B","D"], # 2
["C","D"], # 3
["A","D","E"], # 4
["B","C","E"] # 5
]
Onseg1=[ # センター試験のもの
["A","B"], # 0
["A","C"], # 1
["B","E"], # 2
["C","E"], # 3
["A","D"], # 4
["D","E"], # 5
["A","E","F"], # 6
["B","C","D","F"] # 7
]
tyotensu = len(Onseg) # 点の個数
# Siten,Syuten,Senbun を用意し,Henを作成する
Siten = np.full(tyotensu * tyotensu,0)
Syuten = np.full(tyotensu * tyotensu,0)
Senbun = np.full(tyotensu * tyotensu,"")
Hen = np.full((tyotensu,tyotensu),"-")
for i in range(tyotensu):
for j in range(tyotensu):
if i < j :
for p in range(len(Onseg[i])):
if Onseg[j].count(Onseg[i][p]) > 0:
Hen[i][j] = Onseg[i][p]
print(Hen)
# --- 表2を作る ----
hensosu = 0
for i in range(tyotensu-1):
for j in range(i + 1,tyotensu):
if Hen[i][j] != "-":
Siten[hensosu] = i
Syuten[hensosu] = j
Senbun[hensosu] = Hen[i][j]
hensosu = hensosu + 1 # この位置に入れる
print(hensosu)
print(Siten)
print(Syuten)
print(Senbun)
# ----- 個数を数える -----
kotae = 0
for x in range(hensosu - 1):
y = x + 1
while Siten[x] == Siten[y]:
if Senbun[x] != Senbun[y] and Hen[Syuten[x]][Syuten[y]] != "-":
kotae = kotae + 1
y = y + 1
print("三角形の個数は" + str(kotae) + "個である")リストのインデックスを1からにする
始めに述べたように,もとの問題ではリストのインデックスは1からになっている。三角形の頂点に番号を付けるのも,1からの方が自然に思われるかもしれない。Pythonに限らず,リスト(配列)のインデックスが0から始まる言語は多いので,これに慣れるためにも,番号を0からとした。もし,「1から」にするならば,「要素数は n+1 にして第0要素は使わない」とすればよい。繰り返しも range(1,tyotensu-1) のようにすればよい。そのように変更したものが次のプログラムである。
import numpy as np
Onseg=[ # 頂点1から順に,その頂点を通る線分の名前を書く
[], # 0
["-","A","B"], # 1
["-","A","C"], # 2
["-","B","D"], # 3
["-","C","D"], # 4
["-","A","D","E"], # 5
["-","B","C","E"] # 6
]
tyotensu = len(Onseg) # 点の個数
listsize = tyotensu
# Siten,Syuten,Senbun を用意し,Henを作成する
Siten = np.full(listsize * listsize,0)
Syuten = np.full(listsize * listsize,0)
Senbun = np.full(listsize * listsize,"")
Hen = np.full((listsize,listsize),"-")
for i in range(listsize):
for j in range(listsize):
if i < j :
for p in range(len(Onseg[i])):
if Onseg[j].count(Onseg[i][p]) > 0:
Hen[i][j] = Onseg[i][p]
print(Hen)
# --- 表を作る ----
hensosu = 0
for i in range(1,tyotensu-1):
for j in range(i + 1,tyotensu):
if Hen[i][j] != "-":
hensosu = hensosu + 1
Siten[hensosu] = i
Syuten[hensosu] = j
Senbun[hensosu] = Hen[i][j]
print(hensosu)
print(Siten)
print(Syuten)
print(Senbun)
# ----- 個数を数える -----
kotae = 0
for x in range(1,hensosu - 1):
y = x + 1
while Siten[x] == Siten[y]:
if Senbun[x] != Senbun[y] and Hen[Syuten[x]][Syuten[y]] != "-":
kotae = kotae + 1
y = y + 1
print("三角形の個数は" + str(kotae) + "個である")生徒の実習としては,どちらでもできるが,新しく三角形を作って,Onseg を作り替えるときに,第0要素に何かを入れておく必要があり,ここで生徒がつまずく可能性がある。生徒の状況などを勘案してどちらでやるかを考えるとよいだろう。
