
Cinderellaで数学:いろいろな曲線:ドロネーの高次曲線作図器
この記事は,「曲線の事典」(礒田正美他著・共立出版)に基づいて書いています。
ドロネー(M.N.Delaunay)は,クランクを用いた作図器を用いて,2次曲線や4次曲線を描いています。2次曲線(円錐曲線)については,次のページに書いています。
4次曲線
一辺が長さ $${a}$$ の菱形 CPQDが与えられている。CA,CBは,図のように軸PC,CDを延長した線分であり,CA = CB = $${b}$$ である。また,点A,Bは直線 s 上を動く。点 P が円周上を動くとき,点Qは4次曲線をかく。

この図をCinderellaで作図します。描く手順はいろいろあるでしょう。以下は一例です。
まず直線 s をx軸にとります。背景の軸に合わせて直線を加えるツールで直線を引きます。y軸は不要ですが,点Pが動く円をy軸上に中心をおいて適当なところに作図します。円上に点をとります。これが動点になります。

次に,円周上に取った点Dを中心とするあまり大きくない円と,x軸と交わる円の2つを描き,x軸との交点の左側の点を取ります。元の図のAになります。また,Dとこの点(E)を線分で結んで,小さい方の円との交点を取ります。元の図のCになります。(作図上はF)

平行線を加えるツールで,Fを通りx軸に平行な直線を引き,円とのもう一方の交点を取ります。また,鏡映ツールを選択し,鏡になるものとしてこの直線,鏡に映すものとして点Dを選択すれば,これで菱形の4点ができたことになります。
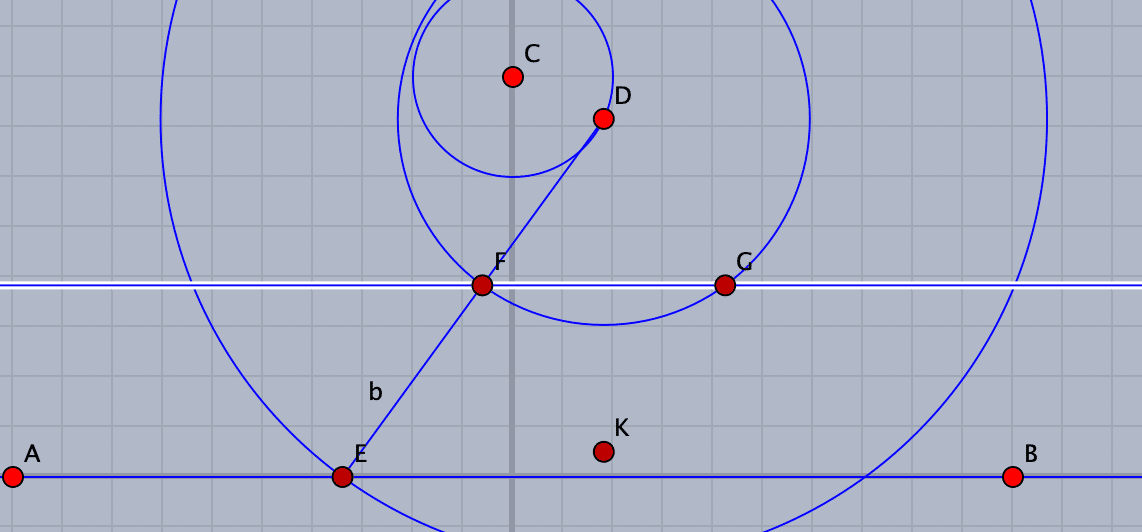
それぞれ線分で結んで菱形を作りましょう。
次に,Fを中心に半径FEの円を描き,x軸との交点をとれば,これが元の図のBになります。FとLを線分で結ぶと,菱形の点Kもこの線分上に乗った形になります。

軌跡ツールを選んで,動かすものとして点D,軌跡を描く点として点Gを選ぶと軌跡が描かれます。

おや,本の図と違いますね。これは,菱形とCAの長さの関係でこの図になるのです。補助円の大きさを変えて,元の図の比率に近くなるようにすれば,本の通りの軌跡ができます。

うまくいったら,点の名前や大きさを変えたりして体裁を整えましょう。
Web上でインタラクティブに補助円の大きさを変えて軌跡の変化を見ることのできるものを作りました。軌跡の描画は,解説にある式を使いました。
P$${(x,y)}$$,Q$${(x',y')}$$ とすると
$${x'=x+a \sqrt{1-\dfrac{y^2}{'a+b)^2}}, \ y'=\dfrac{b}{a+b} y}$$
トーラスの切断図形
平面上に,一辺の長さ $${a}$$ の菱形ABCDがあり,頂点B,Dは直線 s 上を動く。軸PB,PDは長さ $${b \ (b>a)}$$ であり,点Pは点Qを中心,半径 $${r}$$ の円 $${\gamma}$$ 上を動く。点Pが円$${\gamma}$$ 上を動くとき,頂点A,Cは円$${\gamma}$$ が非線形変換された曲線をかく。この曲線は直線 s と点Qの距離によって形が変わり,カッシーニの卵形線と呼ばれる様々な曲線をかく。
特に,点Qと直線 s の距離 $${d}$$ が$${d=\sqrt{b^2-a^2}-r}$$ のとき,ベルヌーイのレムニスケートをかく。この装置によって,円環面(トーラス)の中心軸に平行に切ったときにできる様々な切断面に現れる図形をかくことができる。

この図をCinderellaで作図します。描く手順はいろいろあるでしょう。以下は一例です。
まず直線 s をx軸にとります。背景の軸に合わせて直線を加えるツールで直線を引きます。y軸は不要ですが,点Pが動く円をy軸上に中心をおいて適当なところに作図します。円周
上に点を取ります。これが動点になります。この点を中心とし,x軸と交わる円を描き,交点をとります。

Dを通り,x軸に垂直な線を引き,EまたはFを中心とした円を描いて,垂線との交点をとります。これで菱形の4頂点がとれました。

各点を線分で結んで菱形ができたら,軌跡ツールを選び,動かす点としてD,軌跡を描く点としてHを選びますと軌跡が描かれます。

この軌跡は菱形の対角点も通りますが,y軸上に取った円の位置や補助円の大きさを変えて軌跡が2つに分かれるとき,一方しか表示されないときは,軌跡を描く点としてもう一方を選びます。
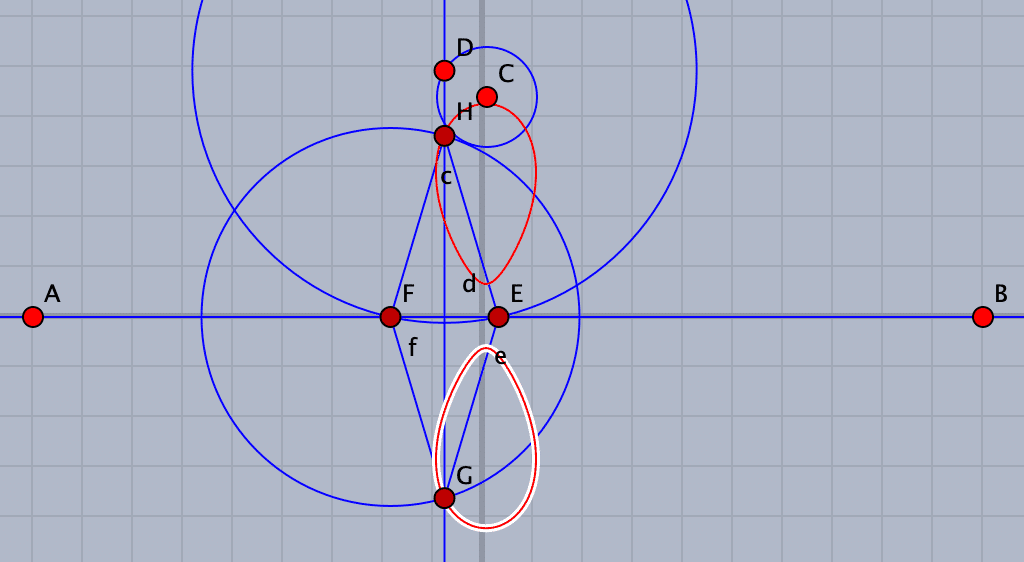
補助円の大きさなどをうまく調整すると上下がつながってレムニスケートになります。

うまくいったら,点の名前や大きさを変えたりして体裁を整えましょう。

Web上でインタラクティブに補助円の大きさを変えて軌跡の変化を見ることのできるものを作りました。軌跡の描画は,解説にある式を使いました。
P$${(x,y)}$$,A$${(x',y')}$$ とすると,
$${x'=x, \ y'=\pm \sqrt{y^2-a^2-b^2}}$$
作図器を模したものを作りました。
