プログラミング：ドキュメントを残す

2021年2月19日 07:14

document：記録

円周上で正方形をころがすプログラム，初めは500行くらいになった，と書いた。
　それを整理して210行くらいになった。
　そのあと，円の半径を変えられるようにしたものを作り，円の半径は一定で，円周の長さと多角形の周長が同じ場合について作った。この時点でさらに整理して短くなっている。
　次は，扇形をころがした。
　この間に，さらに整理が進んで，100行くらいになった。あとのときのためにコメント文も書いたが，ここまでまとめていくと，やっていることがソースを見ただけではわからないようになってきた。どのように状況を分類し，どのようにコーディングしたのか。コメント文だけでは書ききれない。説明するために図が必要になるからだ。
　そこで，「考え方」を文書に残すことにした。以前にもやったことがある。ソースだけではわからないことがらをドキュメントで残しておく。以下は，その内容である。（ややこしい部分もあるので，読み飛ばしも結構）
　なお，ドキュメントそのものは PDF で残してある。

===============================

円周上で多角形を転がす　考え方

円周上を，すべることなく多角形を転がしたとき，多角形のある頂点が描く軌跡を表示する。
初期位置と回転方向をどのようにするかを決める。
直線上を多角形が左から右へ転がっていくときとの類推から，次のようにした。

　　　　直線上を多角形が転がる　　　　　　　　円周上を多角形が転がる

状況を分析する

円周上を多角形が転がるとき，２つの状態がある。
(1) 辺と円が接しながら回転する

(2) 頂点だけが円周上にあって回転する

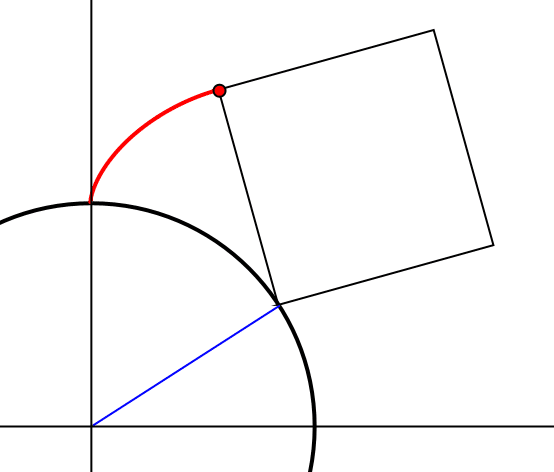
初期状態から始めて，(1),(2) を交互に繰り返しながら進むことになる。

これに，状態として①，②，③，・・・　と番号をつけていくと，奇数番は(1)，偶数番は(2) の状態になる。

① 　　　　　　　　　 ②　　　　　　　　　　③　　　　　　　　　　　　④

また，最初に着目した頂点の位置は，番号が進むにつれて時計回りに進んでいく。

(1) と (2) では，多角形の描き方が異なる。
多角形を一つの頂点から始めて，時計回りに頂点をとって線分で結ぶものとしよう。次の図は正方形の場合である。

(1) では時刻の変化とともにP1の位置が変わるが，(2) ではP1の位置は変わらない。
また，(1)では辺P1-P2の向きが円の接線方向であるが，(2)では辺P1-P2 の向きが変化する。
そこで，多角形の描画を次のように関数にする。

多角形を描画する関数を作る

polygon(no,pt,v)
引数：no 位置の番号
　　　pt 頂点P1の位置
　　　v　辺P1-P2の向きを表す単位ベクトル
戻り値　no に対応した頂点の番号：着目点の多角形内での位置

頂点の位置はリストにする。引数 pt , v によって，頂点P1,P2の位置が決まる。

vertex=[pt,pt+L*v]; // 頂点リスト

P3の位置はP1-P2をP2を中心に多角形の内角分回転すればよい。回転には，回転行列を用いるのが一般的だが，現在の教育課程では，高校では行列を学ばないので複素数を用いる。図は五角形の場合である。

vertex=[pt,pt+L*v]; // 頂点リスト
repeat(N-2,s,
z1=complex(vertex_s);
z2=complex(vertex_(s+1));
z3 = z2+(z1-z2)*(cos(Th1)+i*sin(Th1));
vertex = append(vertex,gauss(z3));
);

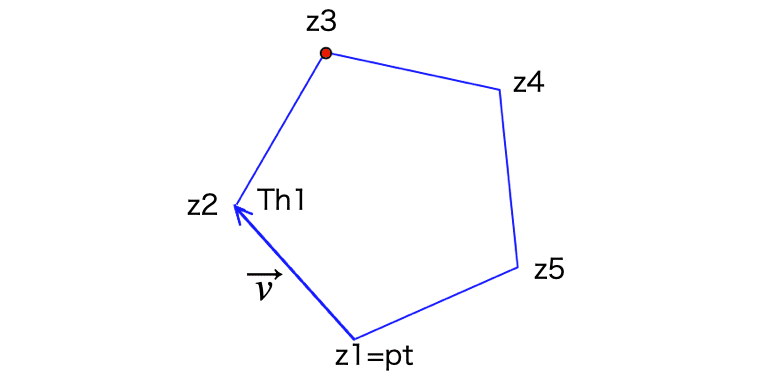
complex(p) は点pの座標を複素数に変換し，gauss(z) は複素数zを点の座標に変換する組み込み関数。append でリストに追加する。
以下，次々に回転しながら他の頂点を求めていけばよい。

頂点リストを結んで多角形を描く。CindyScriptでは drawpoly() で多角形を描くことができる。

drawpoly(vertex);

次に戻り値である。
戻り値は，①②ではP2，③④ではP3，・・・と一つおきに変わっていく。正方形の場合，P2，P3，P4，P1，P2，・・・とサイクリックに変わっていく。これを天井関数 ceil() と，剰余を求める関数 mod() を用いて，次のように計算する。

eno = mod(ceil(no/2),N)+1; // 戻り値の要素の番号

かくして，多角形を描く関数を次のように作ることができる。

polygon(no,pt,v):=(
vertex=[pt,pt+L*v]; // 頂点リスト
repeat(N-2,s,
z1=complex(vertex_s);
z2=complex(vertex_(s+1));
z3 = z2+(z1-z2)*(cos(Th1)+i*sin(Th1));
vertex = append(vertex,gauss(z3));
);
drawpoly(vertex);
eno = mod(ceil(no/2),N)+1; // 戻り値の要素の番号
ret = vertex_eno;
);

次に，状態①と②での引数の渡し方を考える。

状態①での引数の渡し方は次のようになる。
接点Pは辺P1-P2上にあり，辺P-P2の長さと，いま進んできた弧の長さが等しい。
ここから，点P1の位置を計算する。また，方向ベクトルvは接線方向である。

状態②での引数の渡し方は次のようになる。
点P1は変化しない。これまでに進んできた弧の長さから決まる。
P1からP2への方向ベクトルは時刻とともに変化する。

奇数番目の状態を描く関数を作る

状態①，③，・・・　すなわち奇数番目を描く。
引数として，初めからの回転角ではなく，この状態にはいってからの回転角を th として渡す。

drawpolygonodd(no,th):=(
len = R*th-L; // 動いた弧の長さと辺の長さの差：負になる
t=pi/2-(no-1)/2*L/R-th; // 接点の位置を表す角
p = R*[cos(t),sin(t)]; // 接点
p1 = rotatepoint(p,pi/2,len); // 正多角形の辺の端点P1
z = complex(p);
v1=gauss(z*i); // 接線方向のベクトル
polygon(no,p1,v1/|v1|);
);

ここで，rotatepoint(p,th,len) は，べクトルpの終点を始点とし，pをth だけ回転させた，長さlen のベクトルの終点（位置）を返す関数で，次のように定義してある。 len<0なら逆向きの位置になる。

rotatepoint(p,th,len):=(
z1=complex(p);
z2=z1+z1*(cos(th)+i*sin(th))/|z1|*len;
gauss(z2);
);

偶数番目の状態を描く関数を作る

次に偶数番目。接点がP1で，はじめ接線方向に辺があったのを時計回りに回転していく。その回転角を，引数 th で与える。

drawpolygoneven(no,th):=(
len = L; // 1辺の長さ
t = pi/2-no/2*L/R; // 接点の位置を表す角
p1 = R*[cos(t),sin(t)]; // 接点が多角形の1辺の端点になる
p2 = rotatepoint(p1,pi/2-th,len); // 回転角の分だけ接線方向から回転
v1 = p2-p1;
polygon(no,p1,v1/|v1|);
);

no 番目の図を描く関数を作る

これらを用いて，状態①，②の番号を no として，no番目の図を描く関数を作る　。no が奇数か偶数かで，drawpolygonodd(no,th) か drawpolygoneven(no,th) のいずれかを呼びだす。そのときに，現在の状態での角 th を求めておく。

drawfig(no):=(
d = floor(no/2)*L/R+(ceil(no/2)-1)*Th0; // Th0 は多角形の外角
th = theta-d; // d は前の状態までに回った角
if(mod(no,2)==1,
p = drawpolygonodd(no,th);
,
p = drawpolygoneven(no,th);
);
draw(p,size->3,color->[1,0,0]); // 着目点を表示
Pt = append(Pt,p); // 軌跡を描く点のリストに追加
);

この中でわかりにくいのが，前の状態までに回った角 d の計算だろう。
no が奇数（たとえば５）の場合，「前の状態までに」というのは ①②③④ である。
　奇数番目の状態では，辺と円が接するので，その間に進む角は floor(no/2)*L/R である。floor は床関数で，引数を超えない最大の整数をあらわす。floor(no/2) は no=1,2,3,4,5,・・　に対して0,1,1,2,2 ・・となっていく。noが5なら floor(no/2) は２で，今までに２回，奇数回があったことになり，その間に進む角が floor(no/2)*L/R である。
　偶数番目の状態では，多角形の頂点が円周上にあり，その間に進む角は多角形の外角分である。たとえば，no=1,2,3,4,5,・・・　に対して，それまでの偶数番目の状態は 0,0,1,1,2,・・・　回ある。これが (ceil(no/2)-1) で求められる。ceil は天井関数なので，no=1,2,3,4,5,・・・　に対して 0,0,1,1,2,・・・　となっていくのである。

　この部分は，はじめからこのような計算式でやっていたわけではない。とりあえず動くものを作るために，if 文の連続でやっていたのを，あとで整理したのである。

　これで道具は揃ったので，時刻（角）を進めながら描いていく。時刻（角）の取得はスライダでインタラクティブに行う方法と，コンピュータの内部時計を用いて行う方法があるが，今はその点にはふれない。いずれかの方法で，角を表す変数 theta を0から変化させていくものとする。

メインプログラム：角の進行に従って図を描く

角 theta を０から動かしながら図を描いていく。前述の通り２つの状態が交互に現れるので，角の大きさによってそれを分類していく。

if(theta<=L/R,drawfig(1)); // 弧長が辺の長さLになるまでが ①
if(L/R<theta & theta<=L/R+Th0,drawfig(2)); // 外角分回るまで　　　②
if(L/R+Th0<theta & theta<=2*L/R+Th0,drawfig(3)); // 次に弧長がL分 ③
if(2*L/R+Th0<theta & theta<=2*L/R+2*Th0,drawfig(4));
if(2*L/R+2*Th0<theta & theta<=3*L/R+2*Th0,drawfig(5));
if(3*L/R+2*Th0<theta & theta<=3*L/R+3*Th0,drawfig(6));
if(3*L/R+3*Th0<theta & theta<=4*L/R+3*Th0,drawfig(7));
if(4*L/R+3*Th0<theta & theta<=4*L/R+4*Th0,drawfig(8));
　以下適当なところまで続ける

これで動くが，この if の連続を何とかしたい。初めの方を，あとの方と同じ形式にすると次のようになる。

if(0*L/R+0*Th0<theta & theta<=1*L/R+0*Th0,drawfig(1));
if(1*L/R+0*Th0<theta & theta<=1*L/R+1*Th0,drawfig(2));
if(1*L/R+1*Th0<theta & theta<=2*L/R+1*Th0,drawfig(3));
if(2*L/R+1*Th0<theta & theta<=2*L/R+2*Th0,drawfig(4));
if(2*L/R+2*Th0<theta & theta<=3*L/R+2*Th0,drawfig(5));
if(3*L/R+2*Th0<theta & theta<=3*L/R+3*Th0,drawfig(6));

L/R と Th0 の係数に着目すると，一番左は 0,1,1,2,2,3,3,・・・左から２番目は 0,0,1,1,2,2,・・という列になっている。これは先ほど drawfig で考えた列の形だ。そこで２つの変数 m , nを用意して，mをL/Rの係数，n を Th0 の係数とし，m は 0,1,1,2,2,3,3,・・ n は 0,0,1,1,2,2,・・となっていくようにする。
さらに，& の右側の m, n の値の和が drawfig() に与える数になっている。
ここまで分析できれば，次のように繰り返し処理で drawfig() を呼びだせばよい。

drawcircle([0,0],R,size->3,color->[0,1,0]); // 半径Rの円を描く
tm = 0;
tn = 0;
repeat(8,
if(tm*L/R+tn*Th0<theta,tm=tm+1);
if(tm*L/R+tn*Th0<theta,tn=tn+1);
);
drawfig(tm+tn);

繰り返しの回数は適宜。ずっと動かすわけではないので，どこまで動かすかで設定すればよい。

Cindyscriptでは，スロットという概念があり，描画面上でマウスクリックなどのイベントが起きたり，内部時計を取得して時刻が変わったときのタイミングに実行されるコードは Draw というスロットに書く。プログラムの実行時に一度だけ実行すればよい関数定義などは，Initialization というスロットに書く。したがって，このコードを Draw スロットに書けばできあがりである。
なお，スライダを用いたり，内部時計を利用して，角 theta を変化させるためのものは別途用意することになる。

以上。