
Cinderellaで数学:いろいろな曲線:パシオッティ−オッディの円錐曲線作図器
「曲線の事典」(礒田正美他編著:共立出版 2009)に掲載されている,パシオッティーオッディの円錐曲線作図器です。
まず,説明の文章と,放物線の図を示しましょう。
パシオッティーオッディの作図器は,次のような機構である。長方形の枠組みABCD と直線LMが与えられており,辺AB 上に点Gがある。直線LM 上の点Iから直線 ABに直交する直線を引きこの直線と辺AB との交点S,辺CDとの交点をHとする。さらに、∠HIE =45°となる点を辺AB上にとり、直線HI上に ∠EFG=90°となるように点Fをとる。点Iが直線LM 上を動くとき、直線LMと直線ABとの交点の位置関係に応じて、点F は円錐曲線をかく。
作図器の写真と,放物線の場合の解説図です。

写真はWeb上の曲線の事典のページからダウンロードしました。本ではモノクロですが,カラーの方がわかりやすいのでこちらにしました。右図だけでは構造がわかりにくいでしょう。
Cinderellaでこれを描くために,文章の説明と,作図器の写真から,自由点と従属点を明らかにしていきます。自由点とは,作図後に自由に動かすことができる点で,その位置によって他の点(従属点)の位置が決まり,軌跡も決まります。さらに,Cinderellaの「軌跡」ツールを使って軌跡を描くために,「動かす点」と「軌跡を描く点」がどれになるのかを明らかにしていきます。
説明文は,作図器の説明であると同時に,そのあとの,軌跡が円錐曲線になる理由を説明するために点に名前を付けています。したがって,Cinderellaで作図するときには,必ずしもとらなくてもよい点もあります。たとえば,点Sは不要です。また,作図上では補助線が必要になるものもあります。
それでは次の点を考慮して作図していきましょう。
① まず,長方形ABCDを描きます。適当な大きさで描いておきましょう。頂点の4点は自由点です。
② 直線LMを適当に描きます。L,Mは自由点で,直線の傾きを変えることができます。作図したら,インスペクタで,点の名前をL,Mに変えておきます。
③ AB上に点Gをとります。AB上だけを動く(インシデント)自由点です。
④ LM上に点Iをとります。LM上だけを動く(インシデント)自由点ですが,この点が軌跡を描くときの「動かす点」になります。
⑤ このあとは,すべて条件を満たすようにとる従属点です。
I を通る,ABに垂直な直線を引きます。解説図には交点H,Sがありますが,これは不要です。交点をとる必要はありません。
⑥ 「∠HIE =45°となる点を辺AB上に」とります。点Hは作図していませんが,ここでは45°という角が大切です。方法はいくつかあるでしょう。たとえば,I を中心に円を描き,2本の直線との交点をとって,その中点をとります。中点とIを結べば45°の角をなす直線が引けますので,ABとの交点をとります。
⑦ 「直線HI上に ∠EFG=90°となるように点Fを」とります。たとえば,EGを直径とする円を描いて交点をとれば90°になります。

軌跡ツールを選び,動かす点として I,軌跡を描く点として F を選びます。直線LMをABに平行になるようにすると軌跡は放物線になります。

点 I と G の位置により,放物線の開きや位置が変わります。

解説によると,
SF =y,SG=x, SI=ES=2pとおくと、上式は$${y^2=2px}$$でと放物線を表す。
となっています。点Gが放物線の頂点になり,Gを動かしても放物線は平行移動するだけですが,直線LMの位置を変えると p の値が変わるので放物線の開きが変わります。
なお,Cinderellaの軌跡ツールでは放物線全体が描かれますが,実際の作図器では棒の可動域が制限されているので,描かれるのは一部です。楕円や双曲線も同様です。
直線LMの傾きを変えると,楕円や双曲線になります。
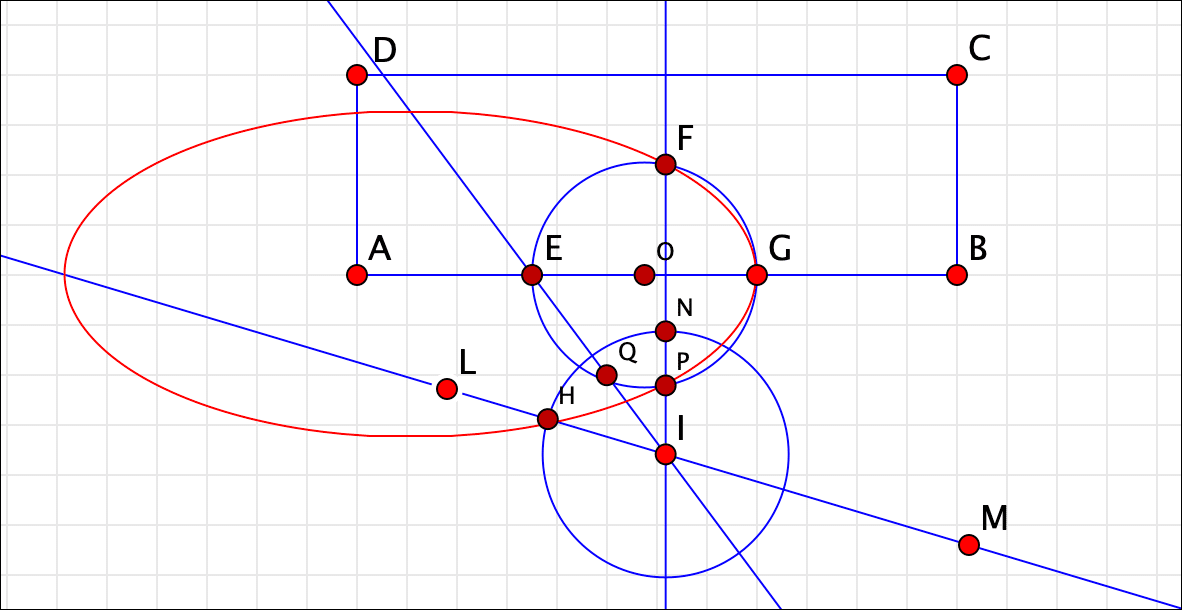
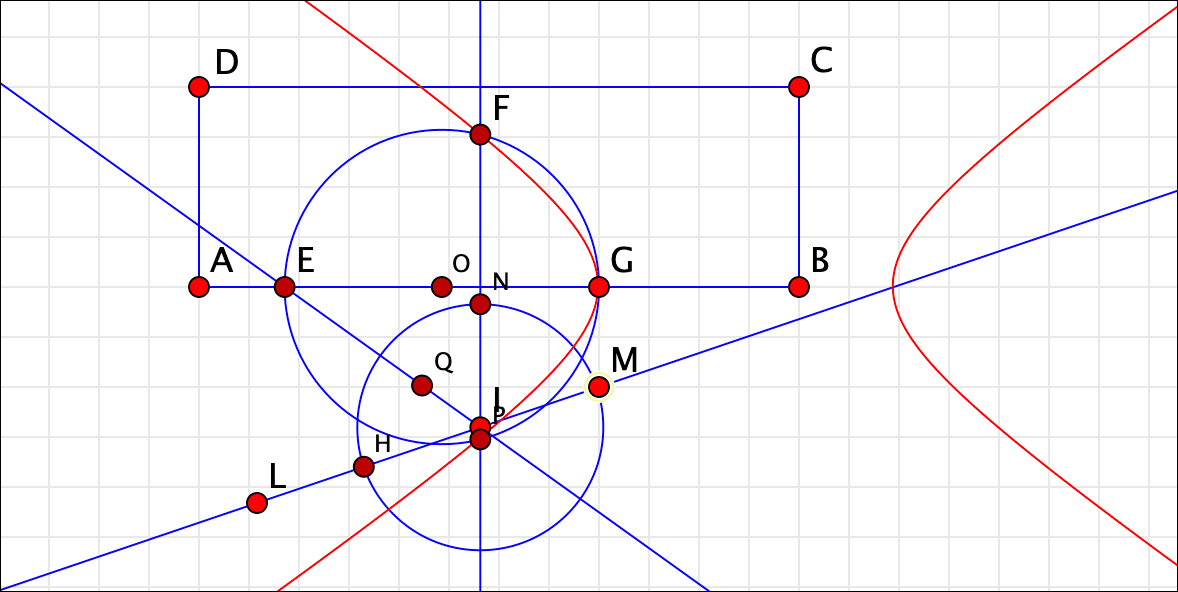
放物線の場合について,作図器を模したものを作りました。作図器と同様に,直線LMも可動にしたいのですが,棒の可動域の制限をつけることなどが面倒なので,放物線だけにしました。
← Cinderellaで数学・情報:記事一覧 に戻る
