
インドラの真珠:反復関数系
複素関数による写像(点や図を写すこと:map)の繰り返しを行います。
関数 f(z) があるとします。
最初の複素数 を z0 として、z1=f(z0) , z2=f(z1) , z3=f(z2), ・・・ と繰り返していきます。
リンク先を開くと「複素関数(3)」と同じような画面が出ます。水色の関数のボタンがない場合は再読み込みしてください。
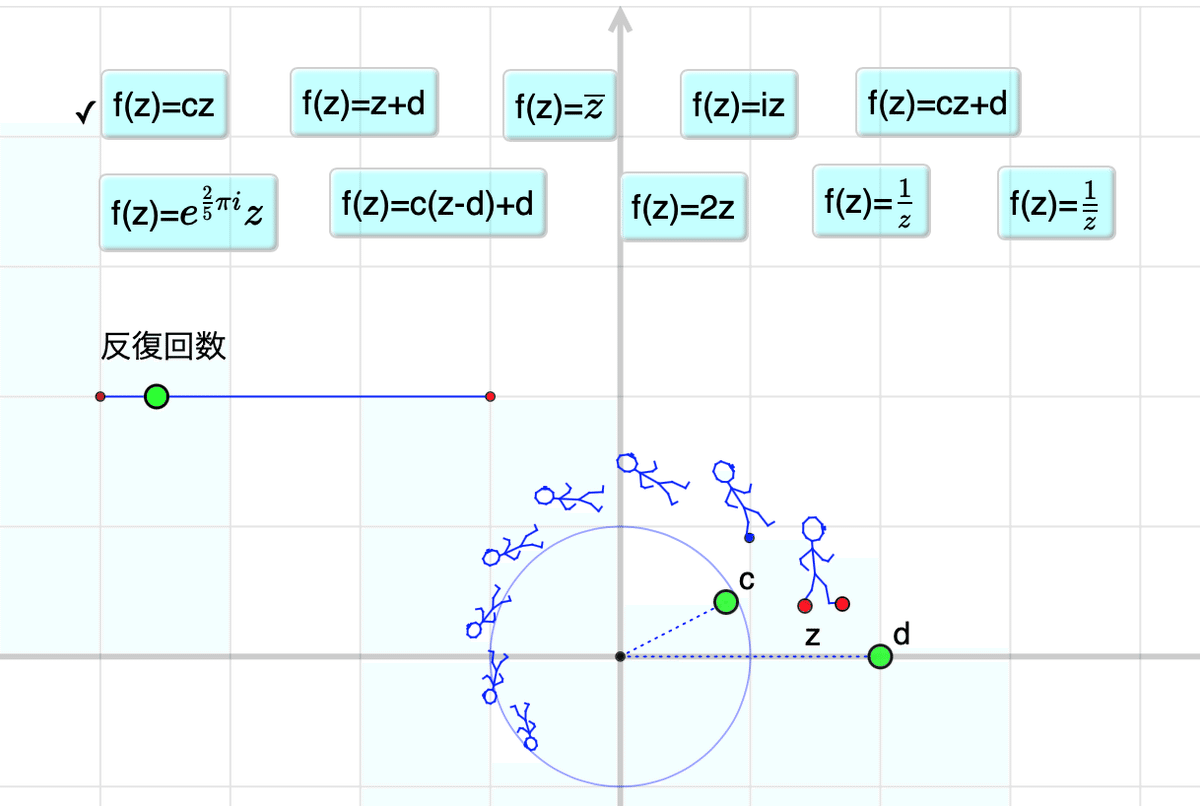
はじめの図は f(z)=cz という関数で、cは複素数です。絶対値が1より小さいので、回転とともに原点との距離が縮小します。これを繰り返していくと螺旋状に縮小していきます。この螺旋は対数螺旋です。
元のスティックラー博士の図は、「複素関数(3)」とは異なり足下の2つの点をドラッグすることで位置や大きさ,向きを変えることができます。反復回数はスライダで調節できます。
いろいろ試してみましょう。
=================
ここからあとは,「複素関数(3)」の続きで,反復関数系をCinderellaで作図する方法の説明です。複素関数(3)」で作ったものの一部を変えるだけです。
関数定義の次の2行を,次のように書き換えます。
repeat(4,
st=apply(st,s,apply(s,f(#)));
apply(st,s,draw(gauss(s_1),gauss(s_2)));
);
repeat(4, は4回繰り返す,という意味です。繰り返す内容は末尾の ); までです。
前と異なるのは,stmap が st となっていることです。繰り返すために,st を変えた結果をそのまま st に代入しています。
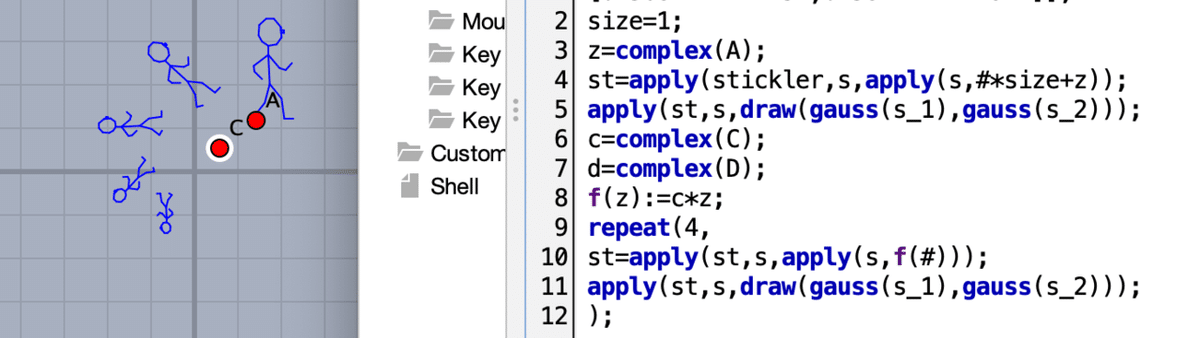
このままではちょっと操作しにくいので,スケールを変えます。下のツールの左から3番目「矩形領域を画面サイズに拡大」を選び,拡大する領域の左上から右下までマウスドラッグで指定します。マウスボタンを離せば全体が拡大されます。

失敗したら,一番上のツールの左から7番目,取り消しツールで戻せます。
拡大したら,「要素を動かす」ツールで選択モードに戻しておきましょう。
リピートの回数を増やしてみましょう。
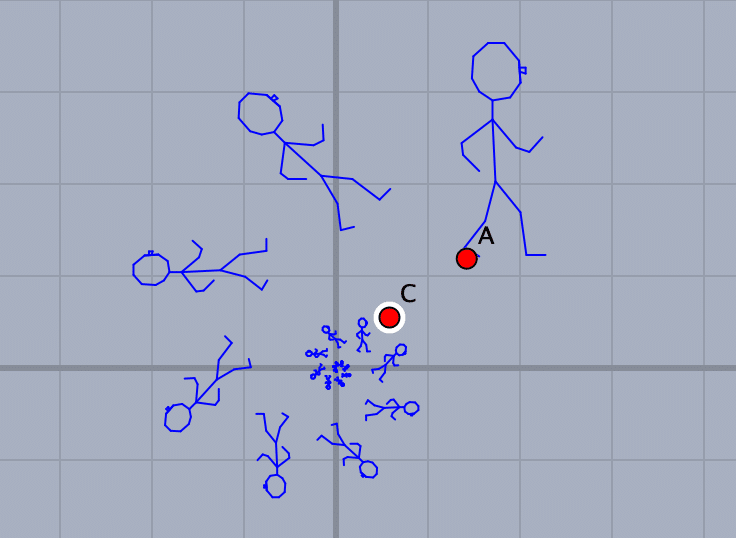
「複素関数(3)」と同様に,いろいろな関数やc,d の値を試してみましょう。
→ インドラの真珠:目次 に戻る
