
Cinderellaで数学:いろいろな曲線:マクローリンの円錐曲線作図器
「曲線の事典」(礒田正美他編著:共立出版 2009)に掲載されているものです。作図ツールを使った場合,他の円錐曲線作図器と異なり,ひとつの図で点の位置を変えるだけで,楕円・放物線・双曲線を描くことができます。
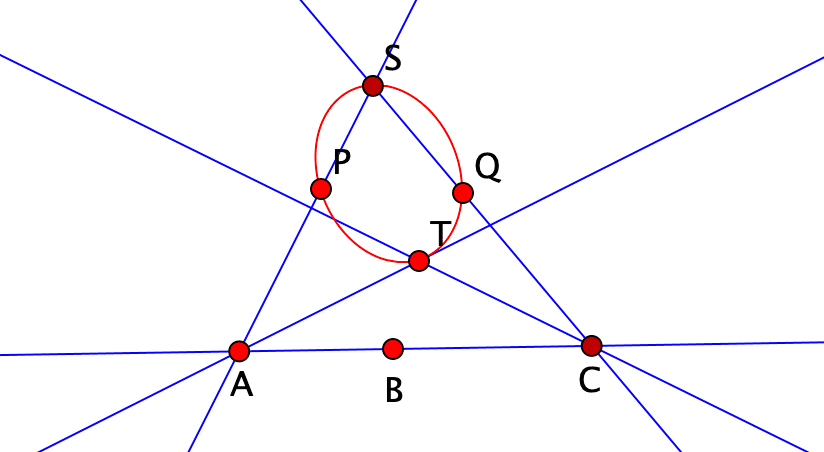
マクローリンの円錐曲線作図器は次のように作られる。平面上の固定点P,B,Q をそれぞれ通る直線 AS,SC,ACによって△ASC が与えられている。頂点A,Cはそれぞれ直線 AT,CT上を動く。このとき、第3の点Sは円錐曲線をかく(図は楕円の場合)。

この説明には補足が必要でしょう。そのために,Web上に載っている作図器の写真も見てみましょう。上の写真より少しわかりやすいでしょう。

「頂点A,Cはそれぞれ直線 AT,CT上を動く」となっていますが,作図器を見ると,両方が自由に動かせるわけではありません。点A(左の点)がTを通る直線上を動くと,Bを通る直線が動き,それによって,Cの位置が変わります。Aを字融点とするなら,Cは従属点になります。また,AはTを通る直線上を動くので,「Aは直線AT上を動く」というのは不正確な表現です。
以上が納得できたら,Cinderellaで作図します。
4つの点,P,Q,B,Tは固定点とはいえ,Cinderellaの作図ではインスペクタで固定点にする必要はありません。というより,自由点にしておかないと,3種の円錐曲線は描けません。まずこの4点をとります。順序は問いません。
点Tに相当するのがDだとします。Dを通る直線DE,DFを引き,DE上に点Gを取ります。
直線GAを引き,交点をHとします。直線BGとCHを引き,交点をとります。
軌跡ツールを選び,動かす点としてG,軌跡を描く点としてKを選べば楕円が描かれます。

背景を白にして,点EとFは非表示にし,点の名前を説明図のように変えたのが次の図です。
次の図は,手を加えて作図器を模したものです。(タイトル画面も)
ただし,このように棒(線分)で表すと楕円の作図器しか作れません。

これで円錐曲線が描かれる理由について,本では射影幾何学で説明しています。詳しくは本を参照してください。まとめとして次の3つが示されています。

図2.63の放物線は上下が逆ですが,要するに,4点P,Q,T,Bの位置関係によって3種の円錐曲線が描かれるということです。作図したものはそのままで,4点の位置関係を変えてみましょう。


円錐曲線は点Sの軌跡として描きましたが,図2.62〜2.64(再掲)を 見ると,5点を通る2次曲線であることがわかります。PBとCTの交点R,QBとATの交点Uを追加した5点です。

Cinderellaの作図ツールには「5点で決まる2次曲線」というツールがあるので,点R,Uを追加して,このツールで描画してみましょう。

HTMLに書き出してCindyJSで表示するとき,軌跡ツールで描いた軌跡は表示されませんが,「5点で決まる2次曲線」で描いた曲線なら表示されます。Web上で動かせるようにしたのが次のページです。
線分を棒にする方法は,「交叉平行四辺形を利用した円錐曲線作図器」のページで説明しています。
