
センター試験「情報関係基礎」2007年のブロック落としをCindyScriptで書く
センター試験「情報関係基礎」2007年の第3問は,ブロック落としゲームのプログラミングである。
まず,ルールの説明がある。マス目の中にいくつかのブロックが積み上げられている。ブロックには,整数が書かれた「数ブロック」と,「+」「−」「×」のいずれかが書かれた「演算ブロック」がある。次の手順で計算しながらブロックの置き換えや移動をおこなう。
手順1 計算は,最下段のみを対象とし,左から順に計算可能な組み合わせを調べる。計算可能な組み合わせは,三つのブロックで,「1」「+」「2」のように数ブロックの間に演算ブロックが一つある場合のみとし,「+」「2」「4」のような場合は計算しない。計算した後は,中央の演算ブロックをその結果が書かれた数ブロックで置き換え,左右の数ブロックを取り除く。この作業を右端まで繰り返し,手順2へ進む。
手順2 手順1のあと,取り除かれたブロックがある場合は,その上のすべてのブロックを1マス下に移動させ,手順3へ進む。
手順3 手順1で,一度も計算しなかった場合,ゲームは終わる。そうでなければ手順1へ戻る。
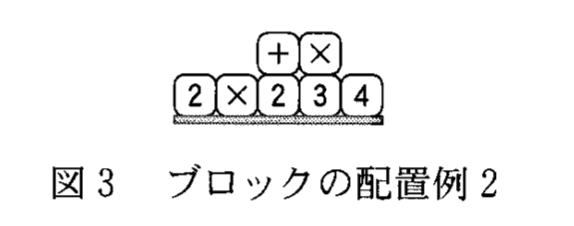
例とその説明が示されている。

手順を簡単に示すと
(A) 1+2が計算可能で結果は3になる。
(B) 「+」を「3」で置き換え,左右のブロックは取り除く。
(C) この状態では計算はできない。
(D),(E) 手順2に従い,「×」ブロックを下に落す。
(F),(G) 手順1に戻り,計算可能かどうか調べる。
(H)計算して置き換える。これで終了。
このルールを確かめるために,次の配置例で問題とし,さらに,その次の4パターンを調べさせる。ここが結構面倒な箇所だが,これによってアルゴリズムを確かめるわけだ。

次からプログラミング。ブロックの状態を4行8列の配列で表す。

まず,手順1をプログラムする。最下段のブロックの計算だ。

続いて,手順2。空欄になったブロックに上から落す。

最後が全体。

この中の kosuu と keisan の計算が示されていないので,次の図8の代入文をどこかに挿入してでき上がる。どこに挿入するかが設問だ。

さて,ゲームのルール(アルゴリズム)が正しく理解できれば,あとは,繰り返しと条件判断,配列への値の代入なので難しくはないのだが,実際にこれをプログラムして動かそうとすると問題が生じる。初期設定と表示の問題である。
まず,配列Tの初期状態や,最初のブロックの個数を数えるコードは問題の中にないので,作っておかなければならない。ブロックが数ブロックか演算ブロックかを判定するコードも必要だ。ブロックの表示は,配列をコンソールに表示するのではなく,図として示したい。
そこで,授業では,それらを準備したものを作っておき,生徒は問題の通りのコードを書けばよいようにしておく。穴埋めだけでなく,周辺の「もし・・ならば・・・を実行し・・・」の部分も書かせたい。どのくらい作り込んでおくかは,生徒の理解状況によるだろう。
また,この問題は非常に興味深く,次のようなパターンが作れる。
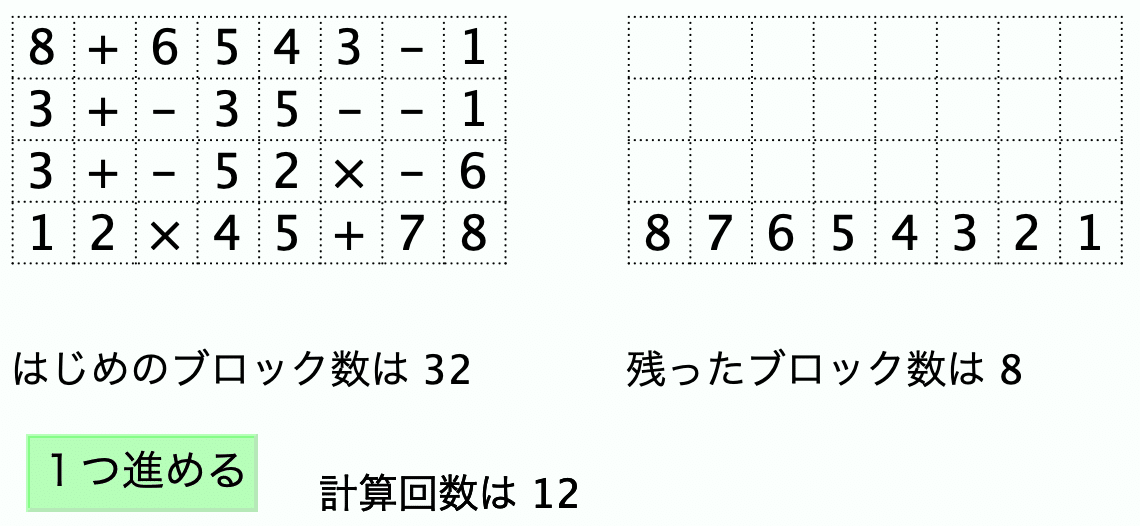
・最上段と最下段の数字を1から8まで逆順・正順に並べ,そのうち2つを
演算ブロックに変えた。
・初期状態で空のブロックがないようになっている。
・最終結果は最下段だけ残り,1から8まで逆順に並ぶ。
昨年,一昨年と,このようなパターンを作ってみよう,という課題を自由課題として授業後に出したところ,十数名が応募してきた。ちょっとした頭の体操である。中には驚くようなものがあった。
テキストは昨年,一昨年と,生徒のできぐあいをみて,少しずつ修正し,今年は次のようにしてみることにした。(授業はまだ)
図5の手続き1は calc() という関数にする。「図7 ゲーム全体の手続き」をみればわかる通り,関数化して呼びだす形だ。問題の通りに空欄になっている。
// 図5 計算を実行し,計算回数を返す
calc():=(
repeat( ,x,start->2, // 回数を入れる。キに相当
if(isinteger(T_(x-1)_1) // T[x-1,1]が数ブロック
& isop(T_x_1) // かつ T[x,1]が演算ブロック
& isinteger(T_(x+1)_1), // かつ T[x+1,1]が数ブロック
if(T_x_1== , // ク
T_x_1=T_(x-1)_1+T_(x+1)_1);
if(T_x_1=="*", // そうでなくて「×」ならば
T_x_1=T_(x-1)_1*T_(x+1)_1);
if(T_x_1=="-",
T_x_1=T_(x-1)_1-T_(x+1)_1);
T_(x-1)_1= ; T_( )_1=""; // ケ,コ
);
);
);図6の手続き2は drop() という関数にする。
// 図6 ブロックを下に落とす
drop():=(
repeat(8,x,
if(T_x_1=="", // サ
repeat(3,y,
T_x_y=; // シ
);
T_x_4="";
);
);
);図7の全体は next() という関数にし,「1つ進める」ボタンで呼ばれるようになっている。生徒が書く事柄はない。図8の kosuu と keisan の代入文は, calc() の中のどこかに挿入する。
このように,まずセンター試験の問題をそのままの形で解いた後,それをCindyScriptでコーディングするのだが,calc() と drop() のコードはテキストに書いて,それを打ち込むことになる。(コメント文は打ち込まなくてよい) 問題と同じ箇所は補充して書くことになるが,全体としてはたいした分量ではない。他の部分(初期設定など)はすでに作り込まれている。
これを実際に動かすための関数がどうなっているかも書いておこう。
// block が演算ブロック +,-,* かどうかを調べる
isop(block):=(
if(block=="+" % block=="-" % block=="*",true,false);
);
// 左下の座標をxとしてmatを表示
dispblock(x,mat):=(
regional(str);
repeat(5,s,draw([x+1,s],[x+9,s],color->[0,0,0],dashtype->3));
repeat(9,t,draw([x+t,1],[x+t,5],color->[0,0,0],dashtype->3));
repeat(4,y,
repeat(8,s,
if(mat_s_y=="*",str="×",str=mat_s_y);
drawtext([x+s+0.5,y+0.2],str,align->"mid",size->24);
);
);
drawtext([6,-3],"計算回数は "+keisan,size->20);
);このほか,配列 T の表現など,いくつかあるが,あまり問題になるところではないので略す。一番問題なのは,表示のためのコード(上のコードで dispblock() )だ。Cinderellaの描画面に表をつくり,リスト T の内容を表示している。
次は,これを Python で書いてみよう。
