インドラの真珠：Barnsleyのシダ

2022年3月17日 07:36

　反復関数系の有名な例に「バーンズリーのシダ」があります。シダの葉は、全体と部分が相似な自己相似形をしています。アフィン変換の反復関数系を用いて次のような図が描けます。CindyJSのギャラリーにあるものです。

赤い点をドラッグすると形を変えることができます。また，先端の点はアニメーションになっていて動いています。
点は12個あります。一つのアフィン変換は3つの点の対応で決められますので，ここでは４つのアフィン変換を使っていることになります。
タイトル画像はCindyJSではなくCinderellaで作成したものです。上記のリンク先をにあるものとは色合いなどが違っています。上記のリンク先のものは，CindyGLという描画エンジンも使っています。一方，タイトル画像のものではプログラムは書いていません。Cinderellaに備わっているツールだけで描いています。以下で，その作り方を説明しましょう。

　まず、編集メニューからインスペクタを開き、「表示方法の初期設定」で直線の表示方法を「端点で切る」（一番右）にしておきます。

線分を描くツールで、線分ABを引きます。次に、垂線を描くツールをクリックし、線分AB上でマウスボタンを押し、そのまま点Aまでドラッグします。

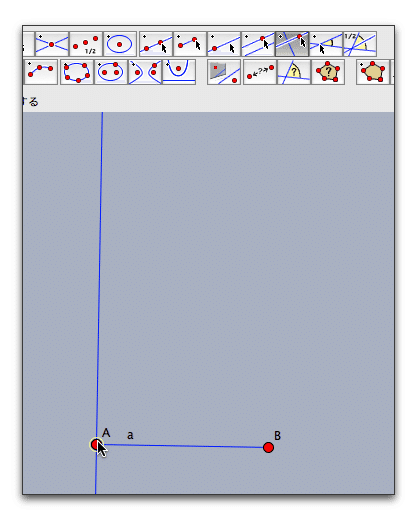
できた垂線上の適当なところでクリックして、さらに垂線を描きます。線上でマウスボタンを押して少し動かしてから離します。

AB上でマウスボタンを押し、Ｂまでドラッグして、Ｂを通る垂線を引きます。

「２つの直線の交点を求める」ツールをクリックし、Ｃから引かれている直線をクリックします。

すると，インスペクタで「端点を切る」にしておいた効果で，直線が線分に変わり，長方形ABDCができます。これが、アフィン変換の元になる３点A,B,Cからなる長方形になります。

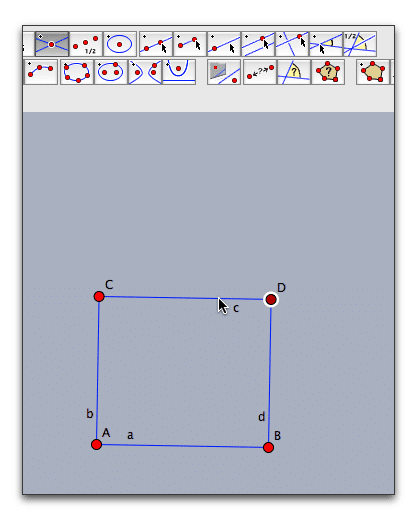
同じ要領で長方形を４つ追加します。
シダの葉の曲がり具合を示す長方形（次の図EFHG)
左の葉に関係する長方形（KLNM）
右の葉に関係する長方形（OPRQ）
茎を描く長方形（STVU）：中央に細目に
描く順序は問いません。長方形の頂点を描く順序も問いません。とにかく、全部で５つの長方形を描きます。
ただし、ある程度は次の図のような位置関係と大きさで描くのがよいでしょう。

　これで、アフィン変換を作るための図形ができました。実際には長方形の４つの頂点のうち、使うのは３つだけですので、必ずしも長方形である必要はありません。あとで示すような直角に折れ曲がった４組の線分でも結構です。
　では、アフィン変換を定義します。モードメニューの「変換」からアフィン変換を選び、まず、次の図のように３つの対応を指定します。順序は問いません。