
Cinderellaで数学:いろいろな曲線:ストロフォイド
「曲線の事典」(礒田正美他・共立出版2009)に掲載されている作図器によるストロフォイドを描きます。
ストロフォイドの定義
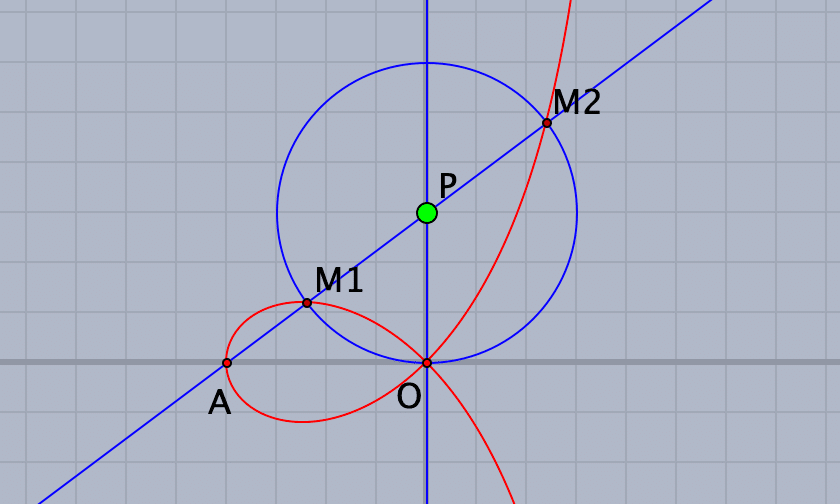
直線 s 上に固定点Oと動点P,直線 s 上にない点Aが与えられている。点Pが直線 s 上を動くとき,$${\rm{PM}_1=\rm{PM}_2=\rm{OP}}$$ をみたす直線上のAPの点$${\rm{M}_1,\rm{M}_2}$$ の軌跡をストロフォイド(葉形線)という。
簡単な作図なのでやってみましょう。直線 s をx軸にとるかy軸にとるか,どちらでも結構です。次の図は,y軸にとったものです。点の名前は作図後に定義に合わせて変えています。
ニュートンの作図器
ニュートンの作図器では,シッソイドとともにストロフォイドが描かれます。次の図は,シッソイドの作図器と同じものでストロフォイドを描いたものです。

次のページに作図器を模したものを載せました。
ケトレーの作図器
円柱に,半径Rの2つの球が内接している(それぞれの中心をO,O'とする)。円柱を2つの球に接する平面によって切断するときの切断平面と球の接点をそれぞれF,F’,点P,Qを切断図形として得られた楕円の頂点とする。ここで、3点O,O',Pを通る平面による円柱の切断面を考える。切断面は、図のように、平行な2直線 a,bと,この2直線に接する中心O,O'の円,および2点F、F'で接する直線PQによって構成される。2つの円が2直線 a,bによって区切られた横長の領域内を転がり,直線PQが2つの円に接しながら点Pを中心に回転するとき,2点F,F'はストロフォイドをかく。

「球」「円柱」とありますが,実際には写真のように円盤になっています。Web上の写真は次のページにあります。
したがって,右の図のように作図すればよいでしょう。Pを定点とし,Qを動点としてPQが共通接線になるような2つ円を描き,その接点の軌跡を描けばよいわけです。
① 平行線を3本引く
② 下の直線上の点と,上の直線上の点を通るように斜めの直線を引く。
下の点を定点,上の点を動点とする。
③ 下の直線との角の二等分線を引く。右と左の2本。
④ 中央の直線との交点を求める。
⑤ ④の交点を中心とし,上下の直線に接する円を描く。
⑥ 2つの円の中心から,斜めの直線に垂線を引き,交点を求める。

⑤の円ですが,図のHを背景のy軸上に持っていくと,角の二等分線が45度の角になるので中心が格子点にきます。スナップ機能を使えば半径をうまくとれます。あるいは,固定した半径の円を描いてもいいでしょう。
軌跡ツールで,動く点をH,軌跡を描く点をNまたはMとすればストロフォイドが描かれます。

