
インドラの真珠:ショットキー円
前節で、2つの円を用いてメビウス変換を定義しました。こんどは,これを2組作って反復関数系を定義します。これをショットキー円といいます。「ショットキー」は人の名前で,フリードリッヒ・ヘルマン・ショットキーは20世紀初めの数学者です。
リンク先を開くと次の画面になります。黒地に青の円で,少し見にくいですが,オリジナルに合わせました。
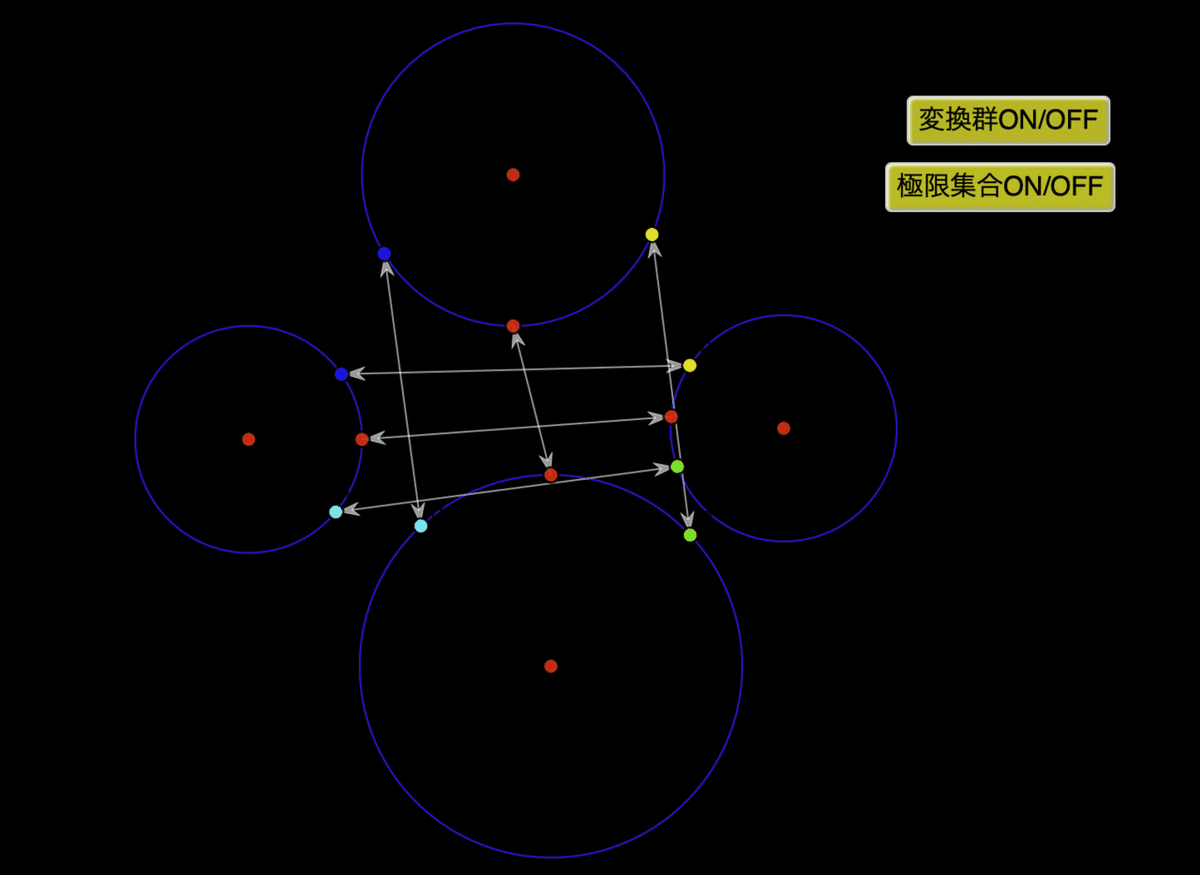
上下の2つの円でメビウス変換とその逆変換を定義しています。そのために使っている3組の点の対応が矢印で示されています。また、左右の2つの円でも同様にメビウス変換とその逆変換を定義しています。
これらの、全部で4つの変換ならなる変換群や反復関数系を定義しますと、その極限集合が描かれます。「変換群ON/OFF」ボタンを押してみましょう。

小さな円は、もとの円をメビウス変換または逆変換で何回か写してできた像です。「変換群」をOFFにして「極限集合」をONにしてみましょう。
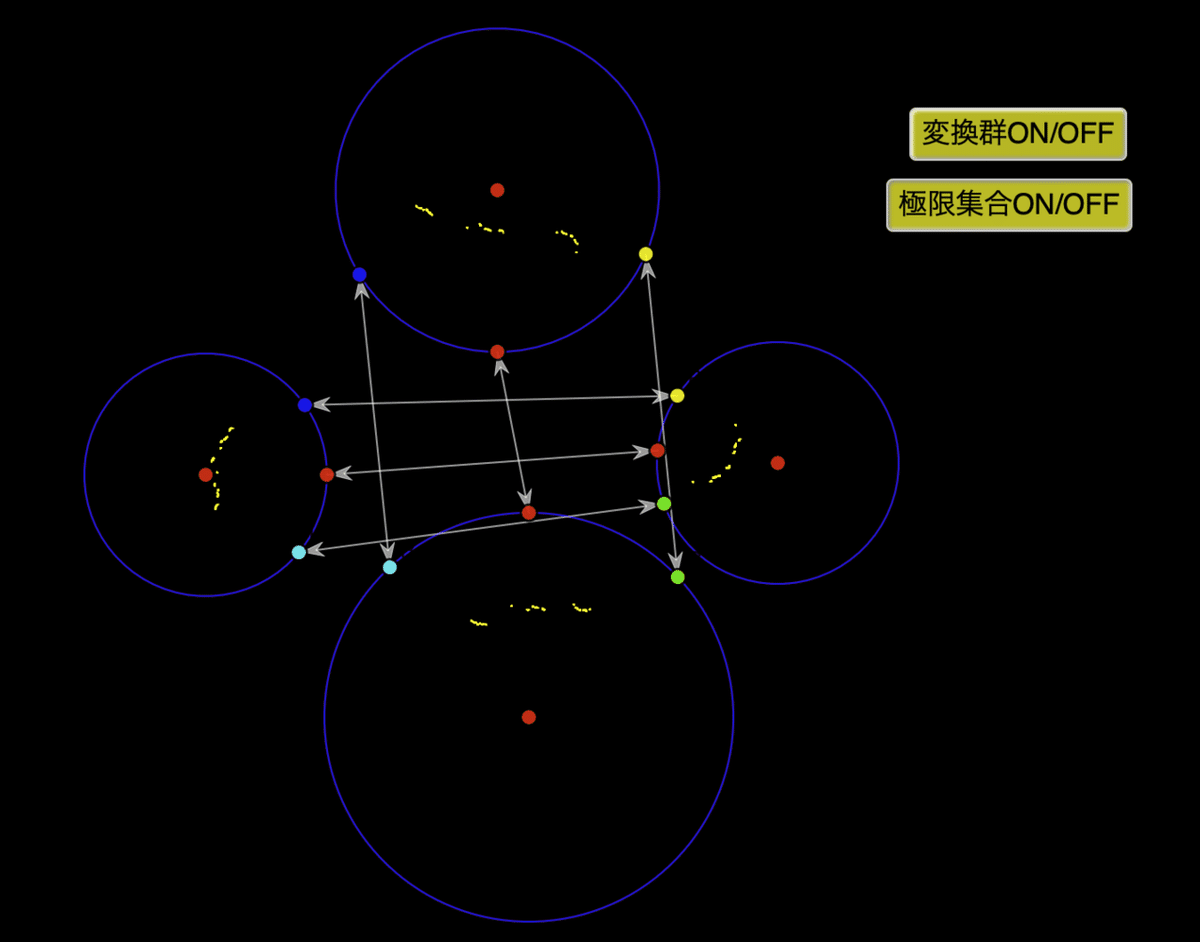
メビウス変換を定義する点の位置や,円の位置,大きさを変えてみましょう。
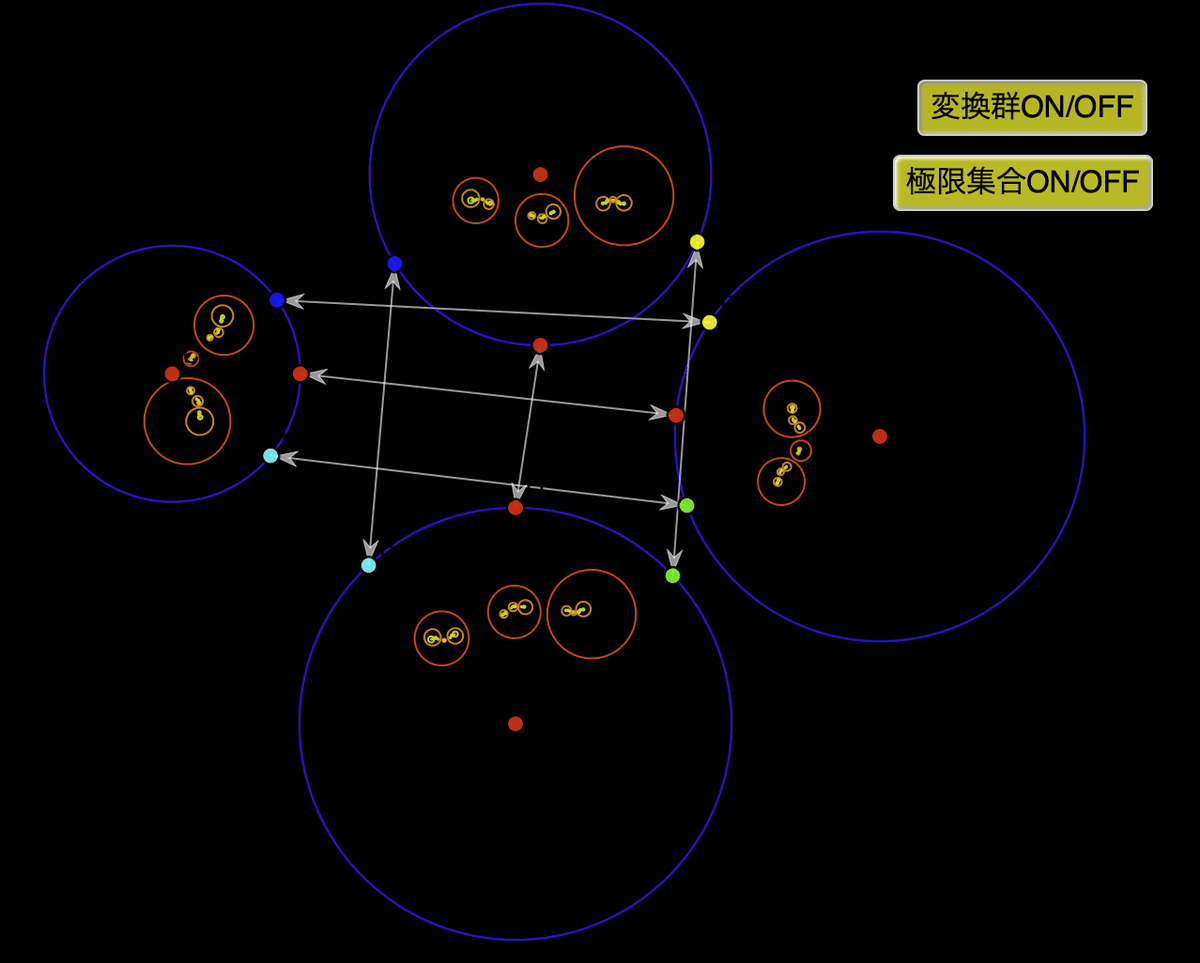
前の節でもやったように、これらの円が接するようにしたらどうなるでしょう。さらに、その接点が、メビウス変換を定義している点に一致するようにすると?
次の図でだいぶ近づけてみました。

さて,何がどうなるか,は見てきましたが,なぜそうなるかはよくわからない人が多いでしょう。次の節では,ステップを追って,詳しく見ていきます。
-----------------
Web上で動かすためにはプログラムを書いてCindyJSでHTMLにしていますが,Web上で動かなくてよいならCindyScriptを使わず,Cinderellaの作図機能だけで描くことができます。この場合は,点を動かすときの反応もよくなります。ここからはその手順を示しますので最初から作ってみましょう。
まず、「半径つき円を加える」ツールで上下左右、4つの円を作り、それぞれの円周上に3つずつ点を取ります。
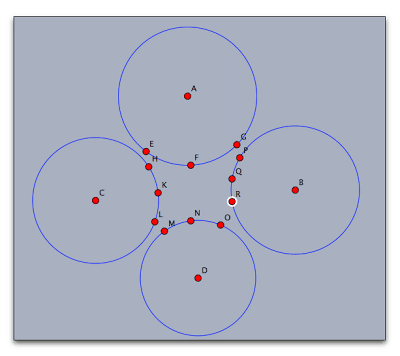
次に、モードメニューから「変換」「メビウス変換」を選び、ガイドに従って上下の円周上の3つの点を対応させます。

左右の円についても同様に3つの点を対応させます。

モードメニューから「変換」「逆変換」を選び、右上にできている変換のアイコンを順にクリックします。これで、2つのメビウス変換とその逆変換が定義できます。右上に4つのアイコンができます。

次に、円をいくつか写します。
まず、動かすモード(選択モード)にして上の円を選び(円周をクリック)、1つ目のメビウス変換のアイコンをクリックします。円の中に小さな円ができます。続けてクリックするとさらにその像ができます。5個ほど作ってみましょう。(円はどんどん小さくなりますので、単に5回ほどクリックすればよいです。

次に、下の円を選び、1つ目のメビウス変換の逆変換のアイコンを5回ほどクリックします。
さらに、右の円を選び、2つ目のメビウス変換のアイコンを5回ほどクリックします。
最後に、左の円を選び、2つ目のメビウス変換の逆変換のアイコンを5回ほどクリックします。
これで、4つの円の中にそれらの像ができます。
次に、変換群を定義します。4つの変換のアイコンをすべて選択します。シフトキーを押しながら順にクリックします。モードメニューから「特別」「変換群」を選びます。「TG0」というアイコンができます。
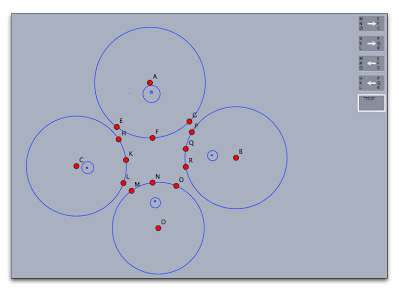
左側の円を選び、変換群のアイコンをクリックします。

上の円を選び、変換群のアイコンをクリックします。
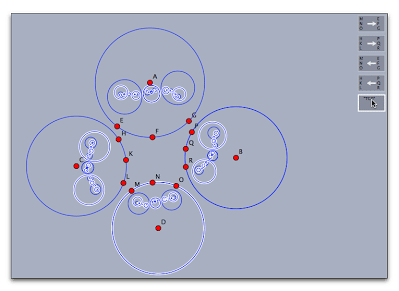
かなりたくさんの円ができました。小さな円がチェーン上に並んでいます。
最後に反復関数系を定義します。
4つの変換のアイコンをすべて選択して、モードメニューから「特別」「特別/反復関数系」を選びます。

これでできあがりです。
あとは、インスペクタで適当に色を変えて楽しみましょう。
→次節:ショットキー・ダンス
→インドラの真珠:目次 に戻る
