Cinderellaでカオスを描く:鳥の翼

2022年5月17日 14:53

「カオスＣＧコレクション」（川上博著：サイエンス社：以下「この本」）のはじめに，例1.2 として出ている鳥の翼（この本では「羽根」）。「Cinderellaでカオスを描く：関数の反復」と同じ手法で，関数を変えたものです。併記してみましょう。

前回は　　$${x_1=y_0+0.2x_0+\dfrac{5x_0}{1+x_0^2}}$$
　　　　　$${y_1=-x_0}$$

今度は　　$${x_1=y_0-0.97x_0+\dfrac{5}{1+x_0^2}-5}$$
　　　　　$${y_1=-0.995x_0}$$

分数の分子に$${x_0}$$ があるかないかの違いです。$${y_1}$$ の$${x_0}$$ の係数は同じ -1 にしても同じような鳥の翼ができます。
これについて，

特徴は，羽根状図形の近くに，初期値をどのように選んでも最終的にはこの図形に収束し，得られる図形は同じものとなる。

と書かれています。（5ページ）
掲載されているのは次の図です。（同 5ページ）

では，まずこれを描き，次に，係数を変えたり初期値を変えたりしてみましょう。着色もします。着色は，１万点ごとではなく，全体を256段階に分けた256色とします。「関数の反復」のときと同様，アニメーションで次第に増えていきます。初期値は$${(3,0)}$$です。

式は　$${x_{n+1}=a y_n-b x_n+\dfrac{c}{1+x_n^2}-d}$$
　　　$${y_{n+1}=-e x_n}$$
として，５つの係数$${a,b,c,d,e}$$ を可変とします。添え字は漸化式なので$${n,n+1}$$ としました。
リンク先を開くと，1000個の点から始まります。下方にあるスライダでそれぞれ係数を変更できます。

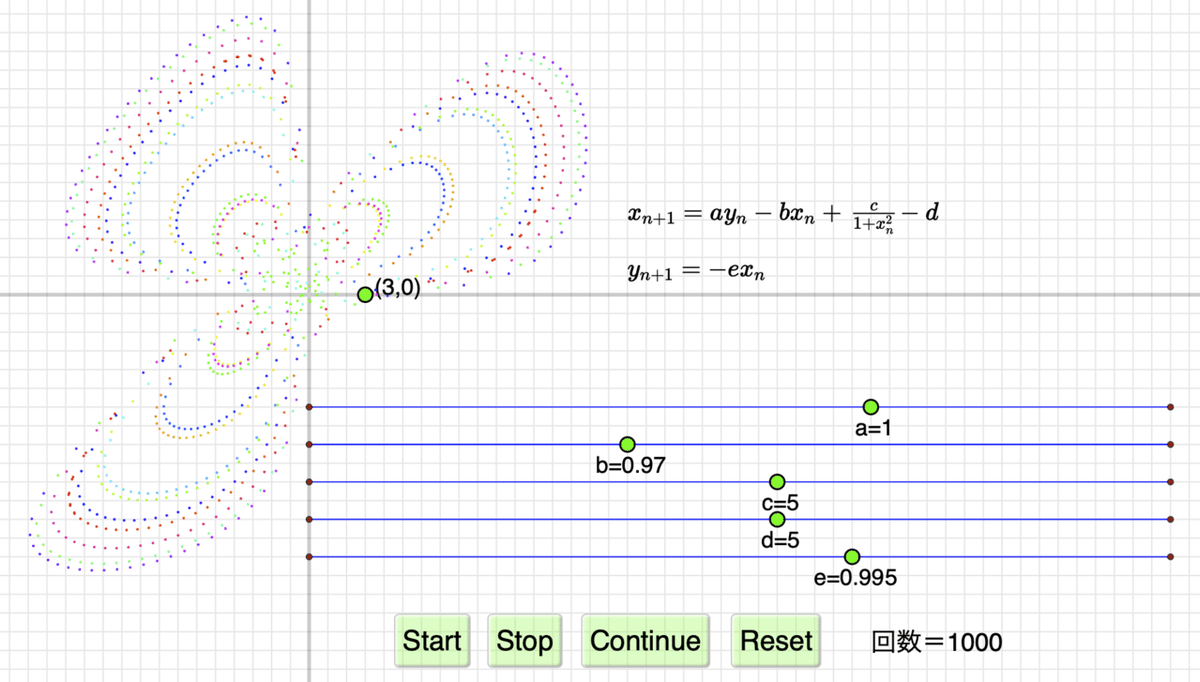
Start ボタンでアニメーションが始まります。Stopで停止，Continue で継続できます。図は次のように変化していきます。

「約」となっているのは，ぴったり止めるのがなかなか難しいからです。
図がだんだん緻密になっていきますが，羽根の輪郭は崩れません。すべての点がこの輪郭の中に入るのです。この本に「この図形に収束し」と書かれているのはこういうことでしょう。「初期値をどのように選んでも」については，このあと検証します。
　なお，向きが違って見えるのは，プロットの仕方が異なるためです。この本のプログラムだと，$${(x,y)}$$ をそのままプロットするのでなく，$${(x+y,x-y)}$$ としています。また，縦横比も４：７にスケーリングしています。筆者が作った方は$${(x,y)}$$ をそのままプロットしています。
　面白いのは，係数を変えたときの変化が必ずしも連続的ではないということです。たとえば，係数$${b}$$ を変えて少しずつ大きくしたとき，初期値の$${0.95}$$ 付近では羽根の幅が少しずつ変わっていくのですが$${b=0.99}$$ を超えたあたりで急に形が崩れます。

ところがそのあと，$${b=1.05}$$ を超えたあたりで再び凝縮（収束）します。
他の係数についても，いろいろな変化が見られます。次の図は羽根を広げた鷹のように見えます。

　では，次に「初期値をどのように選んでも」について実験しましょう。１０万点だと反応が鈍くなるのでおよそ５万点でやってみました。
一度 Reset して，まず5000点付近で Stop し，初期値の緑の点をドラッグします。点のつき方，色のつき方が違いますが（つまり，点が打たれる場所，順番が異なる）輪郭はほぼ同じです。