
プログラミング:円周上で正方形を転がす
プログラミング:正方形を回転する に続いて,円周上で転がしてみた。これが結構難航した。一時は断念したくらい。仕様を変更してなんとかできたのがこれ。
今回は,これの開発記。題材としては小・中学校のレベルだが,実現には高校3年生で学ぶ数学の内容が入っている。結構読むのはしんどいと思うので,適当に流し読みされてよい。
---------------------------------
1辺の長さがaの正方形を回転させて,着目した頂点の軌跡を図示する。
直線上と,正三角形上はやった。いずれも軌跡は半径a または ルート2・a の弧になるので,その始点と終点の位置がわかればよい。図を描いてみれば簡単にわかることなので,軌跡を描くのはたいして難しい問題ではない。正方形が難しそうだが,これは後述。

次に,円周上を転がる場合を考えた。
図示するのは正方形と軌跡なので,直線上の時と同様,それぞれを関数化することを初めから考える。しかし,決定的に違うことがある。それは,円周上を転がるとき,辺が円周上にあるときとそうでないときがあるのだが,辺が円周上にあるときは接点の位置が変わっていくことだ。直線上のときのように,パタッと辺が直線上に来たら次はまた頂点を中心に回転,というわけではない。
まず,どの状態から始めるかを決めておく。「円の上に正方形が乗っている」というイメージだと,滑り落ちないために,真上にある場合を考えるのがなんとなく自然だ。もちろん平面上に置いたものを真上から見ていると思えばその必要はない。

これを転がすと,はじめは辺が円周上にある。(辺と円が接している)

辺の半分だけ進むと,辺は円周上になく,1点だけが円周上にあるままで回転する。
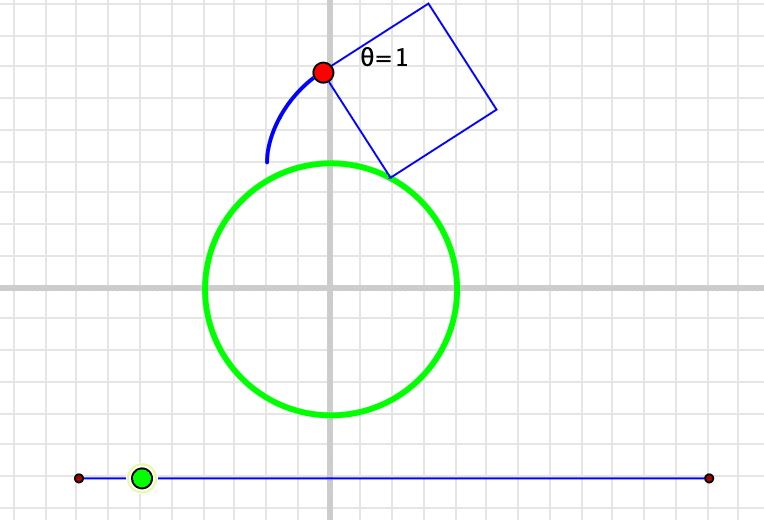
そのあとはまた辺が円周上にあり,そのあとは・・・・ と繰り返せばよい。(プログラミング的思考)
しかし,着目している点の位置が変わるので,話はそう単純ではない。(分析力)
軌跡も一見すると弧に見えるが,辺が円周上にあるときは中心がずれていくので円の一部としての弧ではない。1点だけが円周上にあるままで回転するときは円の一部としての弧だが,その始点と終点の位置を決めるのはこれまた簡単ではない。(分析力)したがって,直線上の時のように「plot 関数で弧を描く」のでは描けない。
初めは,正方形の1辺の長さの4倍が円周の長さになれば,ちょうど1周で戻ってくるのできれいに描けると思ったのだが,やってみてすぐにつまづいた。半径が無理数になり,転がり方が変わる境界点のところがぴったり合わないのだ。誤差の問題とは思うのだが,ひとまず解決できないので断念。半径を正方形の1辺と同じにした。こうすると,1辺の長さの弧に対応する角が整数になるので少し処理しやすくなる。実際には90度の回転角が弧度法で2分のπなのでいつもぴったりというわけではないのだが。(弧度法についての数学的知識とコンピュータの誤差についての知識)
これで初期の設計はできたことになる。あとは,書いていくだけだが,少しずつ状況が変わるので,まずは一つ一つ確かめながら書いていく。直線上のときと同様,正方形を描く部分と,軌跡を描く部分は関数化する。
まず,動き始めを考える。辺の半分の長さ r/2 が円周に接しながら動いていく。

半径r,弧の長さr/2に対する中心角は 1/2=0.5 なので(弧度法を使った中心角と弧の長さの関係:知識),スライダで得られる値を角を表す theta とすると,theta<0.5 の範囲だ。
次に,辺が円周上から離れて1点だけが円周上にある状態で90°回転する。(π/2=90° 回転するとふたたび辺と円が接する)その範囲は 0.5から 0.5+π/2 までだ。この間を描くプログラムを書いてみよう。初めの,「辺の半分が円に接している間」を第1区画,ここを第2区画とする。

// 第2区画
if(0.5<theta & theta<=0.5+pi/2,
th = theta-0.5; // この区画に来てから動いた角
locus1(0.5); // 第1区画の軌跡を描く
locus2(th); // この区画の軌跡を th まで描く
p1 = r*[cos(pi/2-0.5),sin(pi/2-0.5)]; // 正方形の1辺の右端は円周上の点
p2 = rotatepoint(p1,pi/2-th,4); // 正方形の1辺の左端を求める関数
v = (p2-p1)/|p2-p1|; // 正方形の向きを表す単位ベクトル
P.xy = drawsquare(2,p1,v,true); // 正方形を描く
);
ここで使っている locus2 は次のようになっている。
locus2(th):=(
p = r*[cos(pi/2-0.5),sin(pi/2-0.5)]; // 正方形の頂点が乗っている円周上の点
p1 = rotatepoint(p,pi/2,4); // :正方形の1辺の左端:軌跡の始点
plist=[p1]; // 軌跡をプロットする点のリスト
repeat(100,t, // th まで,100に分割してプロットする点を取る
k = pi/2-th*t/100;
p2 = rotatepoint(p,k,4);
plist = append(plist,p2); // リストに追加
);
connect(plist,size->2); // 点を結ぶ
);
はじめのp は,点の座標であると同時に,原点を始点とするベクトルを表す。このベクトルの終点から,これを pi/2 だけ回転して長さを4にしたベクトルを加えた終点をp1とする。その計算が rotatepoint() だ。なの,この 4 は r と同じだから r でもよい。
このあと,さらに転がった第4区画では,2行目の p の式にある角が変わるのだが,ひとまず,同じようなものを第4区画でも書いて動作を確かめる。あとでここを関数化するときに,位置によって変わるものを引数にすればよいだろう。
この中で面倒だったのが,軌跡の始点を求めることだ。
はじめは上のようにその都度計算式を書いていたが,「一つ前の軌跡の終点を始点にする」ことを思いついた。そこで,この関数で,戻り値としてプロット点のリストの最後の値を戻すようにした。すると,次のプロット関数でこの戻り値を引数にいれれば,その都度計算する必要はなくなる。
(関数の「引数」「戻り値」を使ったテクニック:プログラミング的思考)
ここで,与えられた線分ABを1辺とする正方形を描く方法を説明しておこう。「垂線を立てて・・」といった幾何的方法は使わない。「垂直な直線の方程式は」という,図形の方程式も使わない。
複素数を使って点AをBの周りに90度回転した点と,BをAの周りに-90度回転した点を作って結べばよいのだ。

z1 = complex(A); // 点Aの座標を複素数に変換
z2 = complex(B);
z4 = z1+(z2-z1)*(-i);
z3 = z2+(z1-z2)*i;
p1 = gauss(z1); // 複素数を座標に変換
p2 = gauss(z2);
p3 = gauss(z3);
p4 = gauss(z4);
drawpoly([p1,p2,p3,p4]); // 4点を結んだ多角形を描く
ただし,これは,高校の数学Ⅲで学ぶ知識(複素数平面)だ。知らなければ結構大変なプログラムになる。もちろん行列を使ってもよいが,今は大学生になるまで行列は学ばない。
「プログラミング的思考」だけではどうにもならない。中学生では無理。高校生で複素数平面を学んだ生徒にはちょうどよい題材だ。(実際に授業で扱っている)
一周するのに13ステップかかった。全部で500行くらいになった。できあがったところで,同じような処理をしているところを関数化していく。あとのためにコメント文も入れて210行ほどになった。
かくして,冒頭のように動かせるものができた。
もちろん,すんなりできたわけではない。計算ミス,かんちがい。予期しない結果が出るたびに修正だ。(コーディング技術)
====================
これを作っていて思ったことがある。上の文の中に「プログラミング的思考」とか「知識」とか書いた。このアプリケーションを作るときに,「プログラミング的思考」がどのくらい必要か。ご覧の通り,わずかなものだろう。
カレーを作るときの手順を考えれば,おいしいカレーができるか? 肉と野菜をどの大きさに切る?どの順に炒める? それを「手順化」すればカレーはできるのか? その手順化のためには,たまねぎとじゃがいもでは火の通り方が違う,という「知識」が必要ではないか。
必要なのは知識と,問題の分析力だ。数学の問題だから数学の知識が必要になる。題材は小学生でも考えられることだが,解決には高校生の数学が必要だ。
高校情報Ⅰの学習指導要領(解説)には,「プログラミング言語ごとの固有の知識の習得が目的とならないように配慮する。」という文言がある。あたりまえだ。このようなアプリケーションを作るとき,そんなものは「手段」であって「目的」ではありえない。しかし,その手段を習得しなければコードは書けず,何も作れない。
学年末試験が近づいてきた。2学期末からやってきたプログラミング。はたして,どのくらいの成果があったと判定されるだろうか。
