Cinderellaで数学:いろいろな曲線:コルノイド
「曲線の事典」(礒田正美他編著・共立出版)に掲載のものですが,「アーネシの魔女」と同じくギャラリー扱いで,作図器はありません。
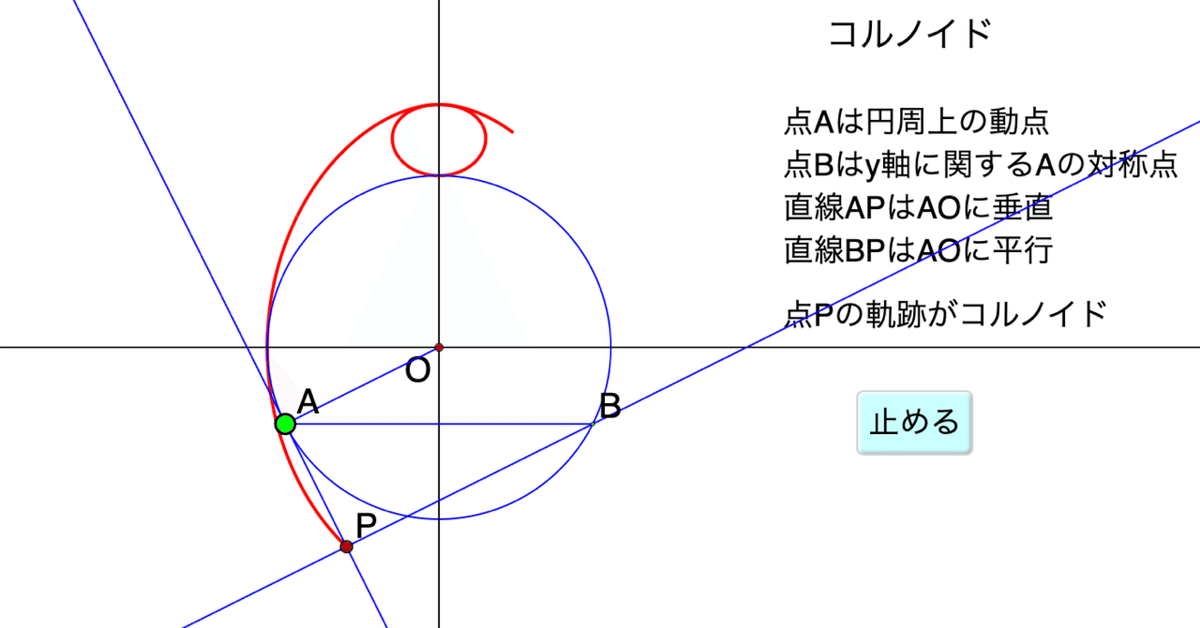
点Aは,点Oを中心,半径rの円周上を動くことができる。点Oを通る直線に関して,点Aと対称な点をBとする。点Aを通り直線 OAに垂直な直線と,点Bを通り直線 OAに平行な直線との交点をPとするとき、点はコルノイド(Cornoid)と呼ばれる曲線をかく。
この曲線は、Alberto Sanchez による著書“LaCornoide”(1895) の中で作図法が紹介されている。
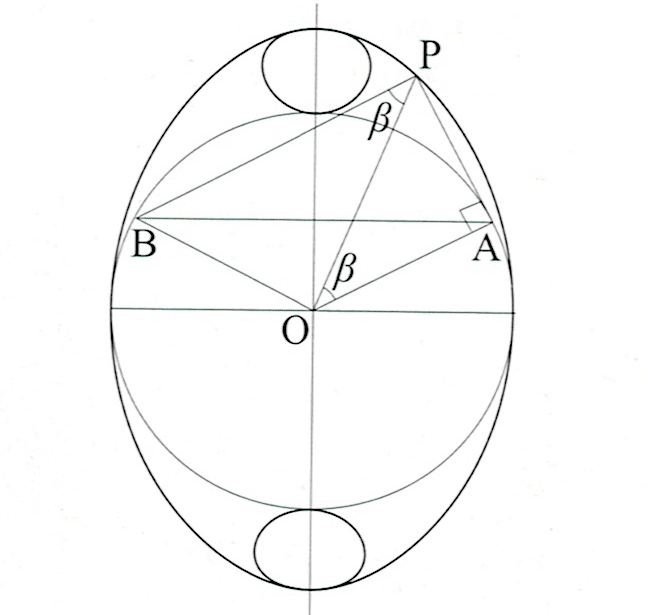
「Alberto Sanchezによる作図法」は書かれていないのでわかりませんが,コルノイド原典 【Elizondo-Ramirez 1995]の図があります。
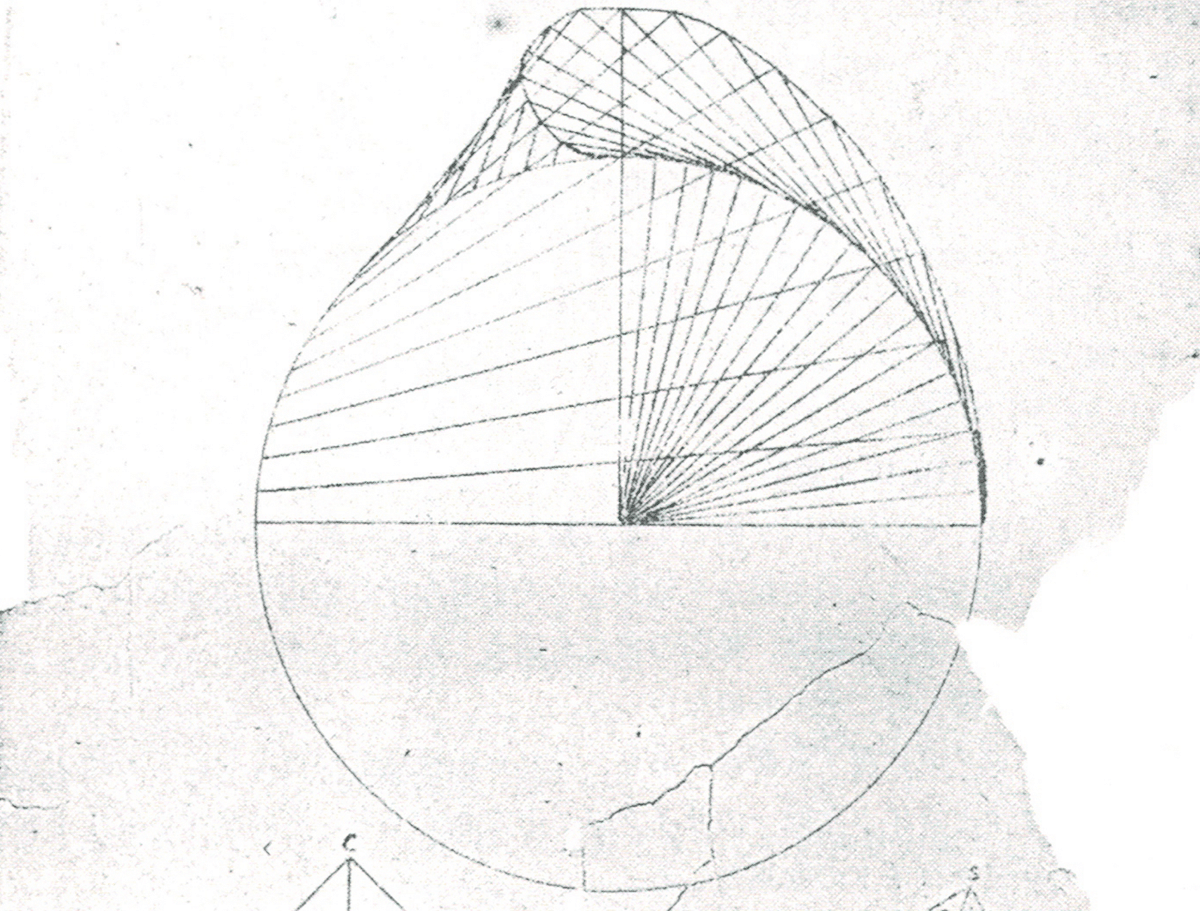
0から90°までいくつもの線を引いて点Pを滑らかにつないだもので,作図器のような作図法ではありません。
図は簡単なのでCinderellaで描いてみましょう。どのように描いてもよいとおもいます。たとえば,
① 線分ABを作図し中点Cをとって円を描く(上の図のABとは異なります)
② 円上に点を取り,ABに平行な直線を引いて円との交点を取る(D,E)
③ C,Dを線分で結び,Dを通る垂線と,Eを通る平行線を引き交点をとる。
④ 軌跡ツールを選び,動かす点としてD,軌跡を描く点としてFを選ぶ。
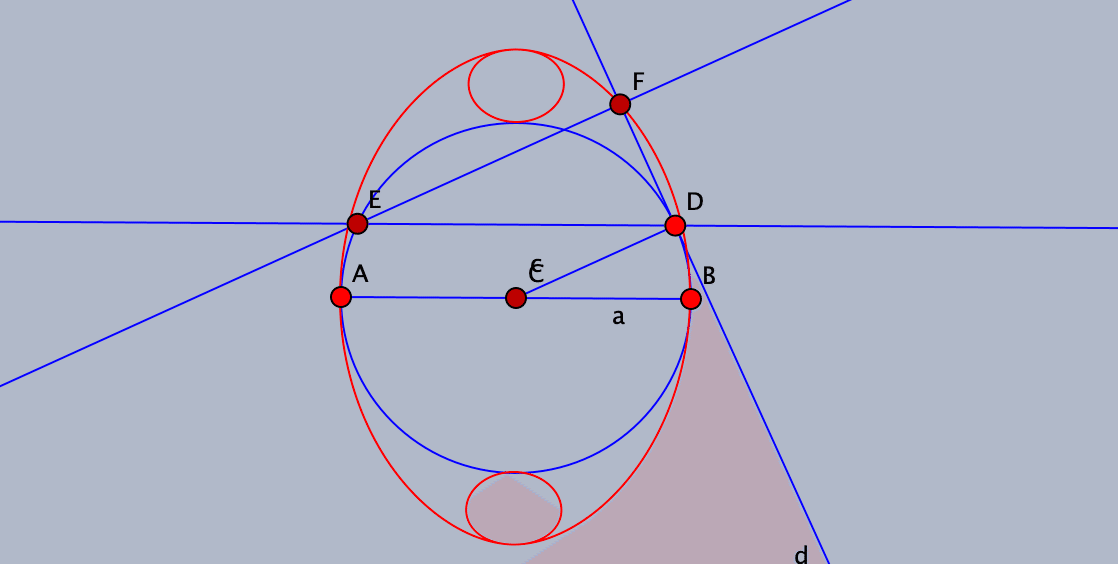
作図は簡単なのですが,興味を引くのは上下にあるこぶのような楕円形のものですね。90°までは,コルノイド原典の図でだいたいわかりますが,その先はどうでしょう。点Dをドラッグして動きを見てみましょう。
なかなか面白い動きをするでしょう。これをアニメーションで描けるとよいですね。また,HTMLに書き出してWeb上に載せるとすると,軌跡ツールで描いた軌跡は表示されませんので,CindyScriptで曲線を描くことになります。したがって,方程式が必要です。ちょっと計算してみましょう。
円の中心を座標平面の原点とし,両軸も描いて,点の名前も本の説明図と同様にしました。点Aの位置を表す角を$${\theta}$$,Aの座標を $${p,q}$$とします。
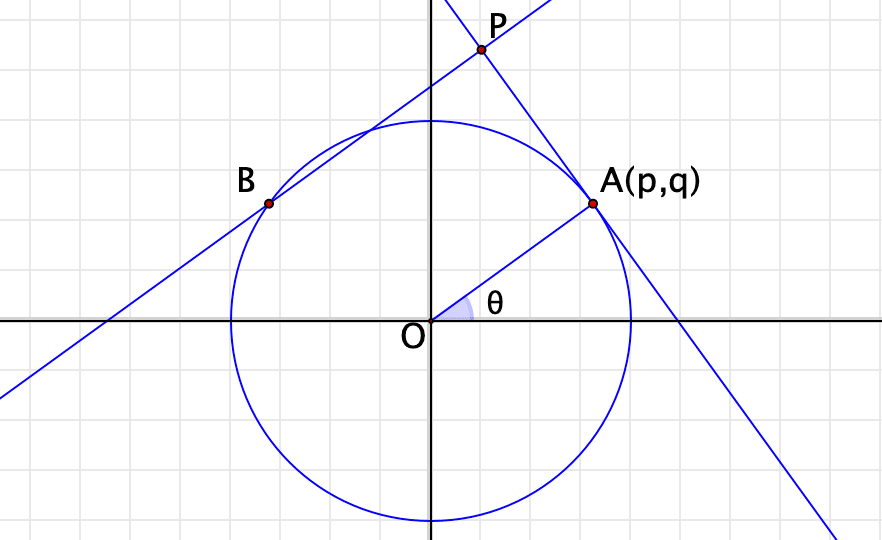
Bの座標は $${-p,q}$$なので,
直線APの方程式は $${y-q=-\dfrac{1}{\tan \theta}(x-p}$$
直線BPの方程式は $${y-q=\tan \theta(x+p}$$
となります。連立方程式を解いて,円の半径を $${r}$$ とし,$${p=\cos \theta,q=\sin \theta}$$ を代入すると,Pの座標は
$${r \cos \theta \cos 2\theta}$$,$${y=r\sin \theta(\cos 2\theta+2}$$
となります。これが軌跡の媒介変数表示となります。
Drawスロットに
r = C0.radius;
f(t):=[r*cos(t)*cos(2*t),r*sin(t)*(cos(2*t)+2)];
plot(f(#), stop -> 2*pi, steps -> 500, color -> [1,0,0], size -> 2);と書いて実行し,コルノイドが描かれればOKです。
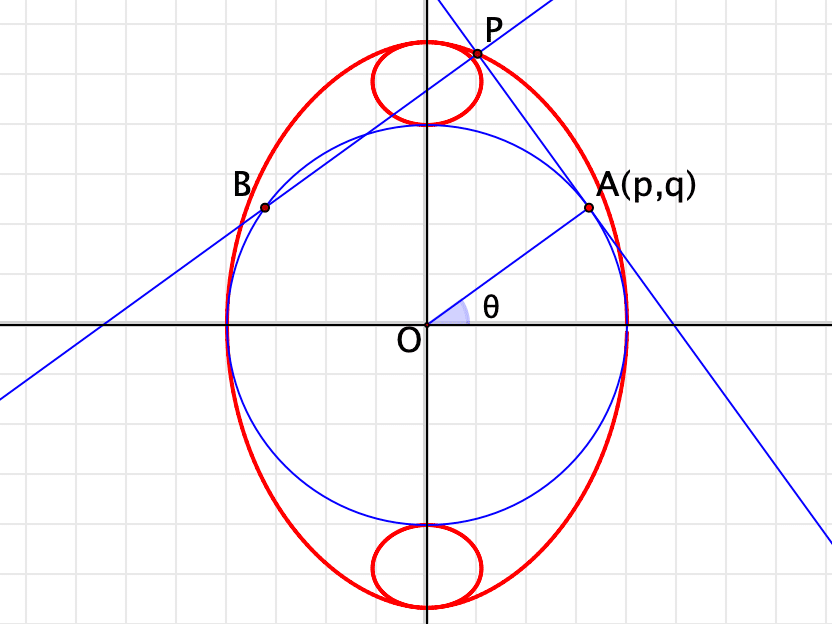
アニメーションにするには,内部時計を用いて時刻を取得し,それをそのまま Aの角として描画範囲を指定して描きます。
Initialization スロットに t = 0;
Simulation Start スロットに resetclock();
Timer Tick スロットに t = seconds();
を書き,Drawスロットを少し修正します。Aの座標を時刻 t で表し,plot の範囲を t までにします。
r = C0.radius;
f(t):=[r*cos(t)*cos(2*t),r*sin(t)*(cos(2*t)+2)];
A.xy = r*[cos(t),sin(t)];
plot(f(#), stop -> t, steps -> 500, color -> [1,0,0], size -> 2);左下にコントローラが出るのでプレイボタンを押すと,点Aが円周上を回転していくにつれて軌跡が描かれていきます。
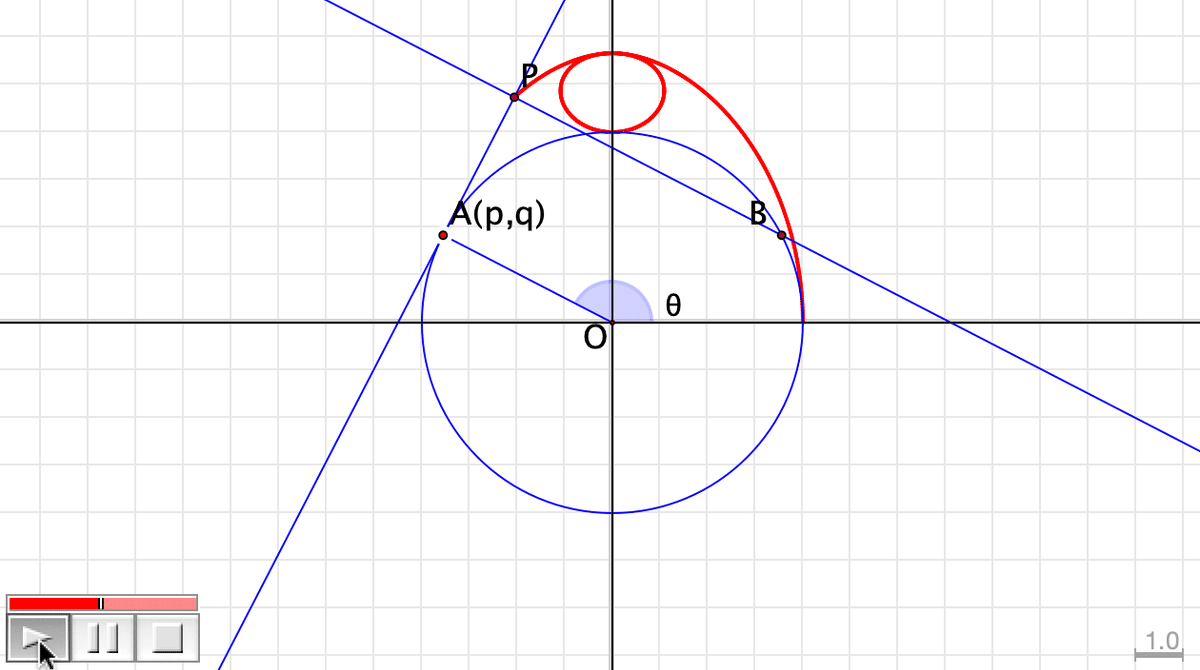
ボタンを作って使いやすくしたものをWeb上に載せました。
