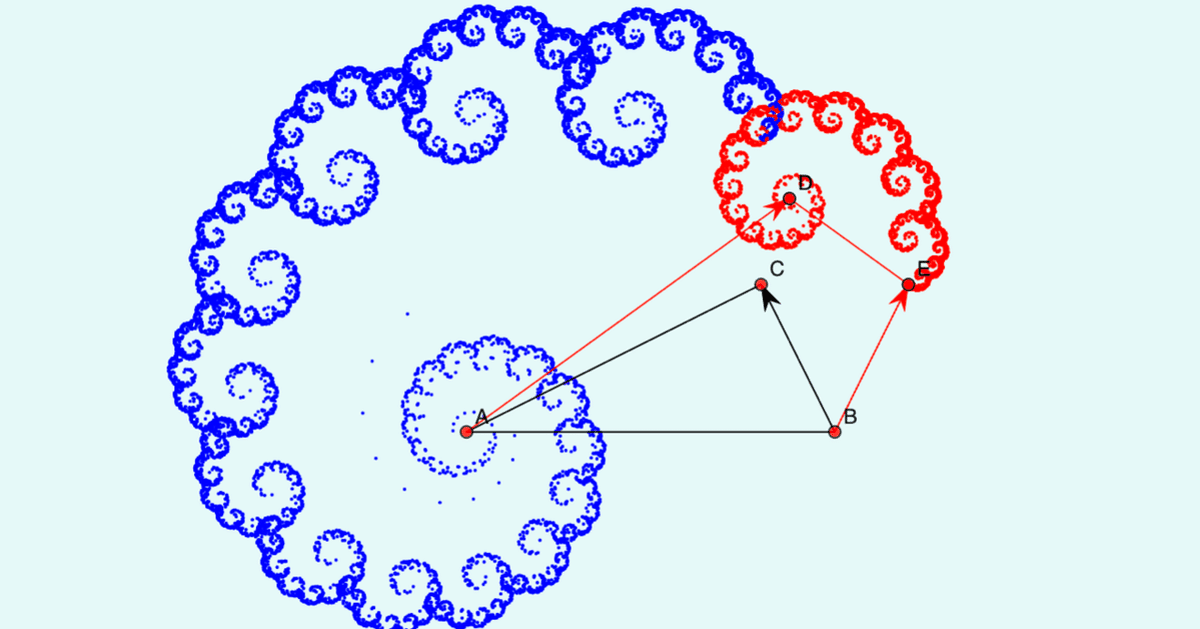
インドラの真珠:確率の役割
前節「反復関数系による極限集合の生成」では極限集合を作るとき、2つの変換からランダムに選ぶようにしました。「ランダムに選ぶ」ということは、「同じ確率で選ぶ」と言い換えてもよいでしょう。もしも「変換して点を打つ」という手続きが無限回行われるならば、この前提は問題にはなりません。極限集合のどの点の近くにも必ず点が打たれるでしょう。しかし、実際にはそうではありません。有限回でできるだけ極限集合に近いものを描かなければならないからです。すると,変換を選ぶ確率が変わると結果が変わってきます。
リンク先を開くと次のような図が出ます。
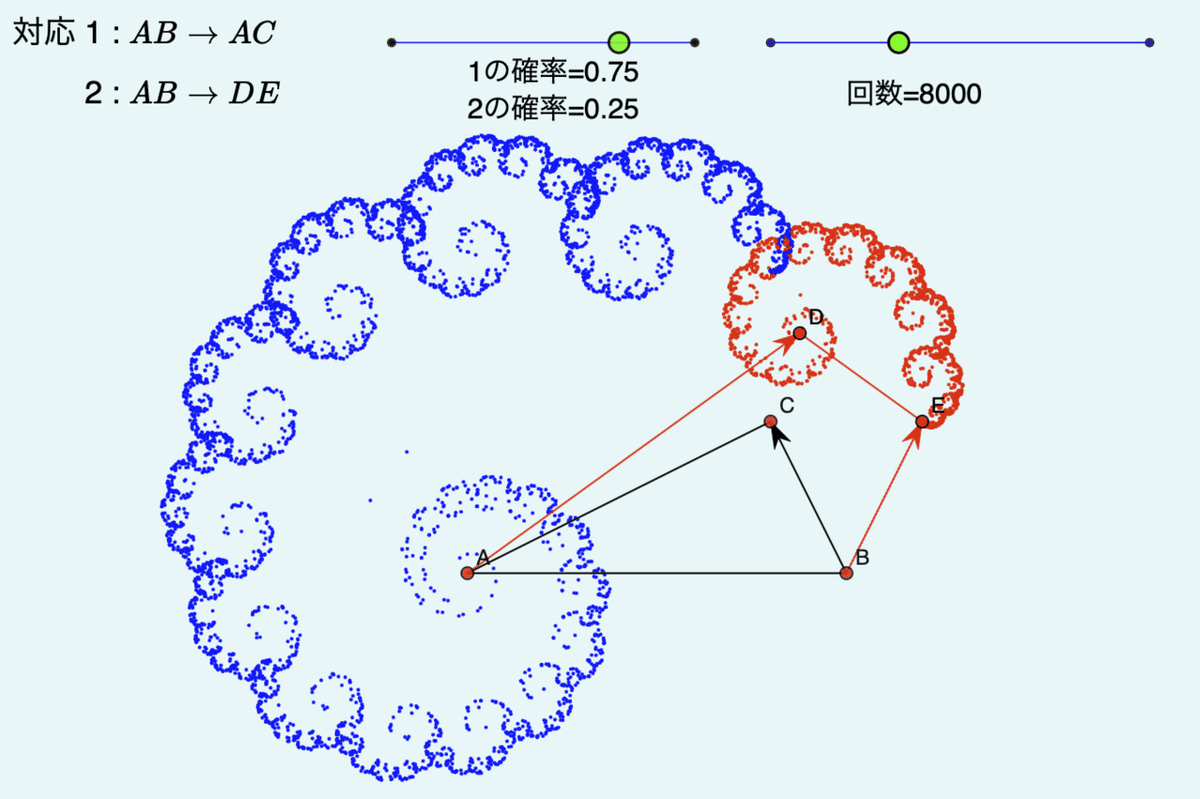
反復関数系は2つの相似変換で作られます。ひとつはABをACに対応させます(青の変換)。2番目はABをDEに対応させます(赤の変換)。上のスライダはそれぞれの変換が選ばれる確率を変えることができます。
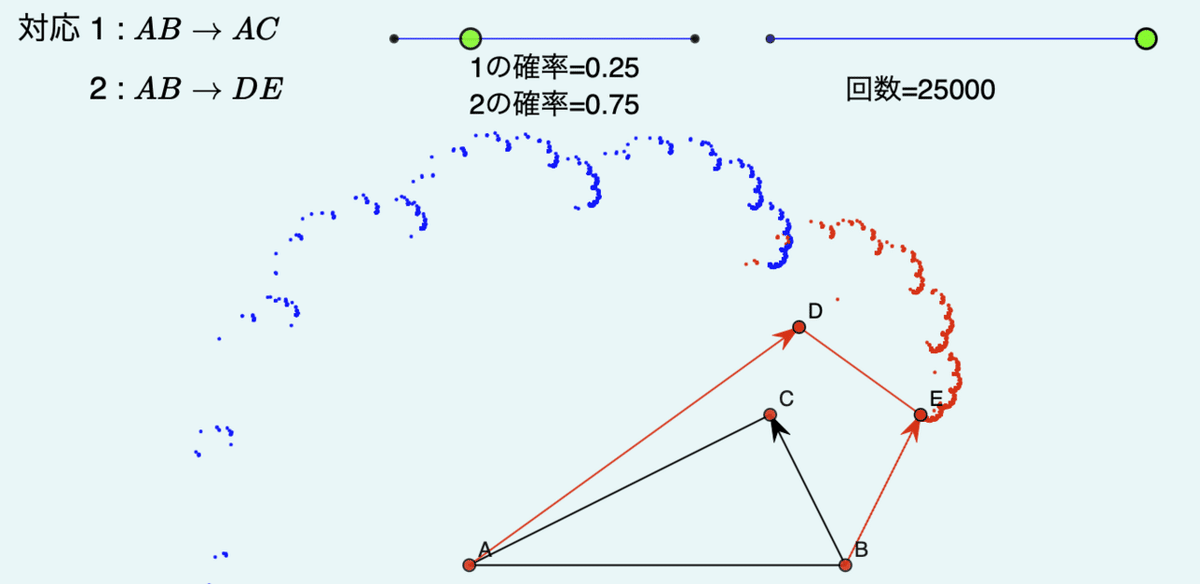
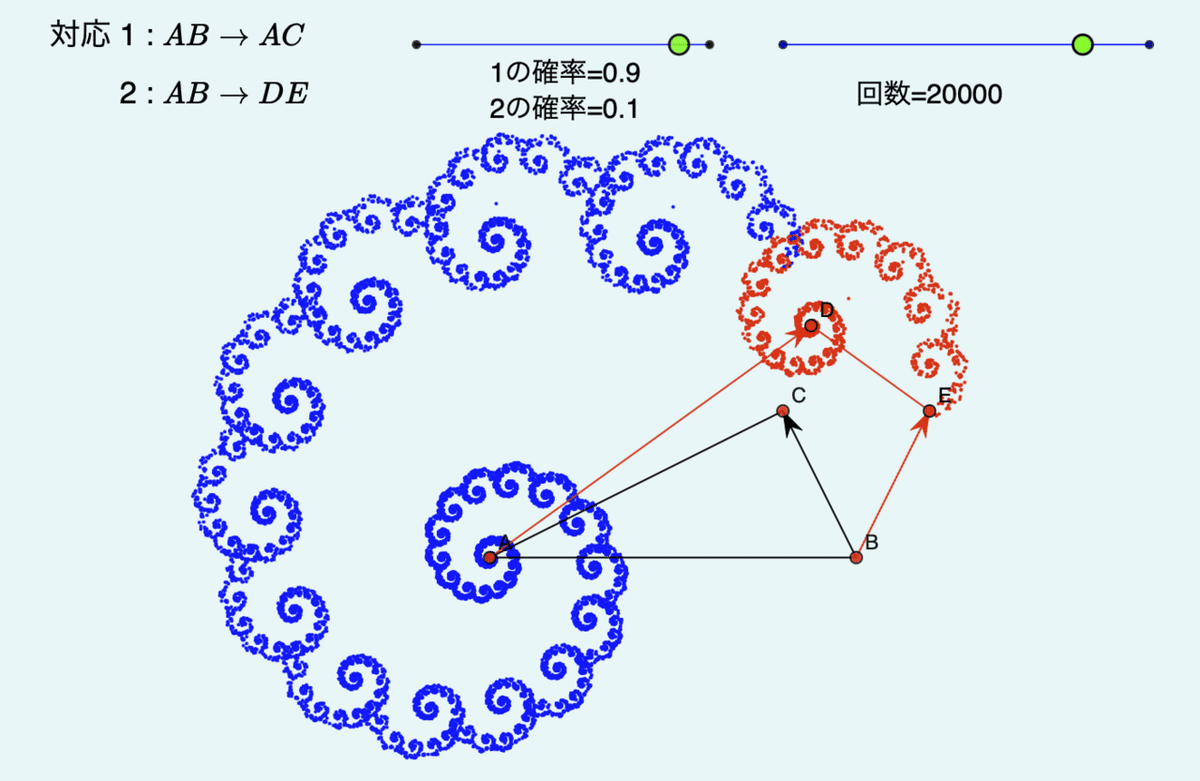
赤の確率が大きくなるとどうなるか、青の確率が大きくなるとどうなるか、またC,D,Eの位置を変えて変換の定義も変えていろいろ実験してみるのがよいでしょう。右上の回数スライダで回数を多くすると図が密になりますが,その分描画に時間がかかるため点を動かしたときの反応が遅くなります。

2つのメビウス変換を使ったものもやってみましょう。
リンク先を開くと次の画面になります。

確率のスライダを動かしてみましょう。
------------------------------------------
ここから先は,Cinderellaを使って,この実験を簡単に行う方法を説明します。
まず,5つの点A,B,C,D,Eを作図ツールでとります。
2つの相似変換を定義します。モードメニューの「変換」から「相似変換」を選び,まず A→A,B→C とします。右上に変換ボタンができます。
次に,A→D,B→E とします。次の図が,A→D の次に B→E を指定しているところです。
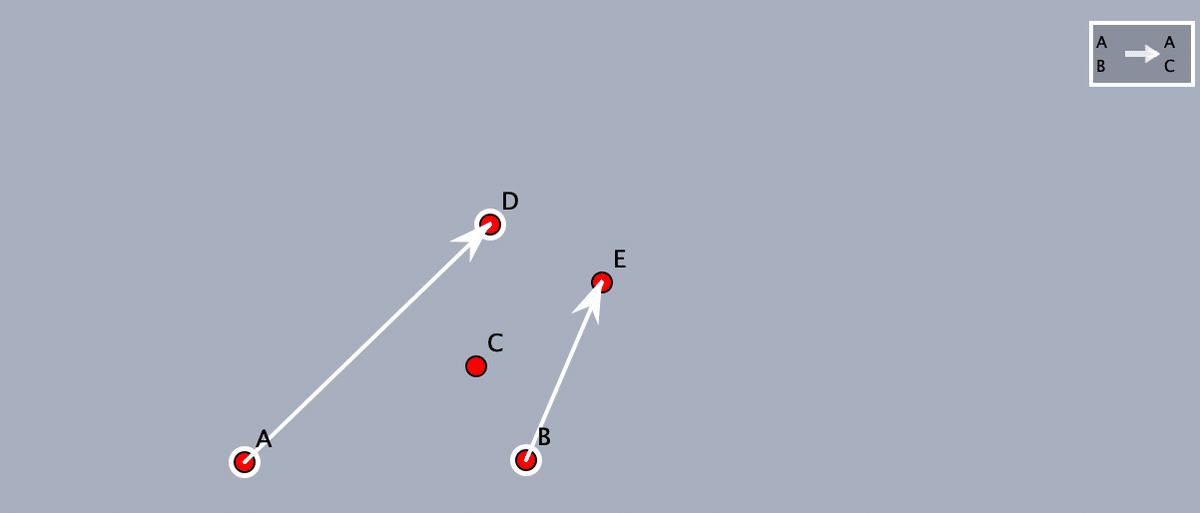
右上に2つ目の変換ボタンができます。
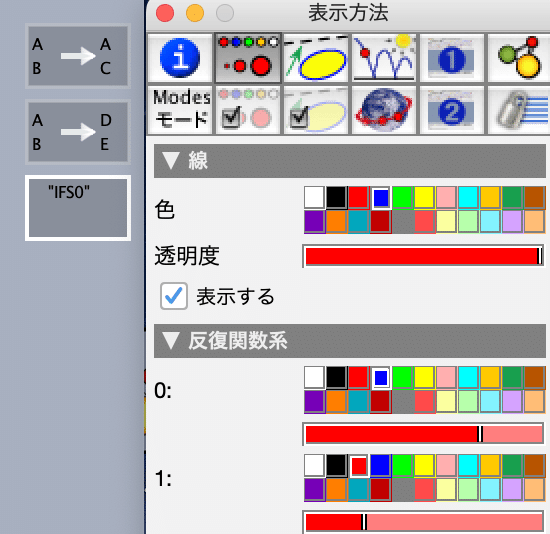
「要素を動かす」ツールボタンで動かすモードにして,シフトキーを押しながら,2つの変換ボタンを順にクリックして選択し,モードメニューの「特別」から「特別/反復関数系(IFS)」を選びます。

これで,2つの変換を用いた極限集合が描かれます。

スクリプトメニューからCindyScriptを選んでスクリプトエディタを開き,Drawスロットに次のコードを書きます。ここからコピーしてもよいです。
p1=0.75;
p2=1-p1;
IFS0.prob0=p1;
IFS0.prob1=p2;
E.x=E.x+0.0001;
E.x=E.x-0.0001;
drawtext((9,-2),"確率",color->(0,0,0),size->16);
drawtext((9,-3),"$p_1$="+p1,color->(0,0,1),size->16);
drawtext((9,-4),"$p_2$="+p2,color->(1,0,0),size->16);Shift+Enter で実行すると次のような図が出ます。(点A〜Eの位置によって図は変わります。)p1の値を変えると2つの変換を選ぶ確率が指定され,図が変化します。

また,はじめは表示されているのが黒と赤ですが,インスペクタを使うと色を変えることができます。右上の「IFS0」ボタンを選択し,Ctrl+I(⌘+I)または,編集メニューから「インスペクタ」を選んでインスペクタを表示し,色を変えます。

なお,スクリプトの中の E.x=E.x+0.0001; E.x=E.x-0.0001; の2行が奇妙に思われるかもしれません。これがないと,確率を変えて実行してもすぐには図が変わりません。これは,CindyScriptのスクリプトの実行タイミングによるもので,この2行がなくても実行後,どれかの点をクリックすれば図が変わります。
なお,こうして作った図をファイルメニューからHTMLに描き出しても動きません。CindyJSがIFSツールをサポートしていないからです。そのため,これとは別にプログラムを書いたものをWebに載せています。
→インドラの真珠:目次 に戻る
