インドラの真珠：共役複素数

複素数 $${a+bi}$$ に対し、$${a−bi}$$ を共役な複素数といいます。
$${a+bi}$$ を$${z}$$ で表したとき，$${a−bi}$$ は$${\overline{z}}$$で表します。
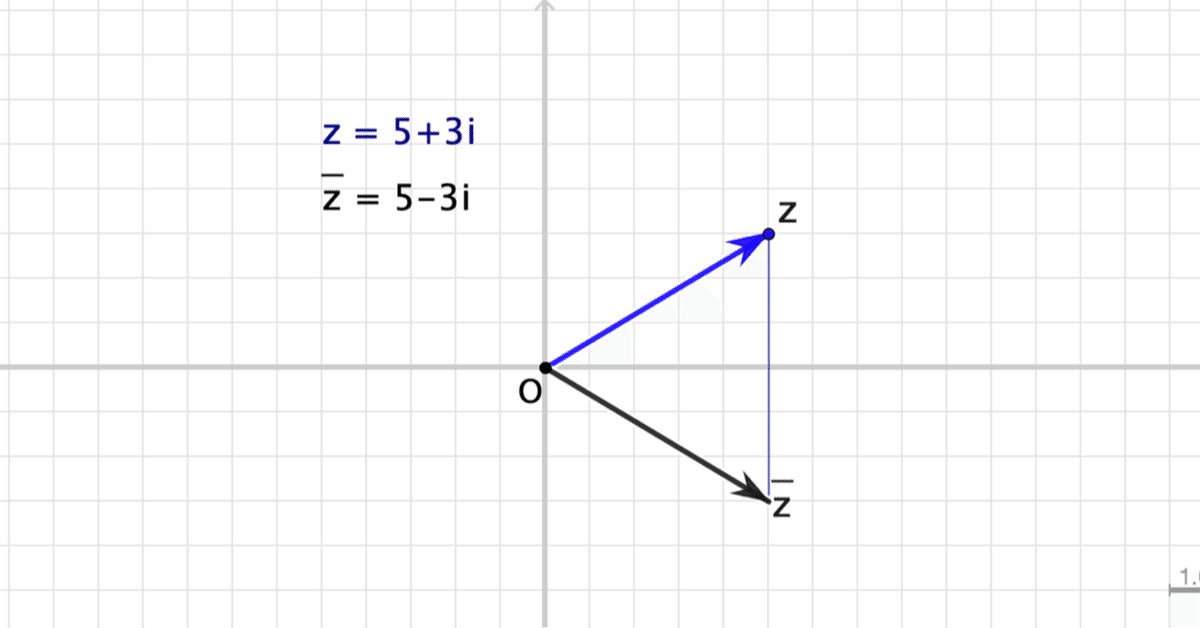
複素平面上では実軸に関して対称です。このことは、インドラの真珠で重要なキーワードである「対称性」と大きな関係があることを示しています。

共役複素数

リンク先を開くと，見出し画像にある画面になります。青いベクトルの終点をドラッグしてみましょう。

$${z}$$ と $${\overline{z}}$$ が実軸に関して対称であることが実感できるでしょう。

======================

ここからは，Cinderellaで共役複素数を扱う方法を説明します。

作図ツールの「点を加える」で点Aを適当なところにとります。点が取れたら「要素を動かす」ツールで選択モードに戻しておきます。画面下の磁石ツールで「グリッドにスナップする」にしておきましょう。

スクリプトメニューからCindyScriptを選んでスクリプトエディタの画面を出し，Drawスロットを選択して，次のコードを書きます。

z=complex(A.xy);
draw(gauss(conjugate(z)));

複素数 z に対して，共役複素数は conjugate(z) で表されます。
まず，点Aのxy座標を complex(A.xy) で複素数に変換し，conjugate(z) をgauss() でxy座標に変換して draw() で点を打ちます。
緑の点がAの共役複素数を表します。

→次節：複素数の累乗

→　インドラの真珠：目次　に戻る