
Cinderellaで数学:いろいろな曲線:連結クランクによる4次曲線
「曲線の事典」(礒田正美他・共立出版2009)に掲載されている,連結クランクのシステムによる4次曲線を描きます。
平面上に直線 s とその直線上に固定点Oが与えられている。点Pは点Oを中心とする円周上の点,点Aは線分PA=bの端点であり直線 s 上を動く。線分APを延長した線上の任意の点Qおよび,直線 PAに垂直な直線上に点Rをとる。点Pが点Oを中心とする円周上を動くとき,点Qのおよび点Rは4次曲線をかく。

Web上には次の写真があります。
Webの写真と図は左右が逆のようです。本の図は左右は同じですが,点Qの位置が写真と図とで異なっています。そのため,軌跡の位置も異なります。
ひとまず,図の方に従ってCinderellaで描きましょう。
まずx軸と原点を,直線ツールと点を加えるツールでとります。y軸は不要でしょう。次に原点を中心とする円を描き,円周上に点を取ります。これが動点Pになりますが,作図上の名前はDになるでしょう。
Dを中心とする大きな円を描き,x軸の直線との交点を取り(E)DとEを直線で結びます。
次に,点Q,R作図するために,Dを中心とする同心円を2つ描き,今の直線との交点をDの右側に取ります(F,G)。この F がQになります。
Gを中心とした円描き,Gを通る垂線を描いて交点を取ります(H)。
これで必要な点は取りました。点C(原点)とDは線分で結んでおきましょう。

インスペクタを開いて,点の名前(識別名)を次のように変えます。
C → O, D → P, F → Q, H → R
軌跡ツールを選び,動かす点としてP,軌跡を描く点としてQを選ぶと軌跡が描かれます。もうひとつ,軌跡を描く点としてRを選びます。

点の位置を決めるのにつかった補助円の大きさを変える軌跡の位置と形も変わります。うまくいったら,補助円を非表示にするなどして体裁を整えましょう。

この図をWeb上で動かすためには,軌跡は表示されないので関数でplotする必要があります。Qの方程式についての解説は曲線の事典に載っていますが,Rについては「Qの軌跡をアフィン変換したものである」としか書かれていません。
しかし,CindyScriptを使えば,方程式がわからなくても点Q,Rの位置を何らかの変数(媒介変数)で表すことができれば曲線をプロットできます。次はその一例です。
それぞれの線分の長さと角の大きさを下図のように変数で表します。

Pからx軸に下した垂線の長さは r1 sin t で表せるので,これを使って 角th は sinの逆関数 arcsin をつかえば t で表されます。
あとはPを基準にQ,Rの位置を表してから OP の分だけ平行移動すればいいわけです。スクリプトは次のようになります。
r1 = |O, P|;
r2 = |A, P|;
r3 = |P, Q|;
r4 = |P, G|;
r5 = |G, R|;
fq(t):=(
th = arcsin(r1*sin(t)/r2);
r1*[cos(t), sin(t)] + r3*[cos(th),sin(th)];
);
fr(t):=(
th = arcsin(r1*sin(t)/r2);
r1*[cos(t), sin(t)] + r4*[cos(th),sin(th)] + r5*[cos(th + pi/2), sin(th + pi/2)];
);
plot(fq(t), start -> 0, stop -> 2*pi, steps -> 500, color -> [1,0,0]);
plot(fr(t), start -> 0, stop -> 2*pi, steps -> 500, color -> [1,0,0]);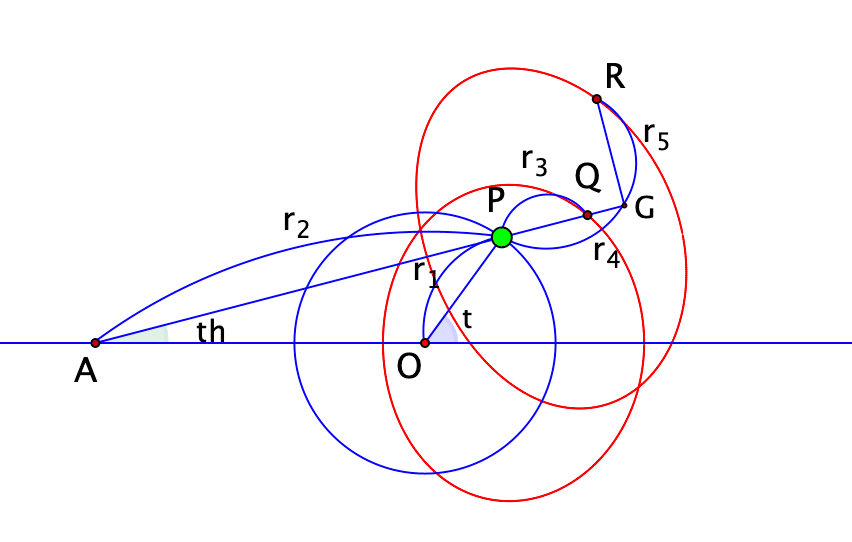
さて,前述のように,作図器の点Q,R の位置はこれとは異なります。実際には,$${r_3}$$ の長さが違うだけです。線などを加えて,作図器を模したものを作りました。
リンク先を開くと,タイトル画面のような画面になります。
←Cinderellaで数学・情報:記事一覧 にもどる
