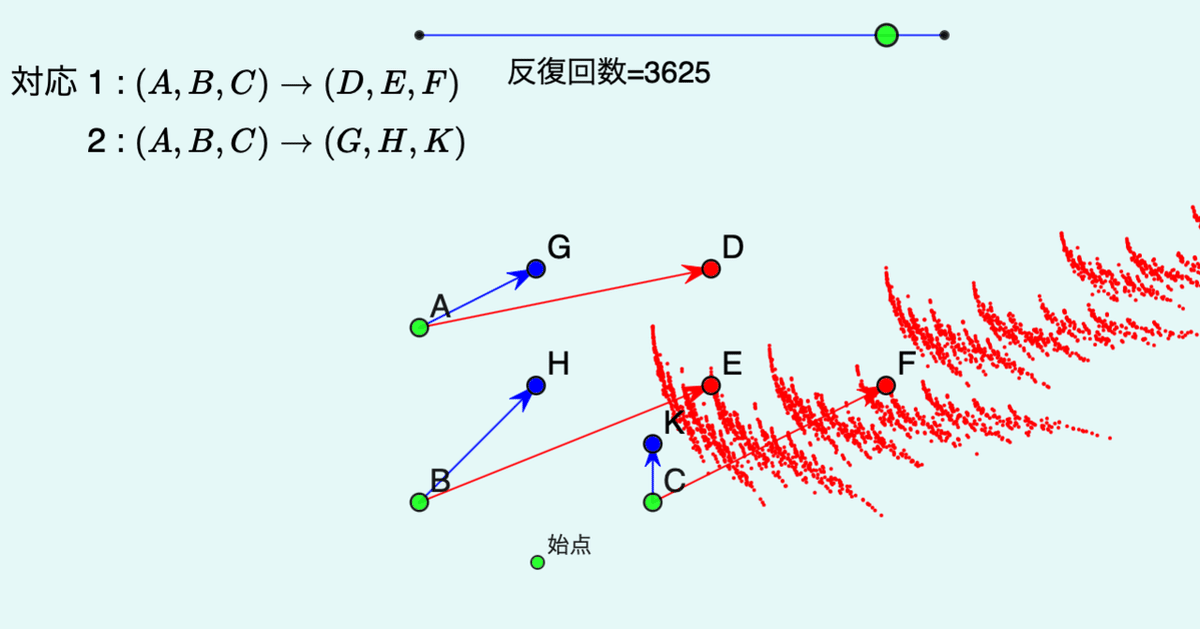
インドラの真珠:2つのアフィン変換と極限集合
回転、拡大・縮小に平行移動を加えたものをアフィン変換といいます。前の節では2つの相似変換に対して極限集合を描きましたが、これをアフィン変換にするとどんな図形が描かれるでしょうか。
Cinderellaでは,3つの点の組を対応させることでアフィン変換を定義します。これらの点を移動するとインタラクティブに定義を変えることができるわけです。
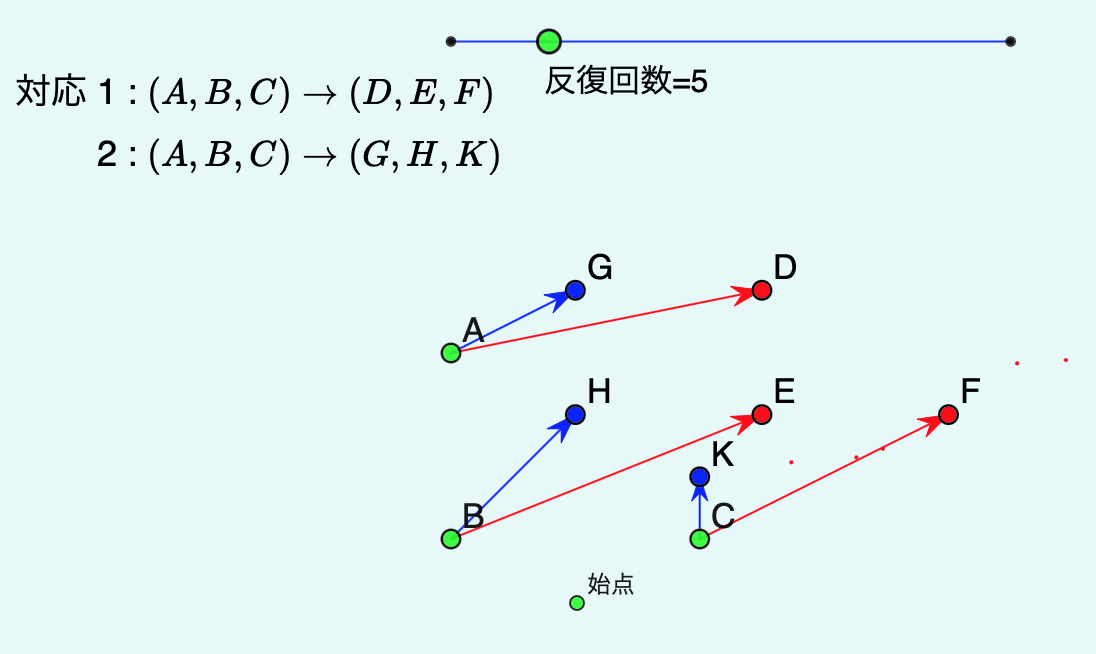
ます,上のスライダで反復回数を増やしてみましょう。
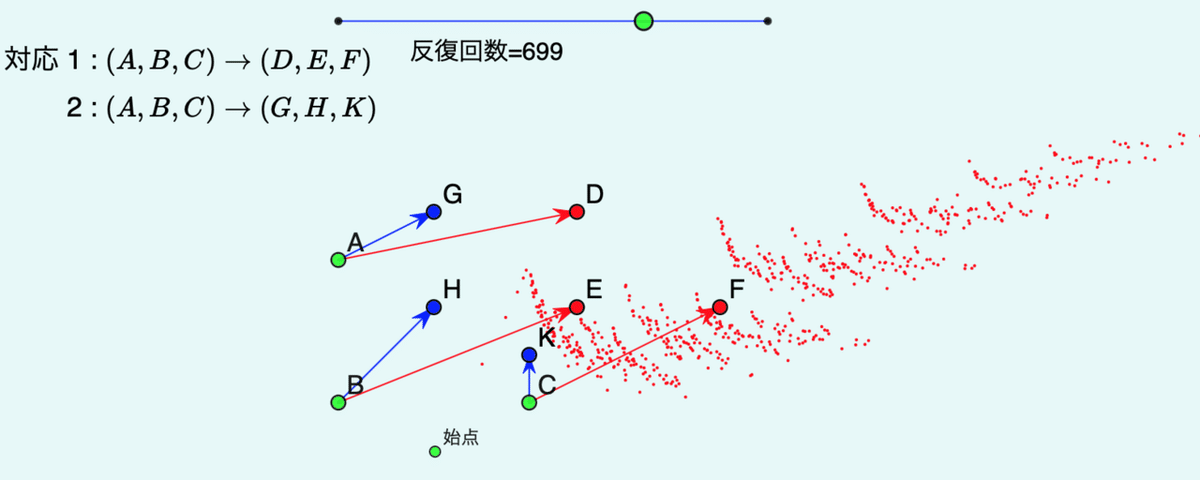
A〜Fの点の位置を変えると図が変わります。

始点は,もとになる点で,この点をまず変換し,変換先の点をまた変換し,と繰り返しています。2つのアフィン変換のどちらを選ぶかは,ランダムに決めています。
一見,なんの面白みもない図ですが,フラクタルのひとつとして有名な「バーンズリーのシダ」はこのアフィン変換を使って作られるのです。それを次の節で紹介しましょう。
Cinderellaには,プログラムを書かなくてもインタラクティブにアフィン変換を定義するツールがあり,それを繰り返す反復関数系のツールも用意されています。ただし,それで作図したものはWeb上で動かすことができません。それで,上のものはプログラムを書いています。CindyScriptには,点の対応を引数としてアフィン変換の行列を返す関数が用意されているのでそれを使っています。それほど難しいプログラムにはならないので紹介しておきましょう。
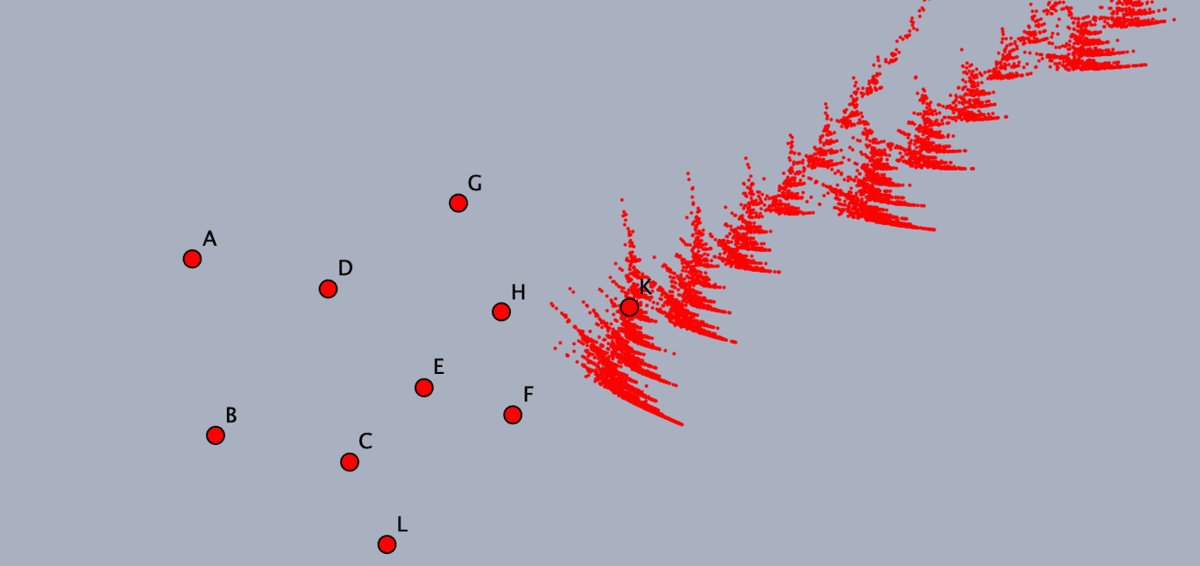
まず,A〜Lの10個の点をとっておきます。点の名前は自動的に付けられますが,IとJはスキップされます。
スクリプトエディタを開いて次のスクリプトを実行します。
n=10000;
z=complex(L);
// A,B,C→D,E,F
ga(z):=complex(map(A,B,C,D,E,F)*[gauss(z).x,gauss(z).y,1]);
// A,B,C→G,H,K
gb(z):=complex(map(A,B,C,G,H,K)*[gauss(z).x,gauss(z).y,1]);
repeat(n,s,
if(randominteger(2)==0,
z=ga(z);
,
z=gb(z);
);
draw(gauss(z),size->1,border->false,color->(1,0,0));
);
-----------------------
これはプログラムで描画しているので,ファイルメニューからHTMLに書き出せばCindyJSでWeb上で動かすことができます。
ここからは,プログラムを書かずに,Cinderellaでこの図を作る方法を説明します。
Cinderellaでは、3組の点の対応によりアフィン変換が定義できます。
まず、折れた釘のような線分を3組作ります。(実際には線分は使わないので,点をとるだけでもよいのですが,対応を分かりやすくするために線分にしています。)
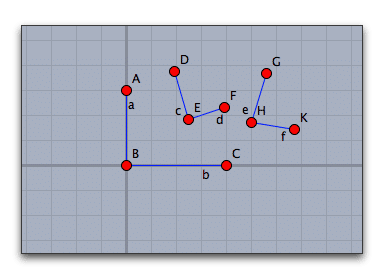
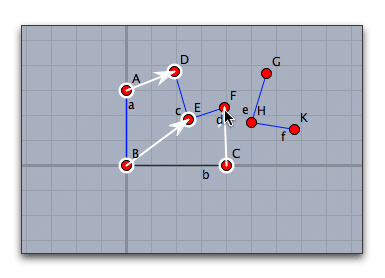
モードメニューから「変換」ー「アフィン変換」を選び、3つの組の対応を指定します。
もうひとつ、同じようにして、2つのアフィン変換を定義します。右上に、アフィン変換のアイコンが2つできます。
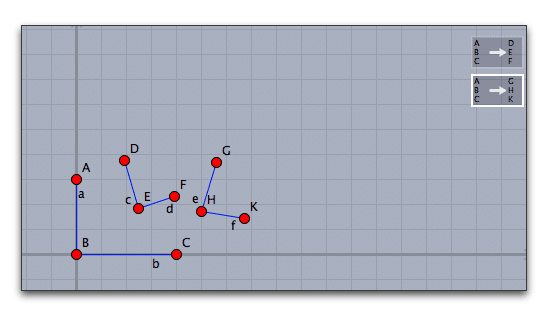
動かすモード(選択モード)にして、シフトキーを押しながら、2つのアフィン変換のアイコンをクリックして選び、特別メニューの「特別/反復関数系(IFS)」を選びます。これで極限集合が描かれます。
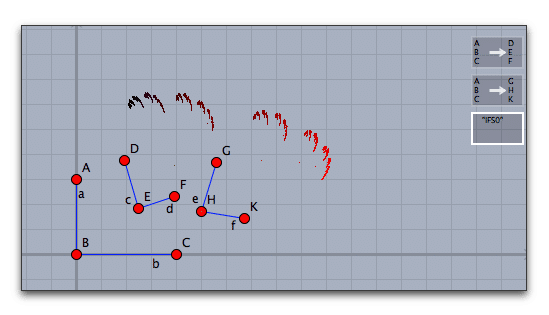
定義に使った点を動かしてみましょう。いろいろな極限集合が描かれます。なお,色付けは自動的に行われ,グラデーションがかかります。色を変えるには,IFSのツールボタンを選択して,インスペクタを開いて反復関数形の色を選択します。
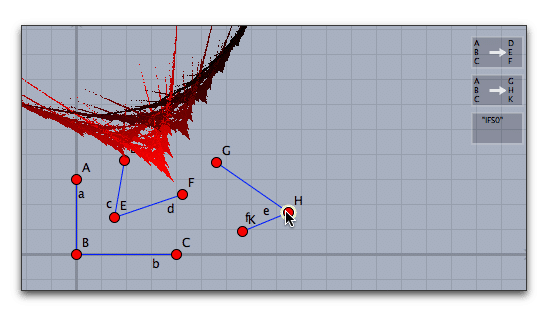
ただし,前述のように,CindyJSはIFSツールをサポートしていないので,この図をHTMLに書き出してもWeb上で動かすことはできません。
→次節:バーンズリーのシダ
