
Cinderellaで数学:いろいろな曲線:レムニスケート
この記事は,礒田正美他著の「曲線の事典」(共立出版 2009)に基づいています。
レムニスケートとは,「ペンダントのリボン」,「8の字」を意味するラテン語である。
レムニスケートの図は数学の参考書をはじめ,いろいろなものに掲載されています。Web上にもあり,方程式も載っていますので,ここでは,曲線の事典に出てくるものをCinderellaで描くことを主な目的としましょう。
描くのはベルヌーイのレムニスケートとGeronoのレムニスケートなどです。
ベルヌーイのレムニスケート
2点$${\rm{F}_1}$$と$${\rm{F}_2}$$ の距離が$${2a}$$ とする。点Pと点までの距離$${\rm{PF}_1}$$,$${\rm{PF}_2}$$ の積が $${a^2}$$ となる点Pの軌跡をベルヌーイのレムニスケートという。通常,レムニスケートといえばベルヌーイのレムニスケートを指し,4次曲線になる。
ベルヌーイの作図器
ベルヌーイは,レムニスケートを描くリンク機構の作図器を作っています。

これを模したものをCinderellaで作ってみました。
リンク先を開くと次の画面になります。

補助円は表示されていませんが,点DはAを中心として回転させることができます。それにリンクしてC,Mが動きます。ぐるっと回してMの動きを見てみましょう。「軌跡表示」ボタンをクリックするとレムニスケートが表示されます。

では,実際にCinderellaでこのリンク機構を作ってみましょう。
磁石ツールで座標軸と方眼を表示しておきます。まず線分ABをx軸上にとります。A,Bは原点を中心に左右対称な位置にします。Aを(-3, 0) に取ったとしましょう。AB=$${\sqrt{2}}$$AD とするために,Aを中心に,(0, 3) を通る円を描きます。不用意に半径が変わってしまわないように,「円を加える」ツールを使うのがよいでしょう。点C(0, 3) ができます。もう一つ,Bを中心にCを通る円を描きます。はじめの円周上に点Dをとれば,AB=$${\sqrt{2}}$$AD で,点Dを動かすことができます。(0, 3) の点Cは作図器のCとは異なりますので,インスペクタで適当に名前を変えておきましょう。

次に,AB=CDとなるように作図器の点Cを取ります。ABの長さをとるために,「コンパス」ツールを使います。最初の点としてA,二つ目の点としてBを選びます。白い円が描かれますが,これがコンパスで取った長さです。「コンパスの針を置く点」として,Dを選択しますと,Dを中心とする半径ABの円が描かれます。

この円と,Bを中心とする円の交点をとると,これが作図器のCになります。交点を求めるツールではなく,点を加えるツールで取るのがよいでしょう。

レムニスケートを描くのはCDの中点でしたので,CDを線分で結んでおいて,「中点を加える」ツールで中点をとります。点の名前はEになりますが,そのままでもいいし,インスペクタで名前をMにしてもよいです。
軌跡ツールを選び,「動かす点」としてDを選択します。動かす道はすでに指定されているので,軌道を描く点としてE(M)を選択しますと,レムニスケートが描かれます。

あとは補助円を非表示にしたり,AD,BCを結んだりしてリンク機構の図ができますが,これをファイルメニューの「HTMLに書き出す」でHTMLファイルを作っても,残念ながらCindyJS では軌跡は表示されません。先ほどのWebのリンク機構では,レムニスケートを描くのに,次の媒介変数表示の方程式を使っています。
$${x=\dfrac{\cos \theta}{(1+\sin ^2 \theta)}}$$
$${y=\dfrac{\sin \theta \cos \theta}{1+\sin ^2 \theta)}}$$
垂足曲線としてのレムニスケート
点Oを原点とする直交座標系で,$${x}$$軸上の点A,$${y}$$軸上の点BがOA・OB=$${4a^2}$$ を満たすように動くとき,直線ABは直角双曲線 $${xy=a^2}$$の包絡線である。
点Oから直線ABへ垂線の足Pを下ろすとき,点Pの軌跡はベルヌーイのレムニスケートとなる。
レムニスケートの描画は後半なので,これをCinderellaで描きます。
まず,直線を加えるツールで座標軸を描き,x軸上に点をとります。もうひとつ,適当なところに点を2つとります。こちらの点の位置はスクリプトで決めます。FとGになるでしょうから,EFを通る直線を描いておきます。原点にも点をとっておき,点Gと線分で結んでおきます。

点の名前を,先ほどの記述に合うように,インスペクタで変え,スクリプトエディタを開いて,Drawスロットにプログラムを書きます。
(1) 点Bの位置をOA・OB=$${4a^2}$$ を満たすように決める。
a の値は適当に決めて代入しておきます。
(2) 垂線の足Pの座標を求める。
A(p,0) , B(0,q) とすると,原点からABに下した垂線の足の座標は次のように求められます。
ABの方程式は$${y=-\dfrac{q}{p}(x-p}$$,垂線の方程式は$${y=\dfrac{p}{q}x}$$ なので,連立方程式を解いて $${x=\dfrac{pq^2}{p^2+q^2}}$$,$${y=\dfrac{p^2q}{p^2+q^2}}$$
これが,そのままレムニスケートの媒介変数表示になります。qは(1)の条件から,$${q=\dfrac{a^2}{p}}$$ようにpで決まりますので,関数形にするために,pを t で置き換えて式を作ります。
a = 2;
B.xy = [0, 4a^2/A.x];
fx(t):= t(4*a^2/t)^2/(t^2+(4*a^2/t)^2);
fy(t):= t^2*(4*a^2/t)/(t^2+(4*a^2/t)^2);
P.xy = [fx(A.x),fy(A.x)];
plot([fx(t),fy(t)], start -> 0.001, steps -> 500, color -> [1,0,0]);
plot([fx(t),fy(t)], start -> -100, stop -> 0.001, steps -> 500, color -> [1,0,0]);start -> 0.001 は分母が0になってしまうことのエラー対策です。したがって,厳密には原点を除いた図になります。

反転図形としてのレムニスケート
直角双曲線 $${xy=a^2}$$ が与えられている。この双曲線上を点Qが動くとき,OP・OQ=$${2a^2}$$ を満たす点Pの軌跡は,ベルヌーイのレムニスケートとなる。
このあとに図3.26 がありますが,実際にやってみると図と合いません。図に合わせて,「OP・OQ=$${4a^2}$$ を満たす点P」に修正して描きます。
OP・OQ=$${4a^2}$$ を満たす点Pは半径 $${2a}$$ の円に関するQの鏡像です。これを「反転(円に関する鏡像変換)」といいます。
作図するのは点A,Bと原点中心の円だけです。点の位置や円の半径はプログラムで決めますので適当にとっておきます。

スクリプトを書きます。
反転は複素数を用います。$${z}$$ に対して $${\dfrac{4a^2}{\overline{z}}}$$ とすればよいのです。
a = 2;
f(x):= a^2/x;
inv(p):=(
z1 = complex(p);
z2 = 4*a^2/conjugate(z1);
gauss(z2);
);
plot(f(x));
A.y = f(A.x);
B.xy = inv(A.xy);
C0.radius = 2a;
plot(inv([t,f(t)]), start -> 0.01, stop -> 100, color-> [1,0,0]);
plot(inv([t,f(t)]), start -> -100, stop -> -0.01, color-> [1,0,0]);
包絡線としてのレムニスケート
直角双曲線 $${xy=a^2}$$ が与えられている。この双曲線上の動点Qを中心,半径OQとする円による包絡線は,ベルヌーイのレムニスケートとなる。
こんどは作図ツールは使いません。スクリプトで直角双曲線を描き,repeat の繰り返しで円を多数描きます。
a = 2;
f(x):=a^2/x;
plot(f(x), color -> [0,0,0]);
dx = 0.1;
n = 30;
x = 1;
repeat(n,
drawcircle([x, f(x)],|[x,f(x)]|);
x = x + dx;
);
x = -1;
repeat(n,
drawcircle([x, f(x)],|[x,f(x)]|);
x = x - dx;
);
Gerono のレムニスケート
Gerono のレムニスケートは,媒介変数表示で
$${(x,y) = (\ cos \theta, \sin \theta \cos \theta}$$
で表されます。書き換えると
$${x = \ cos \theta, y= \dfrac{1}{2}\sin 2\theta }$$
なので,これはリサジュー曲線の一つです。
では,ベルヌーイのレムニスケートとどう違うか。係数を調整して描いてみました。
曲線の事典には,Geronoのレムニスケートの作図法も載っています。
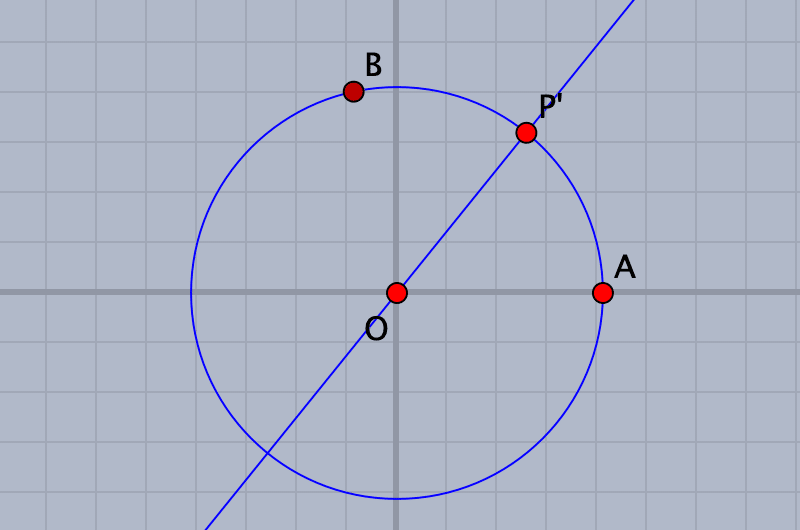
直交座標を考え,原点Oを中心,半径1の円をかき,円周上に点P'をとる。このとき,点P'の座標は $${(\cos \theta, \sin \theta)}$$ である。また,円と$${x}$$軸の交点をAとする。
直線OP'に関して,点Aを線対称変換した点Bの座標は $${(\cos 2\theta, \sin 2\theta)}$$ なので,点Pの座標を定めることができ,点P'を動かすときの点Pの軌跡は右の曲線になる。
「右の曲線」がレムニスケートですが,それを上の記述に従って作図しましょう。
まず円を描きます。半径1にすると小さいので(画面を拡大してもよいですが),半径4くらいにして,これを「半径1」と思うことにしましょう。
直線を加えるツールで,原点から円周上の適当なところに直線を引きます。また,円とx軸の交点(4,0)に点をとります。
「鏡映(対称)」ツールを選択し,鏡になるものとして線分ABを,鏡に映すものとして点Aを選びます。これで対称点Eができます。インスペクタで点の名前,またはラベルを変えておきましょう。
このあと,$${x = \ cos \theta, y= \dfrac{1}{2}\sin 2\theta }$$ となる点Pを取ります。スクリプトを書いてもよいですが,作図にこだわってみましょう。
まず,x座標は P' のx座標と同じなので,P'からx軸に垂線を下せば,P'はその上の点になります。垂線を下すために,A,Oを通る直線を引き,「垂線を加える」ツールで垂線を引きます。
次にy座標です。Bのy座標が $${\sin \2 theta}$$ なので,Bからx軸に垂線を下し,その足との中点をとれば $${\dfrac{1}{2}\sin \2 theta}$$ が作れます。

中点Gからx軸に平行な直線を引き,P'からの垂線との交点を取れば,これが点Pです。 作図順ではHですが,ラベルをPにしておきましょう。

P'をドラッグして動かしてみましょう。Pの軌跡を表示するために,軌跡ツールを選び,動かす点としてP',軌跡を描く点としてPを選択しますとレムニスケートが表示されます。

さて,こうして描いてみると,Gerono のレムニスケートとベルヌーイのレムニスケートは形状が違いますね。Gerono のレムニスケートは蝶ネクタイのような形です。
どのくらいの違いがあるのか,係数を調整して比較してみましょう。

